不同入流条件及偏航角下的单风机尾流特性
2024-05-24黄国庆刘廷林闫渤文莫蕊瑜邓晓蔚信志强
黄国庆 刘廷林 闫渤文 莫蕊瑜 邓晓蔚 信志强


DOI: 10.11835/j.issn.2096-6717.2022.019
基金項目:国家自然科学基金(51878104);外国专家重点支撑计划(zcsf2021008)
作者简介:黄国庆(1976- ),男,博士,教授,主要从事高层建筑、风机和输电线塔等结构抗风以及随机振动研究,E-mail:ghuang1001@gmail.com。
通信作者:闫渤文(通信作者),男,博士,副教授,E-mail:bowenyancq@cqu.edu.cn。
Received: 2021?11?30
Foundation items: National Natural Science Foundation of China (No. 51878104); Key Support Program of China for Foreign Experts (No. zcsf2021008)
Author brief: HUANG Guoqing (1976- ), PhD, professor, main research interests: wind resistance of tall building, wind turbine and transmission tower; random vibration, E-mail: ghuang1001@gmail.com.
corresponding author:YAN Bowen (corresponding author), PhD, associate professor, E-mail: bowenyancq@cqu.edu.cn.
(1. 重庆大学 土木工程学院,重庆 400045; 2. 中国船舶集团有限公司中船海装风电股份有限公司,重庆 401122; 3. 香港大学 土木工程系,香港 999077; 4. 河海大学 力学与材料学院,南京 211100)
摘要:随着大型风电基地建设,上游风机在运行时会使下游风场风速下降,湍流度增大,造成下游风机发电功率降低,加剧风机的疲劳破坏并缩短其服役周期。因此,亟需开展风机尾流研究,明确其特性及演化规律。为了揭示不同入流及偏航角下的单风机尾流特性,基于单风机尾流风洞试验,验证基于大涡模拟(Large Eddy Simulation, LES)结合致动线模型(Actuator Line Model, ALM)数值模拟方法的准确性;基于LES-ALM模拟方法研究入流风场(包括风速及湍流度)及偏航角对风机尾流特性的影响,阐明正负偏航角下单风机尾流的对称性。结果表明:随着背景湍流度的增大,风机尾流恢复速度加快;当入流条件相同时,风机设置正负对称偏航角,其尾流风速也表现出一定的对称性;风机偏航角越大,风机尾流膨胀宽度会逐渐减小,并降低尾流风速的亏损程度。
关键词:单风机尾流;偏航角;大涡模拟-致动线模型;来流条件
中图分类号:TK89 文献标志码:A 文章编号:2096-6717(2024)03-0115-09
Wake characteristics of single wind turbine under different inflow conditions and yaw angles
HUANG Guoqing1, LIU Tinglin1, YAN Bowen1, MO Ruiyu2, DENG Xiaowei3, XIN Zhiqiang4
(1. School of Civil Engineering, Chongqing University, Chongqing 400045, P. R. China; 2. CSSC Haizhuang Wind Power Co., Ltd., Chongqing 401122, P. R. China; 3. Department of Civil Engineering, The University of Hong Kong, Hong Kong 999077, P. R. China; 4. College of Mechanics and Materials, Hohai University, Nanjing 211100, P. R. China)
Abstract: With the rapid construction of large-scale wind farms, the upstream wind turbine will deteriorate the wind velocity in the wind turbine wake region and increase the wake turbulence, thereby reducing the power efficiency of the downstream wind turbine and aggravating the fatigue damage of the wind turbine to shorten its service life. Therefore, it is urgent to carry out the study of wind turbine wake characteristics. The main purpose of this study is to reveal the wake characteristics of a standalone wind turbine under different upstream flow conditions and with various yaw angles. Firstly, the accuracy of Large Eddy Simulation (LES) combined with Actuator Line Model (ALM) was verified by the corresponding wind tunnel test. And then, based on the LES-ALM simulation method, the effects of inlet (including velocity and turbulence intensity) and yaw angle on the turbine wake characteristics were studied, and the symmetry of the horizontal profiles of the wind turbine wake at the hub height was clarified with positive and negative yaw angles. The results show that with the increase of the background turbulence intensity, the recovery of the wind turbine wake will be accelerated. Moreover, under the same upstream flow conditions and symmetrical yaw angle, the certain symmetry of wind turbine wake velocity was also identified. When the yaw angle of the wind turbine increases, both the expansion rate of the turbine wake width and the deficit degree of the wake wind velocity would decrease.
Keywords: wind turbine wake; yaw angle; LES-ALM; upstream flow conditions
传统化石能源环境污染较大,且逐渐枯竭,亟须发展环境友好的清洁可再生能源。风能由于其商业化程度高,是全世界可再生能源开发的重点。在大型风电场中,上游风机在运行中会造成下游流场出现风速降低且湍流增加的尾流区域[1]。据统计,海上风电场中风机尾流引起的发电量损失达到10%~20%[2]。因此,对风机尾流特性的研究成为近年来风能领域的热点之一。
近年来,由于计算性能的大幅提升和计算流体力学(Computational Fluid Dynamics, CFD)方法的快速发展,基于数值仿真方法对风机尾流进行的研究越来越多[3-5]。Xie等[6]使用大涡模拟的方法研究了单台风机的尾流特性,他们发现尾流风速亏损在水平方向和垂直方向的上部保持自相似的高斯特性,在接近地面的尾流区域内无该特性。Vermeer等[7]研究了均匀来流下的风机近尾流特性,并研究了风机尾流在远尾流区域的衰减规律。Churchfield等[8]揭示了大气稳定性和地面粗糙度对风机响应、发电量以及尾流发展有显著影响。Na等[9]的研究表明,风机尾流干扰对下游风机的功率输出及风机载荷有较大影响。但目前系统开展不同来流风速及湍流度对尾流发展演化规律影响的研究相对较少。
风电场中通常使用尾流主动控制的方法减少尾流之间的相互影响。尾流主动控制的核心是通过上游风机的偏航以减少下游风机所在区域的风速亏损[10]。风机的偏航角越大,其尾流向侧边偏移的程度也就越大[11]。仿真研究表明,通过优化风电场的偏航角,两串列式风机的发电量至少可以提升5%[12]。Adaramola等[13]的研究也表明偏航控制在提高风电场的发电量上有巨大潜力。因此,研究不同偏航角对风机尾流发展的影響具有重要意义。
Dou等[14]通过风洞试验将偏航后的风机轮毂高度平面的远尾流(风机下游5倍风轮直径及以上位置处尾流)与基于高斯分布的尾流模型进行对比,发现两者符合程度较好。该结论可验证偏航后风机轮毂高度平面的远尾流同样符合高斯分布,证明偏航后的远尾流分布在统计上具有一定的对称性。而在实际工程中,下游风机一般处于上游风机的远尾流影响之中,且风机偏航包括正向偏航(风轮面逆时针旋转)和负向偏航(风轮面顺时针旋转),风机尾流也具有旋转性。在偏航与尾流旋转两个因素耦合作用下,正负对称偏航角下的远尾流是否具有对称性值得进一步研究。
笔者主要研究风机尾流在不同入流、不同湍流度和不同偏航角的情况下的发展规律,并探究风机在正负对称偏航时远尾流是否具有对称性。
1 数值方法
1.1 大涡模拟
大涡模拟根据不同涡旋的尺度对湍流中的涡分别进行处理,利用瞬时的N-S方程直接求解大尺度涡旋,而小尺度涡旋对大尺度涡旋的影响则是通过亚格子尺度模型来近似。结合实际情况,在不可压缩N-S方程中加入科里奥利力项以及浮力项来模拟地球自转效应以及由地表温度差异引起的垂向浮力。联立连续性方程得到的控制方程为 (2)
式中:Ⅰ为由地球自转引起的科里奥利力项;Ⅱ为压力修正项;Ⅲ为背景压力梯度项,作为推动风形成的驱动力;Ⅳ为应力张量项,其包括黏性应力和模化亚格子应力,本研究采用Smagorinsky亚格子模型[15],其表达式为 (3) (4)(5)
式中:为可解尺度湍流变形张量;为亚格子涡粘模型;为滤波尺寸;Smagorinsky常数取值0.14。式(2)中Ⅴ为浮力项;Ⅵ为风机叶片对流场的作用力源项,该项来自致动线模型。
1.2 致动线模型
数值仿真中,使用致动线模型代替风机。致动线模型最早由So?rensen等[16]提出。该模型思想在于将真实风机叶片沿径向离散,每个离散点用虚拟体积力代替。该方法不需要建立风机叶片实体模型,无需求解叶片表面边界层流动,大大降低了建模难度,提高了计算效率。致动线模型在模拟叶片旋转及捕捉叶尖与叶根的涡脱落具有较高精度。相关研究表明,致动线模型是除实体建模以外的一种精度较高的风机流场计算方法[17]。对于致动线模型中的每个致动点上的体积力,可以用叶素动量理论计算,其表达式为 (6) (7)
式中:为相对于叶素的空气流速;与分别为攻角对应的升力与阻力系数;为攻角;为半径位置处叶素弦长,为叶素宽度;为空气密度,取值1.225 kg/m3。 (8)
式中:为叶片的旋转角速度;和为轴向速度和切向速度。
2 数值方法验证
使用LES-ALM数值计算方法,为验证其计算准确性,将该方法计算结果与挪威科技大学(Norges Teknisk-Naturvitenskapelige Universitet, NTNU)研究团队开展的单风机尾流风洞试验的风速亏损结果[18]进行对比。
2.1 风洞试验与数值仿真参数设置
风洞试验[18]中的风洞长×宽×高为11.15 m×2.72 m×1.8 m。风机模型的翼型型号为S826,直径D为0.894 m,轮毂高度Hhub为0.817 m。风机模型的弦长与扭转角沿径向分布图以及风机的升阻力系数随攻角的变化如图1所示。试验中来流为均匀定常流,轮毂中心的参考风速=10 m/s,风机叶尖速比为6。对应在数值仿真中,设置长×宽×高为10 m×4.6 m×2 m的计算域,网格使用blockmesh生成,通过网格无关性验证,确保网格精度达到要求,计算域共960万网格。入流参数和风机参数与风洞试验保持一致,数值仿真中使用的边界条件如表1所示。
2.2 风洞试验与数值仿真对比验证
图2为数值仿真中计算的风速亏损与风洞试验测量的风速亏损值对比,从图中可以明显看出,在x/D=1、3位置处,数值仿真和风洞试验结果整体趋势符合较好,但是在轮毂中心位置处,数值仿真与风洞试验的结果有一定偏差,这是由致动线模型忽略轮毂对流场的影响造成的。而x/D=5位置距离风机较远,轮毂对该位置已无影响,从图中也可看出,无论是数值大小还是尾流趋势,数值仿真与风洞试验都符合较好。因此可认为LES-ALM方法能较好地计算风机尾流流场特征。
3 数值结果分析
3.1 入流生成与数值仿真基本参数
控制好入流特性是研究不同入流参数下风机尾流发展规律的前提。使用能较好控制入流特性的CDRFG(Consistent Discrete Random Flow Generation)方法[19]来生成入流,该方法是一种大涡模拟入口湍流生成方法[18]。研究中考虑由3种风速(Uh=6、10.4、15 m/s)和3种湍流度(I=2%、6%、10%)组合成的9种入流。
选用风轮直径D为152 m的5 MW风机,其基本参数如表2所示。上述入流生成方法虽然能较好地模拟出目标的脉动风速谱,并合理保持速度之间的相干性,但也具有一定的局限性。该方法生成的湍流风场能满足连续性方程,却较难满足动量方程。为使入流在计算域内能较好保持,避免出现湍流衰减过快现象,本研究将原型风机进行1:250缩尺,风机缩尺后参数如表2所示。足尺风机与同型号缩尺风机的尾流特性主要受雷诺数影响,研究中风机缩尺后的雷诺数为2×104,Chamorro等[20]的研究表明,该量级及以上的雷诺数对风机的远尾流特性的影响不大。因此,雷诺数对数值仿真结果影响较小,可利用缩尺后的风机进行尾流特性分析。
数值仿真中计算域的长×宽×高为8 m×2.4 m×1.8 m,其网格划分如图3所示,网格最大尺寸为0.05 m,最小尺寸为0.012 m。且该网格划分已通过无关性验证,最终网格数目达到587万。计算时间步长取入流风速跑过整个计算域所需时间的1/1 500。计算的所有工况如表3所示。
3.2 入流自保持性验证结果分析
将生成的入流在空风场(计算域中不加入致动线模型)中计算的风速和湍流度结果与目标设定值进行对比,验证入流的自保持性。图4、图5分别为不同工况轮毂中心位置处的平均风速![]() 和湍流度
和湍流度![]() 沿顺风向的变化图。从图4可知,风速的保持性较好,轮毂中心处的风速值基本稳定在目标值附近。从图5可知,2%和10%湍流度对应工况的湍流自保持性整体也较好,6%湍流度工况与目标湍流度的误差在±1%之内。因此,认为入流在计算域中的自保持性较好,可进行后续尾流流场计算。
沿顺风向的变化图。从图4可知,风速的保持性较好,轮毂中心处的风速值基本稳定在目标值附近。从图5可知,2%和10%湍流度对应工况的湍流自保持性整体也较好,6%湍流度工况与目标湍流度的误差在±1%之内。因此,认为入流在计算域中的自保持性较好,可进行后续尾流流场计算。
3.3 不同入流下风机尾流发展规律
在实际工程中,风机在无偏航状态下,尾流的发展主要受入流的影响。图6是入流风速和入流湍流度为6 m/s和2%、6 m/s和6%、6 m/s和10%、10.4 m/s和6%、15 m/s和6%下的单风机尾流轮毂高度平面风速归一化后的云图,云图所描述的物理量为平均风速归一化(![]() )后的結果。图7为对应工况的不同位置的风速归一化后的廓线。其中图6(a)、(b)、(c)与图7(a)、(b)、(c)为对比不同湍流度对风机尾流的影响,图6(b)、(d)、(e)为对比不同风速对风机尾流的影响。
)后的結果。图7为对应工况的不同位置的风速归一化后的廓线。其中图6(a)、(b)、(c)与图7(a)、(b)、(c)为对比不同湍流度对风机尾流的影响,图6(b)、(d)、(e)为对比不同风速对风机尾流的影响。
从图6可以看出,在风机后都存在一个风速减小的区域,并且随着离风机的位置越来越远,尾流风速与来流风速差距越小。而在图7中可以更加清晰地看出,距离风机越远,尾流的影响半径逐渐增大。这就是尾流风速的两个重要特征:随着与风机距离的增加,尾流风速会逐渐恢复为来流风速,并且尾流风速的膨胀半径会逐渐增加。从图6(a)、(b)、(c)和图7(a)、(b)、(c)可看出,随着入流湍流度的增加,尾流风速的亏损逐渐减小,尾流风速的恢复速度逐渐加快。从图6(b)、(d)、(e)和图7(b)、(d)、(e)可看出,在相同湍流度下,当入流风速小于额定风速时,尾流对风速变化不敏感。当风速大于额定风速时,即在风速为15 m/s时,风机后x/D=4位置处尾流的最低速度为来流风速的87.1%,并且不同位置的风速相差较小。因此,可认为在风速大于额定风速情况下,尾流风速恢复快。
3.4 正负对称偏航下尾流对称性分析
尾流的发展在风机偏航与尾流旋转两个因素的耦合作用下是否依然具有对称性,该问题值得研究。若对称性较好,则后续研究中只需研究正或负偏航工况或者即可。因LES-ALM数值方法没有考虑机舱与塔筒对风机尾流的影响,所以主要研究远尾流处轮毂高度平面尾流风速对称性。
以入流風速6 m/s和入流湍流度6%为例,研究单风机偏航角为±10°、±20°、±30°时对轮毂高度平面远尾流的对称性影响。图8为轮毂高度平面处经归一化处理之后的平均风速云图。从图8可以定性分析,风机在正负对称偏航情况下,其尾流也表现出一定的对称性。为更好地比较,图9给出不同对称偏航角下,风机后x/D=3~10位置处轮毂高度平面风速归一化后的廓线图,其横坐标的相邻刻度间距表示范围为![]() 0~1。图中对负偏航工况的风速廓线进行对称处理。负偏航风速廓线对称处理后的结果与正偏航的风速廓线相比,其尾流风速的数值大小及发展趋势都符合得很好。
0~1。图中对负偏航工况的风速廓线进行对称处理。负偏航风速廓线对称处理后的结果与正偏航的风速廓线相比,其尾流风速的数值大小及发展趋势都符合得很好。
上述现象在入流风速和入流湍流度分别为6 m/s和10%、10.4 m/s和2%以及10.4 m/s和6%条件下也较为明显。因此可得到结论,当来流情况相同时,单风机在正负对称偏航角下,其轮毂高度平面的远尾流处风速也表现出较好的对称性。
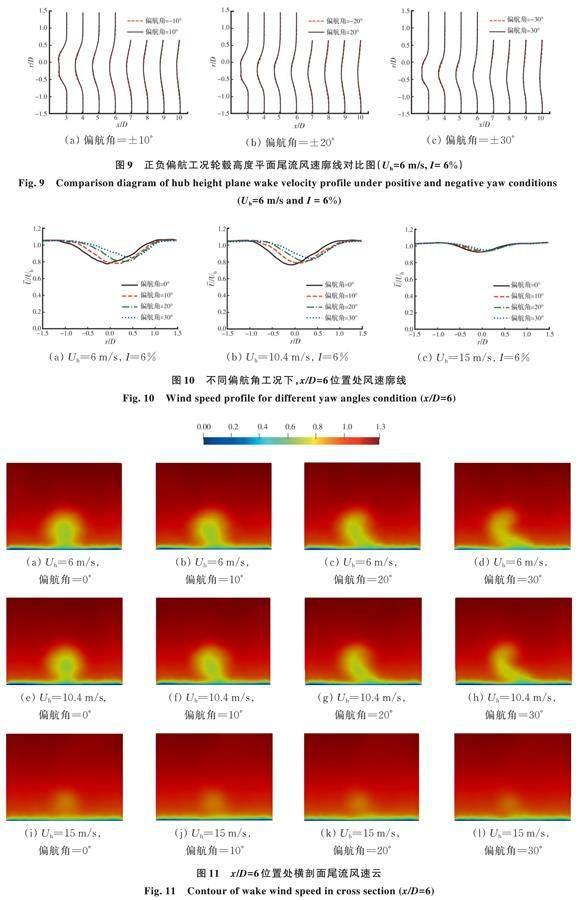
3.5 不同偏航角下风机尾流发展规律
偏航控制是工程中常用的减少上游风机尾流对下游风机影响的方法。单风机正负对称偏航下,其尾流发展也呈现较好的对称性,因此主要对比偏航角为10°、20°和30°与无偏航工况的尾流结果。图10(a)、(b)、(c)分别是入流风速和入流湍流度为6 m/s和6%、10.4 m/s和6%、15 m/s和6%条件下风机后6D位置处有无偏航的尾流风速廓线对比图。图11为对应工况x/D=6位置处的不同风速和不同偏航角下尾流风速云图。从图10、图11中可看出,单风机采用偏航控制后,尾流风速会向一侧偏移,尾流风速亏损的最大值减小,并且随着偏航角的增大,上述效果也越来越明显。当风速大于额定风速时,偏航对其尾流的影响会越来越小,尾流的偏转效应较为不明显。因此可得到结论:偏航会使尾流发生偏转,偏航角越大,尾流偏转程度越大。并且偏航后会使得尾流亏损幅值减小。随着风速增大,尾流的偏航效应会减弱。
4 结论
基于缩尺风机模型,使用LES-ALM方法研究不同入流风速、入流湍流度、不同偏航角条件下的单风机尾流特性规律。可得到以下结论:
1)来流为均匀定常流时,将LES-ALM方法计算尾流流场的结果与NTNU开展的风洞试验对比,符合情况较好,说明该方法能较好模拟均匀流下的流场特征。
2)利用CDRFG方法生成的入流风速及湍流度在基于LES-ALM方法的数值计算中具有较好的自保持性,从而为缩尺后风机的尾流数值仿真提供了支撑。
3)随着尾流的发展,距离风机越远处尾流的亏损越小,尾流风速的膨胀半径越大。当来流风速小于额定风速时,尾流发展对于风速较为不敏感,当来流风速大于额定风速时,风机的尾流效应相对较弱,尾流风速亏损较小。并且随着湍流度的增大,尾流的恢复速度越快,对应相同位置的速度亏损越小。
4)在同一入流下,单风机设置正负对称偏航后,其轮毂高度平面的远尾流处风速发展也呈现出较好的对称性,为简化计算工作量,后续在进行单风机尾流研究时,可只研究正偏航工况或者只研究负偏航工况即可。
5)当单风机设置主动偏航控制时,尾流会发生一定的偏转,尾流膨胀宽度会相对减小,且尾流亏损幅值低于同一入流下的无偏航工况。当风速小于额定风速时,偏航角越大,上述效应越明显。当风速大于额定风速时,由于尾流亏损本身较小,偏航后的尾流偏转效应较为不明显。
参考文献
[1] ARCHER C L, VASEL-BE-HAGH A, YAN C, et al. Review and evaluation of wake loss models for wind energy applications [J]. Applied Energy, 2018, 226: 1187-1207.
[2] BARTHELMIE R J, HANSEN K, FRANDSEN S T, et al. Modelling and measuring flow and wind turbine wakes in large wind farms offshore [J]. Wind Energy, 2009, 12(5): 431-444.
[3] IVANELL S, S?RENSEN J N, MIKKELSEN R, et al. Analysis of numerically generated wake structures [J]. Wind Energy, 2009, 12(1): 63-80.
[4] TROLDBORG N, S?RENSEN J N, MIKKELSEN R. Actuator line simulation of wake of wind turbine operating in turbulent inflow [J]. Journal of Physics: Conference Series, 2007, 75: 012063.
[5] WU Y T, PORTE-AGEL F. Large-eddy simulation of wind-turbin: Evaluation of turbine parametrisations [J]. Boundary-Layer Meteorology, 2011, 138: 345-366.
[6] XIE S B, ARCHER C. Self-similarity and turbulence characteristics of wind turbine wakes via large-eddy simulation [J]. Wind Energy, 2015, 18(10): 1815-1838.
[7] VERMEER L J, S?RENSEN J N, CRESPO A. Wind turbine wake aerodynamics [J]. Progress in Aerospace Sciences, 2003, 39(6/7): 467-510.
[8] CHURCHFIELD M J, LEE S, MICHALAKES J, et al. A numerical study of the effects of atmospheric and wake turbulence on wind turbine dynamics [J]. Journal of Turbulence, 2012, 13: N14.
[9] NA J S, KOO E, KO S C, et al. Stochastic characteristics for the vortical structure of a 5-MW wind turbine wake [J]. Renewable Energy, 2019, 133: 1220-1230.
[10] ARCHER C L, VASEL-BE-HAGH A. Wake steering via yaw control in multi-turbine wind farms: Recommendations based on large-eddy simulation [J]. Sustainable Energy Technologies and Assessments, 2019, 33: 34-43.
[11] BROMM M, ROTT A, BECK H, et al. Field investigation on the influence of yaw misalignment on the propagation of wind turbine wakes [J]. Wind Energy, 2018, 21(11): 1011-1028.
[12] AHMAD T, BASIT A, AHSAN M, et al. Implementation and analyses of yaw based coordinated control of wind farms [J]. Energies, 2019, 12(7): 1266.
[13] ADARAMOLA M S, KROGSTAD P ?. Experimental investigation of wake effects on wind turbine performance [J]. Renewable Energy, 2011, 36(8): 2078-2086.
[14] DOU B Z, QU T M, LEI L P, et al. Optimization of wind turbine yaw angles in a wind farm using a three-dimensional yawed wake model [J]. Energy, 2020, 209: 118415.
[15] GERMANO M, PIOMELLI U, MOIN P, et al. A dynamic subgrid-scale eddy viscosity model [J]. Physics of Fluids A: Fluid Dynamics, 1991, 3(7): 1760-1765.
[16] SO?RENSEN J N, SHEN W Z. Numerical modeling of wind turbine wakes [J]. Journal of Fluids Engineering, 2002, 124(2): 393-399.
[17] VRANA T K, FLYNN D, GOMEZ-LAZARO E, et al. Wind power within European grid codes: Evolution, status and outlook [J]. WIREs Energy and Environment, 2018, 7(3): e285.
[18] KROGSTAD P ?, ERIKSEN P E. “Blind test” calculations of the performance and wake development for a model wind turbine [J]. Renewable Energy, 2013, 50: 325-333.
[19] ABOSHOSHA H, ELSHAER A, BITSUAMLAK G T, et al. Consistent inflow turbulence generator for LES evaluation of wind-induced responses for tall buildings [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 142: 198-216.
[20] CHAMORRO L P, ARNDT R E A, SOTIROPOULOS F. Reynolds number dependence of turbulence statistics in the wake of wind turbines [J]. Wind Energy, 2012, 15(5): 733-742.
(編辑 王秀玲)
