仿木材料抗拉强度与应力-应变曲线试验研究

王安选,张华刚*,杨娇娇,吴小强,武绍元

(1．贵州大学 空间结构研究中心,贵州 贵阳 550025;2．贵州省结构工程重点实验室,贵州 贵阳 550025;3.中国水利水电第九工程局有限公司,贵州 贵阳 550081)

木材是一种天然可再生资源,是建筑文明发展史中人类早期认识和利用的建筑用材之一,木结构是我国古代建筑的主要结构形式之一,在唐朝就已形成较完整的营建方法,至北宋李诫主编《营造法式》后,古代木结构的应用技术已非常成熟[1]。木结构建筑具有能耗低、保温隔热、生态环保、空间利用率高等优点[2-5],但结构性能较多依赖于原生木材的性能,原生木材自然生长导致的构造不均匀会使木构件存在受力方向性问题[6],且易吸潮,存在防火和防腐性能差等明显缺陷[7-8],这些不利因素会限制木结构建筑的发展,同时,推广木结构会消耗大量有限的森林资源,而我国可用林资源又严重不足,因此,有必要研发一种新型建筑材料缓解资源和环境压力,为工程材料拓宽渠道。

氯氧镁水泥(magnesium oxychloride cement,MOC)是一种气硬性胶凝材料[9],是由MgO、MgCl2、H2O等反应而形成的三元复合相体系[10],具有高强度,强黏合力、耐磨、抗冲击、低碱性及低腐蚀性等优点[11],同时还具有良好的阻燃性和隔热性,目前已在市政、建筑、环保等产业及农业生产等众多行业中得到应用。当前,MOC及其制品技术已逐渐趋于成熟[12],有必要拓展其应用渠道。仿木材料是以MOC水泥为基体,再添加植物纤维和改性剂混合制成的无机胶凝材料,具有绿色环保、轻质高强、节能减耗等优点。刘艳君[13]、张鑫[14-15]等对仿木材料进行了相关研究,结果表明,由其制作的建筑结构构件,外观尺寸与混凝土构件大体相同,而其密度与常用木材相当,可大大降低结构自重,材料可用于建筑结构中。

仿木材料是脆性材料,抗拉性能是材料的重要力学性能。本文在已有研究基础上稳定材料配合比后,参考《混凝土物理力学性能试验方法标准》(GB/T 50081—2019)[16]来测定其轴心抗拉强度和应力-应变曲线关系,以期为后续研究及材料的工程应用提供参考。

1 材料与方法

1.1 试验材料的制备

本文的仿木材料在贵州省结构工程重点实验室自制完成。

1.1.1原料及压制模具

轻烧氧化镁和氯化镁为工业级,通过水合法测得轻烧氧化镁含量为59.98%,氯化镁含量为46%,水为自来水;植物纤维为市购细粒径木屑,粒径为5 mm左右;外加料柠檬酸、酒石酸和六偏磷酸钠等均为工业级,掺量按占活性氧化镁的质量比来计算[17]。

材料的压制模具系自行设计,如图1所示,主要由壁板、限位圆钢、压头等组成,可同时制作9个尺寸为220 mm×120 mm×150 mm的试件。

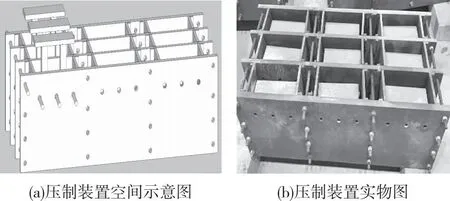
图1 压制装置图Fig.1 Pressing device diagram

1.1.2材料制备及试件制作

按配合比称量原料质量后,先将氧化镁和木屑放入图2(a)所示的搅拌机中搅拌20 min。同时将氯化镁、改性剂和水配置成卤水并搅拌15 min后,倒入搅拌机中与氯化镁和木屑材料再搅拌30 min,之后将混合料置于图1所示的压制模具中,然后将装料的压制装置对中放置在图2(b)所示的YEW-5000B全自动压力试验机平台上施压。由于混合料具有高压缩性,需再次投料后按密度控制法施压压实,随即通过限位圆钢锁紧模具后,将其从试验机上取下,室温下静置48 h后即可拆卸模具取出材料,再自然养护28 d即可。

图2 压制设备图Fig.2 Pressing equipment diagram

采用石材切割机,将制备的材料按图3制作成30个试件,用于轴心抗拉试验。应变通过粘贴在试件有效受拉区的A级应变片来采集。

图3 试验试件图Fig.3 Test specimen diagram

1.2 试验方法

参考《混凝土物理力学性能试验方法标准》(GB/T50081—2019)[16]进行试验。对试件进行表面处理,标注试验对中及轴心抗拉强度测试有效长度刻度线后,将试件严格对中放置在东华MTS-300KN微机控制电子万能试验机上夹紧后,按0.001 mm/s的速率匀速施加拉力直至试件拉断,数据用TST3828EN动静态型号测试分析系统采集,试验装置如图4所示。

图4 试验装置Fig.4 Test device

2 试验现象

随着轴拉荷载的不断增加,达到峰值荷载左右时,少数试件由于几何对中等原因,拉断面出现在有效受拉长度外,其余试件在有效受拉长度范围首先出现微小裂纹,直至试件断裂,呈脆性破坏,试件断裂面为锯齿状,断裂位置可拼接,试件破坏时,断裂面基本上与试件的长轴线垂直且不规则,其破坏形态如图5所示。仿木材料是由氯化镁、氧化镁、木屑和各改性剂以及孔隙、裂缝等结合在一起的复杂多相体系,断裂破坏本质上就是其微裂缝的形成和不断发展的结果。

图5 轴心抗拉试验试件的破坏形态Fig.5 Failure morphology of axial tensile test specimens

3 试验结果及分析

3.1 轴心抗拉力学性能

轴心抗拉强度和轴拉弹性模量是评价仿木材料力学性能的两个重要指标。参考《混凝土物理力学性能试验方法标准》,根据试件的荷载-位移曲线数据,材料的轴心抗拉强度按式(1)计算:

(1)

式中:ft为材料轴心抗拉强度,MPa;F为试件的破坏荷载(峰值荷载),N;A为试件的有效受拉截面面积,mm2。

根据应变测试结果,材料的轴拉弹性模量按式(2)计算:

(2)

式中:Et为材料的轴拉弹性模量,MPa;σ1/3为1/3的破坏应力,MPa;ε1/3为σ1/3所对应的应变值。

本文的30个测试试件中,共有5个试件的拉断面发生在有效受拉范围外,其余试件由实测有效受拉面积计算材料轴心抗拉强度测试值后,再求其强度平均值,当轴心抗拉强度测试值与平均值相差超过20%时,则舍去该测试值,将剩余结果的算术平均值作为材料的轴心抗拉强度。根据上述评定原则,共获得22个有效试验数据,如表1所示。参考《混凝土结构试验方法标准》(GB/T 50152—2012)[18]对试验结果的误差及统计分析,可见仿木材料的轴心抗拉强度最大值为9.33 MPa,最小值为6.40 MPa,平均值为7.98 MPa,标准差为0.97 MPa,变异系数为0.121,与文献[13]相比,本文的材料配合比使仿木材料的轴心抗拉强度提高了70%左右。仿木材料的轴拉弹性模量最大值为4 325 MPa,最小值为3 275 MPa,平均值为3 696 MPa,变异系数为0.089,为安全考虑,评定仿木材料的弹性模量Et=3 600 MPa。

表1 试验试件的力学性能测试结果Tab.1 Mechanical performance test results of test specimens

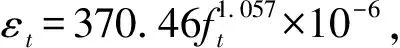
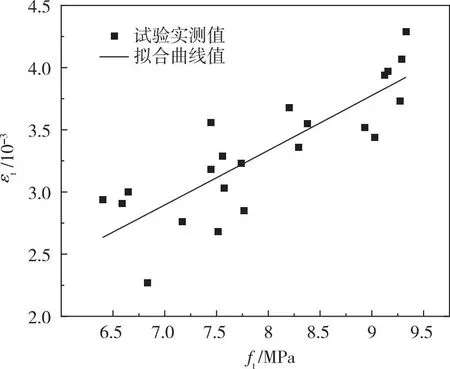
图6 抗拉峰值应力和峰值应变的关系Fig.6 Relationship between tensilepeak stress and peak strain

3.2 轴心受拉应力-应变曲线

以4号试件为例来描述材料的轴拉受力全过程,其实测应力-应变曲线如图7所示。可见,在轴心拉力作用下,材料的拉应变发展大致经历了4个阶段:

图7 4号试件实测应力-应变曲线图Fig.7 Measured stress-strain curve of specimen 4

(1)OA段,试验试件开始加载后经历轻微受拉,随即试件变形按一定的比例而增大,应力-应变曲线呈现直线态势,材料处于弹性受力状态,A点的拉应力为材料抗拉强度的60%左右。

(2)AB段,随着试验的缓慢加载,试件的应力-应变曲线开始逐渐偏离线性,呈现出非线性特征,曲线的斜率开始减小。拉应力逐渐增大,材料的应变增长梯度也相应变大,材料处于弹塑性受力状态。加载至B点时,形成一明显的尖峰,材料应力达到其最大抗拉强度,其值为7.76 MPa。

(3)BC段,材料在达到其最大抗拉强度后,即过峰值点B后,试件的承载力骤降,应力与之也很快下降,而应变增长缓慢,此时能用放大镜观察到试件表面存在的微小裂缝。

(4)CD段,随着加载的持续进行,试件中主要断裂面已经形成,表面出现肉眼可见的裂缝,应变增长加快,应力缓慢下降,裂缝迅速延伸和发展直至试件断裂,试件中其他部位未断裂的裂缝此时趋于稳定不再扩展。

本文22个有效试件实测的材料应力-应变曲线如图8所示,曲线在拉应力达到峰值即轴心抗拉强度ft前均为上凸曲线,曲线的下降段大部分皆呈现下凹态势,其脆性影响较为明显。

图8 试件实测应力-应变曲线Fig.8 Measured stress-strain curve of the specimen

3.3 轴心抗拉本构关系

目前,材料的本构关系曲线主要有单线型、双线型和分段型[20],本构关系函数主要有多项式[21],指数函数[22]等,各种本构模型均有其优缺点。根据测试结果,本文参考过镇海模型[19]来拟合仿木材料的轴心受拉的应力-应变关系。

3.3.1应力应变曲线归一化处理

按式(3)将全部测试结果做归一化处理,转化成无量纲变量:

(3)

得到的x-y曲线如图9所示,且满足:①x≥0时,1≥y≥0;②x=0时,y=0;③ 0≤x≤1,曲线呈上升态势;④x=1时,y=1,且dy/dx=0,曲线单峰;⑤x≥1时,曲线呈下降态势。

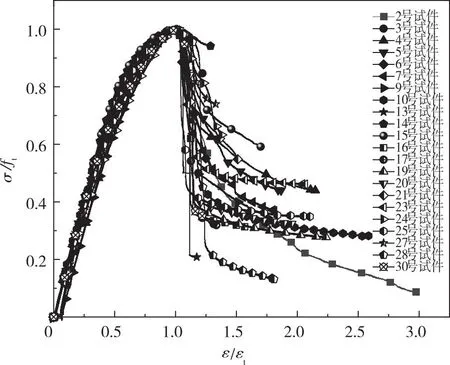
图9 轴心受拉应力-应变归一化曲线Fig.9 Normalization curve of axial tensile stress-strain

3.3.2本构关系拟合结果

根据曲线的形状特征,上升段曲线采用六次多项式(曲线区间为0≤x≤1),下降段曲线采用有理分式进行拟合(曲线区间为x≥1),函数关系如式(4)所示:

(4)

式中,a、b、c为待定参数。将本文的归一化数据代入,由最小二乘法解得参数a=1.710 88,拟合方差R=0.989 08;参数b=4.854 39、c=1.152 4,拟合方差R=0.750 07,可见曲线下降段的离散性较大。将上述参数代入式(4),可得仿木材料的本构关系为:

①当0≤x≤1时

y=1.710 88x-0.638 6x2-0.072 28x6

②当x≥1时

其拟合的本构关系曲线如图10所示。

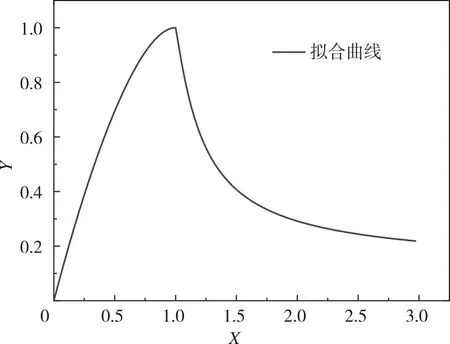
图10 本构关系拟合曲线Fig.10 Fitting curve of Constitutive equation

4 结论

1)仿木材料轴心受拉时,材料破坏呈脆性破坏,工程应用时应采取措施提高其延性。

2)根据本文的材料配合比,仿木材料的轴心抗拉强度平均值为7.98 MPa,变异系数为0.121;弹性模量为3 600 MPa。本文的配合比可供工程应用。

3)本文拟合的材料受拉本构关系,上升段拟合较好,而下降段离散性较大,更精准的材料本构关系拟合有待补充样本数量后才能获得。