基于集对分析-可变模糊集合的事故评价模型

2024-05-23郝佳奇詹淑慧

煤气与热力 2024年4期

徐鹏, 郝佳奇, 詹淑慧

(1.供热、供燃气、通风及空调工程北京市重点实验室, 北京 100044;2.北京建筑大学燃气研究中心, 北京 100044)

1 概述

近年来,全国燃气安全工作稳步推进,但燃气隐患的存在仍然导致大小事故的发生。对事故后果及原因进行客观准确的分析评价,是有效预防同类事故发生的必要手段。现有的事故研究多聚焦于燃气事故的预防措施及燃气事故的发生概率,对事故发生后的分析多为定性分析[1],定量分析还需进一步加强。当前燃气事故的统计与分析大多使用故障树分析(Failure Tree Analysis,FTA)进行引发事故原因的讨论[2],依据事件树分析(Event Tree Analysis,ETA)进行事故后果的讨论[3],都属于典型的演绎式分析方法。两种方法具有一定局限性,存在定量分析不足的情况。本文针对现有燃气事故评级具有模糊性的特点,提出集对分析与可变模糊集合耦合的方法对事故评级进行细节量化。

集对分析(Set Pair Analysis,SPA)是一种处理系统确定性与不确定性相互作用的数学理论[4]1-5,在事故风险分析、水资源预测和信息系统调节等诸多领域得到了广泛的应用[5-10]。其核心参数是联系度,用于描述随机、模糊、灰色等常见的不确定现象。可变模糊集合(Variable Fuzzy Set,VFS)理论是根据模糊概念的相对性及动态的可变性建立的,是对经典、静态模糊集合的突破与发展[11]201-203,其核心参数相对差异度的确定过程依赖经验[12-15]。以上两种理论的核心参数联系度与相对差异度本质上是一致的,将两种评价方法结合,通过构建集对分析的联系度反映可变模糊的差异度,可简化可变模糊差异度的构建过程,实现两种方法的优势互补。

指标的权重反映了指标在事件中的地位和作用,其确定方法可分为主观赋权法和客观赋权法。主观赋权法是根据专家经验确定各指标在问题事件中的地位和重要性,有层次分析法、最小平方法、环比评分法、二项系数法和专家调查法等[16]。客观赋权法是根据一定的规则对各指标自动赋权,而不依赖人的主观判断,主要有主成份分析法、熵权法(Entropy Evaluation Method,EEM)等[17-19]。通过确定信息的差异性[20-21],熵权法在对每一项指标的熵进行计算的基础上,对各个指标的权重进行计算,得到准确、可靠的指标权重[22]。

利用熵权法将评价指标权重量化,综合集对分析与可变模糊方法构建燃气事故评价模型,对事故后果评级进一步量化,有利于准确认识事故的严重程度,从而制定相应的风险应对措施。

2 理论基础

2.1 集对分析

集对分析方法首先是将具有一定联系的两个集合X与Y构建成集合对H=(X,Y),进而对集合对的特性进行同一、差异、对立的系统分析,通过联系度μ描述两个集合之间的关系,其定义式为[4]1-10:

μ=a+bi+cj

(1)

式中μ——两集合的联系度

a——两集合的同一度,即两集合中处于同一状态元素的个数与元素总个数的比值

b——两集合的差异度,即两集合中处于差异状态元素的个数与元素总个数的比值

i——差异度系数,表达不确定关系

c——两集合的对立度,即两集合中处于对立状态元素的个数与元素总个数的比值

j——对立度系数,表达反关系

a,b,c统称为联系度μ的联系分量,a,b,c∈[-1,1],且a,b,c满足归一化条件。i、j也称为联系分量b和c的取值系数。i∈[-1,1],j=-1。当i取值趋向于1时,对联系度起增益作用;当i取值趋向于-1时,对联系度起减益作用。

对两集合之间的差异和对立关系进一步细化,可表示为[23]:

μ=a+b1i++b2i-+c1j++c2j-

(2)

式中b1——集合中的元素处于与对应区间相邻区间的优越评价侧时的差异度

i+——优越评价区间差异度系数

b2——集合中的元素处于与对应区间相邻区间的劣差评价侧时的差异度

i-——劣差评价区间差异度系数

c1——集合中的元素处于与对应区间相隔区间的优越评价侧时的对立度

j+——优越评价区间对立度系数

c2——集合中的元素处于与对应区间相隔区间的劣差评价侧时的对立度

j-——劣差评价区间对立度系数

其中,各参数满足如下关系:

a+b1+b2+c1+c2=1

(3)

取值范围为:i+∈[0,1],i-∈[-1,0],j+∈{0,1},j-=-1。

2.2 可变模糊集合

(4)

式中D——u对吸引度A的相对差异度

ηA——u对吸引度A的相对隶属度

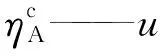
因此,具有吸引性质的相对隶属度可写为如下形式:

(5)

2.3 熵权法

对于具有各种属性的大量数据,如果所有数据的某个属性值都相同,则该属性就不具有区分不同数据的作用。对于各数据,某一属性的取值差异性越大,即离散度越高,其区分数据的意义也越大。

信息量的大小跟随机事件发生的概率有关。越小概率的事件发生,其产生的信息量越大;大概率事件的发生,产生的信息量小。信息熵(Information Entropy),就是平均而言一个事件的发生可以提供的信息量的大小。信息量度量的是一个具体事件发生了所带来的信息,而信息熵则是在结果出来之前对可能产生的信息量的数学期望——考虑随机变量的所有可能取值所带来的信息量的期望。熵权法是根据指标信息熵的大小对指标权重进行客观赋值的一种方法。信息熵小,代表该指标的离散程度大,包含的信息就多,所赋予的权重就大。

3 事故评价模型的建立

依据造成危害的严重程度和影响范围,通常将燃气事故划分为若干评级。建立基于集对分析-可变模糊集合的评价模型,可对燃气事故评价指标的评级进行量化,具体步骤如下。

① 构建燃气事故指标评级标准集合与事故指标评价值集合

定义集合X为事故指标评级标准集合,集合Y定义为事故指标评价值集合,分别表示如下:

(6)

Y=(y1,y2,…,yn)

(7)

式中xhn——第n个评价指标对应的评级标准

yn——第n个评价指标的评价值

② 确定集对联系度

燃气事故评级一般分为“很小、小、一般、大、很大”,共5级,即事故指标评级k的值可以为1,2,3,4,5。本文的事故评级为越小越优型,优越评价侧即为对应区间前的较小评级区间,劣差评价侧为对应区间后的较大评级区间。建立评价指标的评价值ym与事故指标评级k之间的单指标联系度μkm,以k=3为例,μ3m的计算式为[4]1-10:

(8)

式中μ3m——第m个评价指标的评价值ym与事故指标评级3之间的单指标联系度

x0m、x1m、x2m、x3m、x4m、x5m——第m个评价指标的第0、1、2、3、4、5个评价标准

ym——第m个评价指标的评价值

③ 确定相对隶属度

由集对分析的定义可知,μkm越接近1表示指标评价值与指标评级间的一致性越强。这与可变模糊集合理论中的相对差异度的内涵本质上一致,因此可以使用集对分析理论计算出的单指标联系度μkm作为可变模糊集合理论中的相对差异度D。因此,式(5)可写为如下形式[14]:

(9)

式中ηkm——第m个指标评价值对指标评级k的相对隶属度

μkm——第m个指标评价值对指标评级k的相对差异度(或单指标联系度)

④ 确定评价指标的权重

信息熵关注的是变量取值的多样性,取值大小差异越大,即离散程度越高,就说明重要程度大,包含了更多的信息。第m个评价指标的影响占全部指标影响的比例的计算式为:

(10)

式中pm——第m个评价指标的影响占全部指标影响的比例

km——第m个指标评级

n——评价指标总数

kt——第t个指标评级

第m个评价指标的信息熵em的计算式为[9]:

em=-pmlnpm

(11)

式中em——第m个评价指标的信息熵

按照此方法,计算出全部评价指标的信息熵。

信息熵越小,指标的离散程度越大,该指标对综合评价的影响(即权重)就越大。通过熵权法对各指标的权重进行计算[9]:

(12)

式中ωm——第m个评价指标的权重

et——第t个评价指标的信息熵

⑤ 计算综合隶属度

将n个指标中的q个指标合并为一个新的指标(称为合并指标),被合并的指标称为子指标。第t个子指标的编号记为s(t),例如将n个指标中的第1、2个指标合并,则s(1)=1,s(2)=2。合并指标对于指标评级k的综合隶属度Vk可通过其子指标的权重和相对隶属度计算,见下式[27]:

(13)

式中Vk——合并指标对指标评级k的综合隶属度

q——子指标的数量

ωs(t)——第t个子指标的权重

ηk s(t)——第t个子指标评价值对指标评级k的相对隶属度

β——可变距离参数

α——可变优化准则参数

α有两种取值[11]218-221,α=1时为最小一乘法准则,表示事故评价指标对于所有评级的加和最小;α=2时为最小二乘法准则,表示事故评价指标对于所有评级的差异最小。β有两种取值[11]218-221,β=1为海明距离(Hamming Distance),表示将事故评价指标及其所属评级转化为二进制的整数,统计二进制数中不同数字的个数;β=2为欧氏距离(Euclidean Distance),表示事故评价指标及其所属评级两个数值之间的差异。计算评价指标对指标评级k的综合隶属度时,需要引入可变优化准则参数α以及可变距离参数β的不同组合方式计算。进行不同的参数组合计算,是可变模糊方法的重要特点。当使用此方法对无子指标的案例进行分析时,公式(13)仍适用,不需合并指标进行逐一求和。计算获得的4组事故指标评价的综合隶属度Vk的平均值,可以得到满足归一化要求的综合隶属度V。

⑥ 确定修正后的合并指标评级

当各子指标评级不相等时,取q个子指标中较大的评级作为合并指标评级。考虑合并指标对指标评级的隶属度,对合并指标的指标评级进行修正,得到修正后的合并指标评级H,H以更量化的数据进一步反映燃气事故的影响程度。H的计算式为[27]:

H=kqV

(14)

式中H——修正后的合并指标评级

kq——合并指标评级

V——满足归一化要求的综合隶属度

4 实例分析

以呼和浩特“11·22”燃气爆炸事故为例,其事故原因是燃气管道发生环向断裂,导致燃气泄漏后达到爆炸极限发生爆燃[28]。这次燃气管道泄漏事故共造成1人死亡,14人受伤,直接经济损失约868×104元。按照DB11/T 1478—2017《生产经营单位安全生产风险评估规范》,仅考虑人员伤亡及直接经济损失,根据DB11/T 1478—2017规定的事故评级区间,构建事故指标评级标准集合X和指标评价值集合Y。

(15)

Y=(1,14,868)

(16)

在X中,第1行为人员死亡评级,当死亡人数数值(单位为人)属于[1,3)时评级为3,属于[3,10)时评级为4,大于等于10时评级为5。第2行为人员受伤评级,当受伤人数数值(单位为人)属于[0,3)时评级为1,属于[3,5)时评级为2,属于[5,16)时评级为3,属于[16,50)时评级为4,大于等于50时评级为5。第3行为经济损失评级,当经济损失数值(单位为元)属于[0,200×104)时评级为1,属于[200×104,1 000×104)时评级为2,属于[1 000×104,5 000×104)时评级为3,属于[5 000×104,10 000×104)时评级为4,大于等于10 000×104时评级为5。

① 计算指标联系度

根据集合X和Y确定各个事故评价指标的评级,由式(8)计算人员死亡、人员受伤评价指标与指标评级间的联系度。其中参数取值i+=0.5,i-=-0.5,j+=0,j-=-1。计算得到μ31=0.222,μ32=1。

② 计算相对隶属度

将得到的各指标联系度代入式(9),可计算出“人员死亡”和“人员受伤”评价指标隶属于评级3的相对隶属度分别为η31=0.611和η32=1。

③ 确定指标权重

由前文可知,人员死亡、人员受伤评价指标的评级均为3,经济损失评价指标的评级为2。根据式(10)可计算得出人员死亡评价指标的影响占全部指标影响的比例p1=0.375,同理可得p2=0.375,p3=0.25。代入式(11)中,可计算得出人员死亡评价指标的信息熵e1=0.368,同理可得e2=0.368,e3=0.347。进一步根据式(12)计算出人员死亡指标的权重ω1=0.330,同理可得人员受伤指标的权重ω2=0.330。

④ 计算综合隶属度及其平均值

根据DB11/T 1478—2017,人员受伤和人员死亡评价指标应合并为一个指标,即人员伤亡评价指标。对人员伤亡评价指标进行评级,通过其子指标人员受伤和人员死亡评价指标的权重ω1、ω2和相对隶属度η31、η32,按照式(13)求出可变模型参数α和β的4种组合所对应的4个综合隶属度,结果见表1。计算平均值可得满足归一化要求的综合隶属度V=0.851。