面向新型电力系统的储能规划与运行控制技术
2024-05-22国网长春供电公司黄峻航
国网长春供电公司 黄峻航
1 新型电力系统储能所面临的问题
在全面促进碳中和以及碳达峰的发展背景之下,促使电力能源应用领域受到一定影响,在传统电力供需视角下,不断提高新能源渗透率的过程中促使电力系统的储能表现面临严峻挑战[1],尤其是在2022年经由国家发改委以及国家能源局联合推出十四五新型储能发展方案后,为电力系统中的用户、电网以及电源等提出了多元化的储能应用意见。包括太阳能以及风能在内的各种清洁能源其不稳定性、分散性以及波动性等相对较强,因此探索合理的储能方案并对其加以控制成为促进电网平稳运行的关键所在。电力系统储能包括电力供需、电源及需求侧的管理等,考虑到储能系统的基础功能,对其展开合理的设计规划至关重要,将直接影响新型电力系统是否能够满足当前用电需求。
2 面向新型电力系统的储能规划
早期电力系统均以集中储能电站为主,这样的储能系统规模相对较大且成本较高,在运行使用过程中需消耗大量人力物力加以维护,均集中在电力公司以及政府部门的规划之外。而本公司所提出的分布式储能系统建设成本更加低廉且占地面积小,具有更加鲜明的应用优势。与此同时,分布式储能系统经常用于电力能源的负荷应急以及就地储存等,不受电网控制,导致难以对电网调控起到直接参与作用,进而影响其使用价值。为了更好的满足当前全新电力系统引用下的灵活配电网使用需求,本公司基于现有分布式储能系统,结合环节电压偏差、负荷管理以及削峰填谷等提出了一定的优化建议,进而设计出一种全新的储能规划模型,目的是减小电力系统运行过程中的储能网络损耗,进而满足负荷管理要求。
3 分布式储能规划与运行控制实践
针对以往新型电力系统应用过程中的储能系统出现电压越限及网络损耗等问题,影响配电网的运行效率,本公司提出一种全新的假设,通过创建线性最优潮流模型的方式,对以往配电网中R/X 建模准确度不足的问题加以解决,通过分析配电网的潮流特性,以储能规划最小成本为目标出发,提出分布式储能系统的规划模型,并根据配电网的不同运行节点,设计基于双有源桥下的钳位变换器结构控制方案,并验证该方案是否能够满足电力系统的运行应用效果。
3.1 场景设定
基于分布式储能规划在电力系统中的分布方式,本质上是通过区域到节点,对其中所有的不确定因素以及初步规划问题等加以考虑。首先应当创建配电网节点边际电价模型(DLMP),随后对电力系统配电网运行过程中最为薄弱的区域加以定位,作为接引分布式储能系统的后选位置,并利用价格信号对全新的电力资源合理配置[2]。
3.2 分布式储能规划
与传统电力设备对电压越限加以限制的行为不同,对电力资源加以应用并管理配电网是最为有效的手段。而DLMP 概念在电力系统的储能规划中加以运用,是考虑到成本价格信号的存在,以此为指标规划分布式储能,则能够对新型电力系统中可再生能源逐步渗透导致的电压越限问题加以控制。因此对分布式储能规划中的初步描述可界定为不大确定的DLMP 边界波动问题。根据信息薄弱区域对分布式储能加以接引,以期对其电能质量起到改善作用。因此在本方案设计中,通过与典型最优潮流方法相结合,提出了电网经济调度的解法,获得了基于对分布式储能初步规划的DLMP 公式:
式中:λp、μi是相应约束的拉格朗日乘子;p(z)表示等式约束;gi表示不等式约束;F(z)表示为储能总量;L(z)为成本控制目标。根据KKT 条件,则对于DLMP 展开的详细定义如公式(5)所示,通过该公式可对分布式储能规划的科学性、经济性等加以验证。需注意,在本方案设计中假设电力系统中的用户可自主调整无功功率,因此在DLMP 中不考虑无功功率的存在[3]。则构成了:
式中:λp表示为等式约束条件下的影子价格;Ptloss为t时刻下的有功损耗;load表示为额定损耗上限;res表示为配电网当前受电功率;LCC表示为损耗成本分量;ECC表示为能量成本分量;B、N分别表示为发电机影子价格与发电机总数;i表示为发电机;t为时刻;j表示i发电机的对应节点。
通过DLMP 下的储能成本估算模型,对电力系统储能运行过程中出现的超电压限制以及超高网络损耗等用电成本问题加以分析研究。基于实际角度来讲,通常情况下DLMP 在配电网中的价格区间处于较为合理的范围,而在公式(5)中则可以对配电网中的价格薄弱区域加以精准界定,在配电网中的DLMP 超出合理价格范围时,就相应的衍生出了薄弱区域。事实上,可再生资源以及电力负荷等均会影响配电网价格成本的薄弱区域,并且在不断增加调节参数的过程中,配电网的储能调度也将会呈现出一定的恶劣情况,即表示为不确定参数对最坏情况加以限制。
因此,若具有越高的不确定调节参数,则会导致DLMP 出现剧烈的波动现象,薄弱区域更加突出,有利于对其加以划定,证明通过分布式储能规划能够充分满足配电网的运行需求。在对配电网最薄弱区域加以分析的过程中设计了三种方案,根据DLMP>α 的原理可获得配电网薄弱区域,则在本次设计中,方案一设计为DLMP>α=45元/MWh 下配电网中的所有薄弱区域集合;方案二设计为DLMP>α=$50/MWh 下配电网中的所有薄弱区域集合;而方案三则设计为当DLMP>α=45元/MWh 时所对应的经典薄弱区域,即表示为方案三中的薄弱区域属于前两者中的一个子集[4]。
3.3 调节模型保守度
基于上文研究,在有关电力系统运行保守性方面可通过Γ 对鲁棒性加以优化,选择整数为基准,则根据上文中的三种设计方案,选择方案一的规划内容对不确定调节参数的保守度加以调节,设置Γ分别为0、6以及12。其中等于0的状态则是表示输出功率与标称值之间在任何时刻下均保持相一致的参数可界定确定性,而在不断增大参数的过程中表示新型电力系统中的可再生电能不确定度增加,并提高电力系统负载,表示标称值以及输出功率出现偏差的时刻相应增多。
由于不确定调节参数提高,则在电力系统中的分布式系统将会对冗余的可再生电力能源加以调节,促使其提升资源分配利用效率,进而在电力市场利润上行的阶段将冗余资源分拨为上层电网加以交易,促使自身的运行成本有效降低。表1为在差异性不确定参数下的分布式储能规划对比。
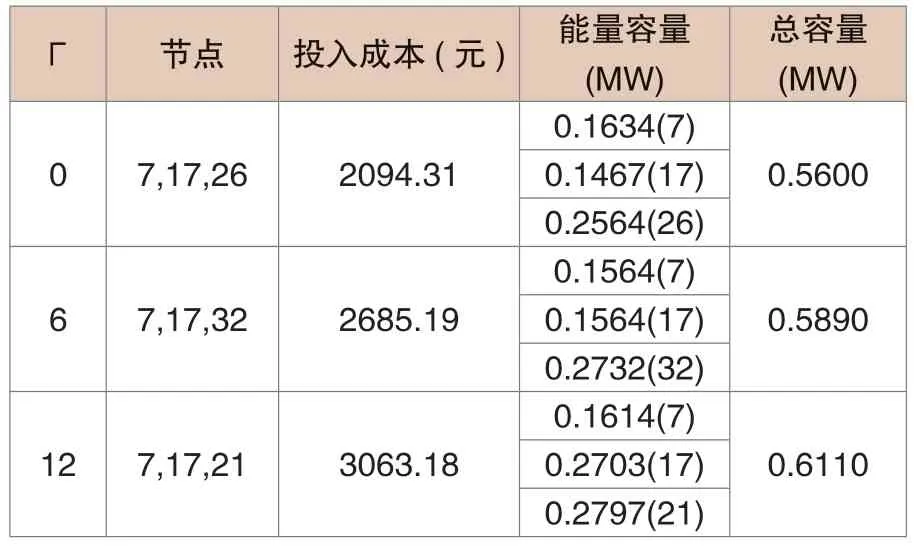
表1 分布式储能规划影响结果
根据表1中数据可得,在进一步增加Γ 的过程中分布式储能规划系统具有更加良好的处理能力,解决电力系统运行过程中的不确定性,进而促使投入成本相应增加。在相关研究中表明,在鲁棒优化的决策中纳入了最坏情况,进而促使分布式储能规划具有更加良好的鲁棒性。因此若电网具有越高的不确定调节参数,将会导致经济性受到影响,进而增强了风险应对能力,即表示具有更高保守度[5]。
3.4 鲁棒性与ARO 对比
根据文中内容对比了传统ARO 以及鲁棒性优化的随机结果,如表2所示。经过DLMP 模型可直观的了解到通过鲁棒性边界加以描述,发现相较于传统ARO 来讲,在鲁棒性优化下的分布式储能规划随机场景中的投入成本均低于前者,促使不确定性得以解决。
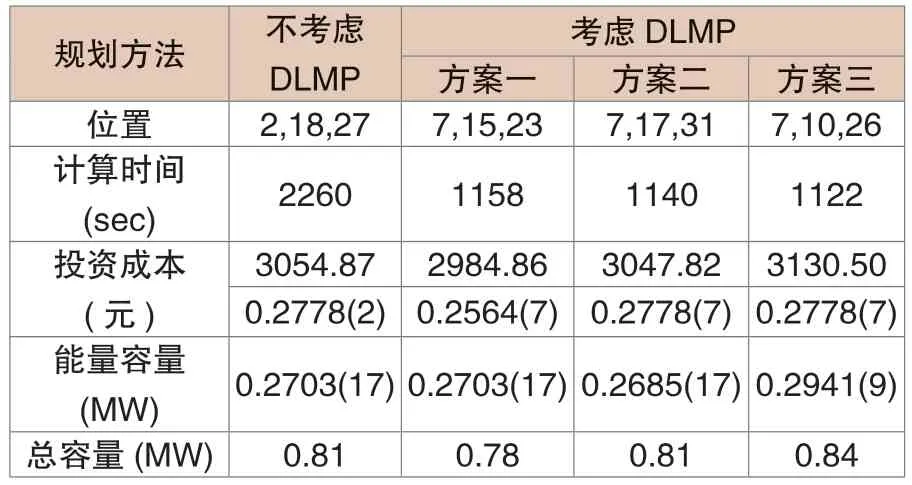
表2 鲁棒性与ARO 对比结果
3.5 双有源桥钳位变换器控制
经对本文所设计的方案选择分布式储能规划在电力系统中加以运行,能够对不确定参数加以调节,进而获得更加稳定的运行条件,降低成本并有效提升资源利用率,证明分布式储能规划有效。而在此基础上需要对其展开合理的运行控制,促使其充分发挥有效价值。钳位控制器的原理则是通过给定开关S0的运行周期以及占空比,基于d=TON/TO(式中:d表示为运行周期;TO表示为运行周期;TON为占空比)的定义,则可对开关S0定义为:λ1=1-d,式中:d表示为运行周期;λ1表示为非运行周期。同时也可通过开关运行周期TO与变换器运行周期Ts确定开关周期比:λ2=TO/Ts,式中:开关运行周期TO;变换器运行周期Ts。
基于此,则在变换器开关周期比以及钳位开关占空比的作用下对变换器的PWN 移相加以控制,对有源桥的工作过程加以控制,形成更高自由度,进而以传输功率表作为控制量,满足动态化的高度自由控制效果,促使分布式储能系统在前卫变换器的作用下具有更加灵活的功率调节效果[6]。
综上所述,在满足双碳发展的基础上,新型电力系统也面临着一定的困扰,储能系统是决定各种新型清洁能源稳定运行的关键,因此应当重点做好规划与运行控制。
