例说图形的平移
2024-05-22陈琼
陈琼

抓住图形平移的特点,掌握图 形平移的规律,有利于同学们提高 解题能力.
人教版数学教科书七年级下册第31页第6题的内容为:
如图1,在一块长为am,宽为bm的长方形草地上有一条弯曲的小路,小路的左边 线向右平移1m就是它的右边线.求这块草 地的绿地面积.
解决此题较简单,将图1中小路右边 的图形向左平移1m,则图1中的小路左右 边线重合,如图2.比较图1和图2,可以发现 它们长相差1m,宽均为bm,于是得到这块 草地的绿地面积为(a-1)bm?.
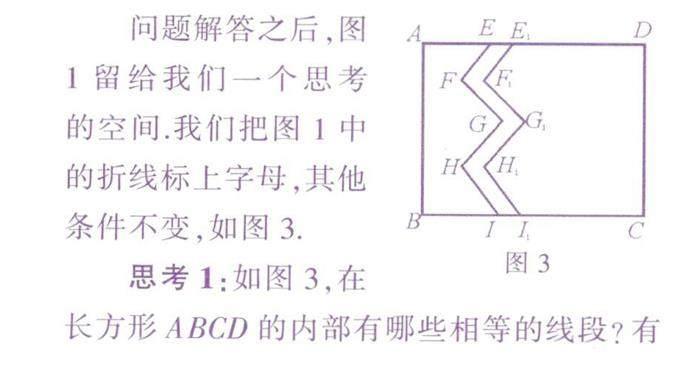
问题解答之后,图 1留给我们一个思考 的空间.我们把图1中 的折线标上字母,其他 条件不变,如图3.
思考1:如图3,在长方形ABCD的内部有哪些相等的线段?有哪些相等的角?
分析:根据平移的性质,容易得到EF=EF1,FG=F1G1,GH=G1H1,HI = HI1LF= ∠F1,∠G=∠G1,∠H=∠H1。
思考2:如果连接FF1,GG1,HH1,那么FF1,GG1,HH1之间有何数量、位置关系?
分析:点F与F1,点G与G1,点H与H1 分别是平移过程中的对应点,根据平移的性质, 容易得到FF1=GG1=HH1,并且FF1//GG1//HH1.
思考3:如图4,∠AEF,莱弗格,∠FGH,∠GHI,∠HIB之间有何数量关系?
分析:分别过点F,g,H作FP//AE,GQAE、HW//AE、而AE//BI,根据平行线的性质,得到:AE//FP/GQ//HW//BI.所以AEF=LEFP, LFGQ= ∠ PFG, ∠QGH= ∠GHW,∠HIB=∠IHW.以上四式相加,得到:∠AEF + ∠FGQ+ ∠QGH + ∠HIB= ∠EFP+∠PFG+∠GHW+∠IHW.故∠AEF+∠FGH+∠HIB= ∠EFG+ ∠GHI.
需要说明的是,可以将图4 简化为一个基本模型,如图5, 类似得出一个有用的结论:如 图5,如果AB//CD,那么人∠ABE+∠CDE=∠BED。
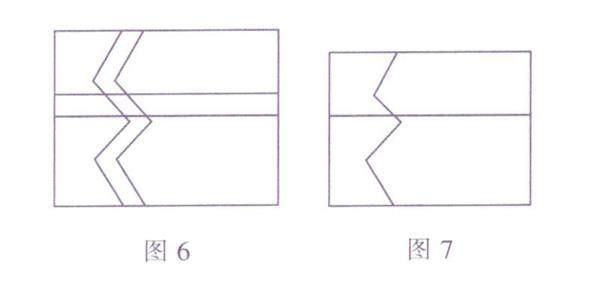
变式1:在一块长为am,宽为bm的长方形草地上有一条弯曲的小路,小路的左边 线向右平移1m就是它的右边线,再修建一 条平行于长边,且宽为1m的小路,如图6, 你能求出这块草地的绿地面积吗?
分析:能.先将图6中弯曲小路右边的 图形向左平移1m,则小路的左右边线重合, 再将水平小路上方的图形向下平移1m,最 后得到一个长为(a-1)m,宽为(b-1)m的长 方形,如图7.可得到这块草地的绿地面积为(a-1)(b-1)m2.
思考:变式1中,水平小路的边线与长 方形的长边平行,如果水平小路的边线与长 方形的长边不平行,路口宽为1m,如图8, 还能用上面的方法得出相同的结果吗?
分析:如果水平小路的边线与长方形 的长边不平行,则弯曲小路与水平小路重叠 部分的面积不一定是1m?,故不能用上面的 方法得出相同的结果.借助于几何画板,按 照上面的平移方式,会发现在本图中的绿地 面积小于(a-1)(b-1)m2.
上述质疑释惑的过程给我们一个启示: 用整体思想方法解题时,对于条件或图形结 构类似,但本质有所不同的问题,要仔细分 析,切记不要用原有的经验想当然地生搬硬套,谨防出错.
变式2:在长为am,宽为bm的长方形 草地上,有一些小路,小路的边线与长方形的 边平行或垂直,小路路口宽为1m,如图9.你能求出这块草地的绿地面积吗?
分析:先将图中小路右边的图形向左 平移1m,再将小路上方的图形向下平移 1m,得到一个长为(a-1)m,宽为(b-1)m的 长方形.于是得到这块草地的绿地面积为(a-1)(B- 1)m2。
思考:变式2中,如果小路的边线与长 方形的边不平行或不垂直,小路路口宽仍为 1m,如图10,还能用上面的方法得出相同的 结果吗?
分析:如果小路的邊线与长方形的边 不平行或不垂直,则图中的不同方向的小路 重叠部分有两块,其面积均不一定是1m?, 故不能用上面的方法得出相同的结果.借助 于几何画板,按照上面的平移方式,会发现 本图中的绿地面积大于(a-1)(b-1)m?.
总之,解决图形平移中的计算问题时, 一定要把握图形平移过程中相关线段、角以 及面积的不变性规律,并且要善于区分相似 图形结构中的不同特征,以达到正确解决问 题的目的.
