多角度探究圆锥曲线中的定值问题——以2023年高考数学全国乙卷理科第20题为例

⦿ 浙江省湖州市滨湖高级中学 郑梦华

⦿ 浙江省湖州中学 祝峰泽

1 真题再现

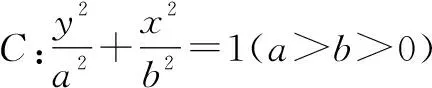
(1)求C的方程;

(2)过点(-2,3)的直线交C于P,Q两点,直线AP,AQ与y轴的交点分别为M,N,证明：线段MN的中点为定点．

分析：第(1)问求椭圆的标准方程,属较易题;第(2)问解析可采用常规的韦达定理方法,本文中不再赘述.本题第(2)问考查学生运用坐标解决平面解析几何问题的能力,较好地考查学生的数学运算素养.

2 追本溯源

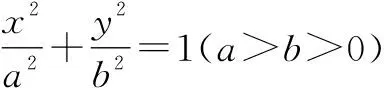
(1)求E的方程;

(2)证明：直线CD过定点.

该题是一道常规的解析几何题,命制背景为极点和极线,考查了解析几何的基本思想和基本方法,对学生的运算能力要求很高,很好地起到了区分的作用.该类型题目在近年高考卷中也多次出现,例如,2010年的江苏卷第18题.因此,研究高考真题是教师最重要的教学策略之一.

3 真题第(2)问的解法赏析

解法一：平移坐标系角度.

评注：对于第(2)问,如果利用常规方法求解,因为直线PQ经过的点不在坐标轴上,所以联立方程后的计算量非常大,而使用解法一能够极大减小计算量,但难点在于坐标系平移前后的各点坐标变化,对学生的数形结合思想要求较高.

解法二：参数方程角度.

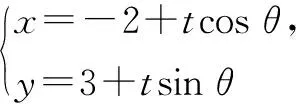
评注：解法二从直线PQ的倾斜角入手,利用直线的参数方程解决问题.在运算的过程中还需用到三角恒等变换的一些知识,计算量小,非常简洁.

解法三：定比点差法角度.

①

评注：定比点差法,其本质是利用定比分点和圆锥曲线方程中横、纵坐标表达式的一致性,优化运算过程的变形手段,是处理圆锥曲线弦上三点问题的一大通法.

解法四：构造二次方程角度.

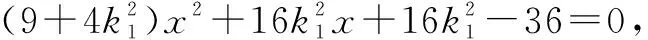
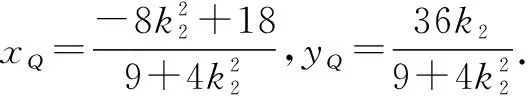
设直线PQ方程为y=k(x+2)+3,将点P,Q的坐标分别代入直线方程,可得

即k1,k2是方程12x2-36x+36k+27=0的两个根,易知yM+yN=2(k1+k2)=6,即证得直线MN的中点为定点(0,3).

评注：解法四着重考查函数与方程的思想,尤其是函数问题中常用的同构思想,技巧性较强,同时大大减小了运算量,在解题过程中起到了事半功倍的效果.

解法五：二次曲线系方程角度.

引理：过平面上三点A,B,D及点A的切线l的二次曲线系方程可设为l·lBD+λlAB·lAD=0.

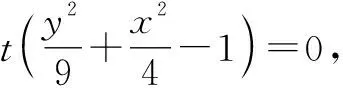
评注：解法五应用二次曲线系方程[2]中过三点及一条切线的二次曲线方程,随后利用待定系数法将所设方程和原椭圆方程进行对比从而求出参数,该解法非高中数学常规内容,多用于竞赛题的求解.

前文提到过该题的背景是极点极线,在高中的视角下,极点极线经常用于命制圆锥曲线的切线和切点弦模型试题.笔者不禁思考：在一般的椭圆方程中是否还有类似规律呢?如果点D为直线x=-a上任意一点,过点D作椭圆的两条切线,得到的切点弦即为极线,此时是否还有类似结论?对于双曲线和抛物线呢?

4 推广探究

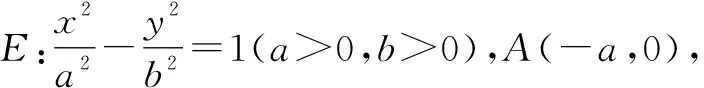
推广4(纵向推广)已知抛物线方程：y2=2px(p>0),A为坐标原点,过y轴上任一点D(非点A)作抛物线的两条切线切于点A,B,过点D作一条直线交抛物线于P,Q两点,设直线AB,AP,AQ的斜率分别为k0,k1,k2,则k1+k2=2k0.

5 结束语

通过上述多角度探究、思考与推广探究,真题本质也逐渐被揭开,同时,也启示我们在日常教学中要抓住问题的本质.教师在教学中可以适当补充一些一类问题的本源,尤其是经常作为高考真题的命制背景问题;学生也可以适当总结问题的本质,从而提高核心素养,提高数学解题能力.