“生本”理念下精彩习题课堂的建构

⦿ 江苏省常熟中学 陈婷婷

习题课是数学教学的重要课型,它既可以检测学生知识、技能、方法的掌握情况,也可以帮助学生查缺补漏、开阔思路、积累经验、建构知识体系[1].习题课用不着面面俱到,如果每道题都讲、每个知识点都强调,那么习题课就上成了新授课,这样所讲知识过于繁杂,不仅影响个体知识结构的建立与完善,而且容易造成学生思维疲劳,难以发挥习题课的育人价值,影响习题课的教学质量.在习题课教学中,教师要重视归类、总结,重视呈现学生的思考过程,引导学生探寻问题的本质,以此达到会一题、通一类的效果,切实提高习题课教学的有效性.笔者以“椭圆习题课”教学为例,谈谈对习题课教学的几点浅见,若有不足,请指正!

1 教学简录

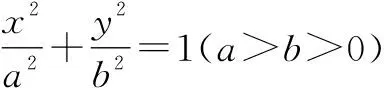
该题解法不唯一,教师鼓励学生尝试应用不同的方法解决问题.问题给出后,教师预留充足的时间让学生思考,然后充分展示学生的思考过程.

师：谁来说一说,你想利用什么方法解决这一问题呢?

生1：设点P的坐标为(x,y),通过消元将问题转化为主元是x的二次函数,在定义域[-a,a]上求最值.

生2：我和生1的想法基本相同,不过我通过消元将问题转化为主元是y的二次函数,在定义域[-b,b]上求最值.

师：还有其他解决方案吗?

生3：还可以设P(acosA,bsinA),这样可以将问题转化为主元为cosA或sinA的二次函数,在定义域[-1,1]上求最值.

师：非常好,以上同学给出的方法是解决此类问题常用的方法,通过消元,将问题转化为二次函数,利用二次函数求最值的经验解决问题.

教师正准备让学生任选一种方法,完善解题过程时,生4又给出了另一种解法.

生4：以上都是从数的角度分析,其实该题还可以从形的角度分析,将目标看成圆与椭圆相切的两个状态就是最值.(部分学生投来疑惑的眼神.)

师：是个不错的想法,请具体说说你的想法.

生4在黑板上画出了两个临界状态,学生恍然大悟.

师：你认为哪种方法是最优解法呢?

通过互动交流,最终达成共识：若该题是填空题,可以选择生4的方法来解决,借助几何直观,可以优化运算过程,提高解题效率;若该题是解答题,则需要利用前面几位同学给出的代数法进行推理.

教学评注：教学中,教师将课堂还给学生,鼓励学生应用不同方法解决问题,有利于激活思维,激发潜能,这样学生的思维动起来了,课堂也就活起来了,有利于提升教学有效性[2].

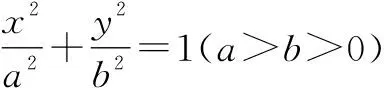
同样,问题给出后,教师没有急于呈现标准答案,而是将解题主动权交给学生.学生独立求解,教师巡视.从解题反馈来看,学生给出了不同的答案：4个;4个或2个或0个;4个或0个.基于此,教师给出如下解题过程：

教师话音刚落,学生提出异议.

师：真的吗?

生6：两个解时,显然与题目中“异于顶点”相矛盾,应舍去.

此时,给出两个解的学生恍然大悟.

这样通过师生互动交流,最终明确,点P有4个或0个.

师：现在我们将题目变一变,若将“∠F1PF2=60°”改为“∠F1PF2=90°”,你有什么发现?

改编后,学生联想到圆.在此基础上,教师又引导学生将椭圆向特殊化转化,让学生体会离心率变化带来的视觉冲击.当然,也有学生提出将角向一般化转化,如令∠F1PF2=θ.这样通过特殊与一般转化,既有利于发散学生的数学思维,拓宽学生的视野,又利于增强学生的解题信心.

教学评注：教学中教师要充分发挥课堂主导的作用,当学生出现分歧或困惑时及时给予引导,以此增强学生学习信心.此环节,教师引导学生将问题进行改编,以此通过变式使习题变得更有广度、更有深意,有利于揭示问题的本质,提升学生数学素养.

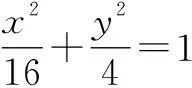
中点弦问题是高考的一个重要考点,教师让学生以小组为单位,共同探索解题思路.

生8：可以利用方程组法求解,设斜率,联立方程,利用设而不求的方法解题.解题时需要注意,设斜率需要考虑斜率是否存在,该题根据已知条件可知,直线AB的斜率是存在的,所以设所求的方程为y-1=k(x-2)即可.

师：很好,方程组法是解决椭圆中点弦问题的常用方法,将直线方程与椭圆组成的方程组,通过消元将其转化为一元二次方程,从而利用一元二次方程根与系数的关系及中点坐标公式可以求出斜率,以此得到直线方程.还有其他方法吗?

生9：设点A(x,y),则由对称性得B(4-x,2-y),利用这两点都在椭圆上,即可得到所求.

师：非常好,利用对称性解决了问题.该方法就是我们常说的中点转移法.解题时,先设弦的一个端点坐标,然后借助中点坐标,可以得到另一端点坐标,将两点分别代入椭圆方程,直接相减即可得到所求的直线方程.

生10：也可以分别设出A,B两点坐标,然后将两点坐标分别代入椭圆方程,两式相减可以求得直线斜率.这样得到直线斜率后,问题即可迎刃而解.

师：非常棒,该方法可以称其为“点差法”,是解决中点弦问题的一个不错方法.

生11：其实这个题单凭看也能得到答案.

师：哦!你是怎么看的呢?

生11：直接写出上顶点和右顶点的坐标,它们的中点就是点M,这样可以直接写出直线方程.

学生纷纷投来羡慕的目光.

师：太厉害了,凭借直观思考,一眼看穿!若将点M坐标改为(1,2)呢?

这样更改后,显然利用生11的方法行不通了,由此通过对比既让学生感知通法的通用性,也让学生体会几何直观的优越性.

教学评注：在此过程中,生11利用直觉思维,借助几何直观高效地解决了问题,充分展示了数形结合的魅力,不过该解法具有一定的特殊性.在日常教学中,我们不仅要强调通法,也要关注最优解法,对于一些客观题,若能用优法解题,可以达到事半功倍的效果.对于该题,教师还可以引导学生想一想,若点M不是弦的中点该如何求解,由此让学生体会方程组法才是解析几何最重要的解法.

2 教学思考

习题课上,教师切勿“求多”,而是要“求精”.教学中,教师要认真研究“课标”和真题,结合教学经验和学生学习反馈精心挑选典型性例题,以此充分发挥典型例题的辐射功能,提高学生举一反三的能力[3].

习题课上,教师切勿大包大揽,应该将课堂还给学生,学会倾听学生的想法,关注他们的思考过程,鼓励他们合作交流,充分发挥学生的主体价值,让不同思维碰撞出火花,以此拓宽学生的视野,激活学生的思维,促成深度学习.

值得注意的是,我们强调学生的主体价值,切忌忽视教师的主导作用,教师作为课堂教学的组织者、引领者,其在教学中的地位和作用是不可替代的.在课堂教学中,教师既要做好充分的预设,又要及时捕捉各种课堂生成.当课堂上出现“意外”时,要根据实际情况及时调整教学节奏和教学策略.如当学生困惑时,教师要适当地放慢脚步,通过多角度分析帮助学生排疑解惑,以此让学生真懂真会;当学生提供精彩的解法时,教师要给予充分肯定,激发学生学习兴趣,升华学生认知.

总之,若想打造精彩的习题课堂,教师就要放权给学生,让学生主动交流各自的所思、所想、所惑,让学生把题真正地学懂、吃透,切实提高学生解题能力.同时,在课堂教学中,教师要及时引导学生总结和反思,以此优化个体认知结构,提高学生举一反三的能力.