基于数值模型的气动噪声预测计算方法研究

郑超ZHENG Chao；王贺远WANG He-yuan；高启GAO Qi；崔永龙CUI Yong-long；谢志豪XIE Zhi-hao；李奇LI Qi；王帅皓WANG Shuai-hao

（中国船舶及海洋工程设计研究院，上海 200011）

1 气动噪声理论研究的发展

随着当今社会工业化进程的飞速发展，气动噪声问题已逐渐成为工业发展中的重要议题。例如，在航空工业领域，欧美一些发达国家已将航空噪声指标作为适航的关键指标，并针对航空气动噪声问题制定了长期的战略目标和详细的降噪规划。在我国，机场噪声控制方面也制定了相关规范，对飞机起降噪声提出了明确要求[1]。

历史上，气动声学的早期研究主要集中于涡喷发动机产生的射流噪声问题，这一问题也是该领域的起源和研究的具体起点。早期人们（甚至现在一些接受非流体背景训练的工程师和研究人员）认为射流噪声问题是流体射流冲击发动机喷管引起的喷管振动发声，并试图通过将射流噪声问题转化为经典声学中的板、壁、壳振动发声问题进行求解。然而，1952 年Lilley 进行了一个简单实验，通过改变流场中的扰动来改变噪声模态，从而否定了这种看法[2]。同年，Lighthill[3]提出了以自己名字命名的处理喷射噪声问题的声类比理论方程——Lighthill 方程，它建立了声压波动量与流场物理量之间的关联，该方程是研究气动声学的奠基之作，对、气动噪声场分析、气动噪声研究预测、气动噪声装置设计等有着重要的指导作用。

Lighthill 博士是近代气动声学理论的先驱之一，他在气动噪声学上的影响极为深远。他的理论为自由空间内的喷气噪声等问题的研究，提供了重要的基础，对于没有固体边界的噪声场，该方程依然适用。他的理论对流体动力噪声的研究和设计产生了深远的影响。1955 年，Curle[4]在Lighthill 的基础上，考虑了静止固体壁面对气流发声的影响，使用基尔霍夫方法对Lighthill 方程进行了改进，推导出了Curle 方程。1969 年，Ffowcs-Williams 和Hawkings[5]在Curle 的理论基础上应用广义函数法，将Curle 的结果进行推广，考虑了运动固体边界对噪声的影响，得到了一个较为普适的方程称为FW-H 方程。

除了Lighthill 方程，自19 世纪60 年代以来，Powell[6]、Doak[7-8]、Howe[9]等学者基于流体噪声的产生机制、声波与湍流之间的相互作用等问题进行深入研究，提出了涡声理论。涡声理论是在Lighthill 方程之后，一种重要的气动噪声计算理论。它考虑了声波与湍流之间的相互作用，通过联合求解流体动力学和声学方程，来预测气动噪声的特性。尽管与Lighthill 的理论相比，它在实际气动噪声预测中的应用效果并不理想。然而，它在理论层面上仍然具有重要的价值，有助于解释一些关键的实验现象。因此，涡声理论在气动声学的复杂研究中扮演了重要的角色，推动了该领域的发展。

2 气动噪声预测的数值计算方法

如今对气动噪声的预测主要是建立在CFD 计算的基础之上[10-13]，即根据流场计算的结果作为声源输入至气动噪声计算，并结合声类比法对噪声结果进行预测，这是一种非常有效的研究方法。通过将流场计算结果与声类比法的结合，可以更准确地预测气动噪声的性质和分布。这种方法可以帮助研究者更好地理解气动噪声的产生机制，为设计和优化空气动力噪声相关的设备或系统提供重要的参考。（如图1 所示）。目前，气动噪声的数值计算方法有以下三种：计算气动声学方法（Computational Aero-Acoustic，简称CAA）、莱特希尔声类比方法（Lighthill's Acoustic Analogy）以及混合计算方法（Hybrid Method）。

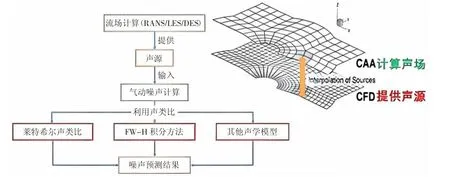
图1 气动噪声数值计算方法

当对某个气动噪声场进行预测时，需要根据具体情况进行选择恰当的数值计算方法，以确保结果的准确性和有用性。如果处理模型小且需要深入了解气动噪声内部产生机理的问题时，可以考虑采用计算气动声学方法（CAA），这种方法具有高精度，但计算量大的特点。当处理工程中常见的单一气动噪声问题，可以使用CFD 软件中的莱特希尔声类比方法进行计算。这种方法在预测远场噪声时精度较高，但在近场噪声方面可能会因模型大小、流场变化、结构振动等因素引起误差。因此，在应用此方法时，需要综合考虑计算需求或预测期望，进行调整优化。

当考虑结构共振效应、材料吸声特性等影响因子时，需要采用更为多元的混合计算方法。这种方法能够更真实地预测工程中的气动噪声，全面考虑各种因素对气动噪声的影响。这种方法不仅适用于计算远场噪声，还能精确预测近场噪声的分布和特性。当然此方法也需要更多调用更多的计算资源。总之，选择合适的方法需要根据具体的研究需求和计算条件进行计算模型的编写和调整，以确保能够得到准确且有用的结果预测。

ANSYS Fluent 中自带的有四种噪声算法，分别为FW-H 声学比拟法、宽频噪声模型、CAA 直接模拟计算以及流体软件与声学软件联合仿真[14]。

通过计算气动声学方法（CAA）求解流体动力学方程，可以更真实地预测工程中的气动噪声，揭示实际问题中声波的产生与传播。为了确保声波预测的准确性，该方法依赖于控制方程在时间上的精确解。这些条件导致了较高的计算成本。

当处理远场噪声问题时（比如噪声在数百倍机翼弦进行长远距离传播），计算气动声学方法需要大规模的并行计算支持，需要投入大量的计算资源。在处理近场噪声问题时（如机身上的APU 噪声、空穴噪声以及由微小部件引起的扰动噪声），计算气动声学方法在小模型方面则更具优势。

另外，气动噪声预测结果的准确性还依赖于流场计算结果的准确性，且声学软件对网格有特殊的要求，即网格中最大单元的边长应小于计算频率的最短波长的六分之一[11]。因为较小的网格尺寸能够更好地捕捉到声波的传播和反射特性。对于高频计算，由于波长非常短，导致网格数量急剧增加，因此需要更加精细的网格来准确模拟这些高频噪声。

针对本项目的实例，下面主要介绍FW-H 噪声模型以及宽频噪声模型。

2.1 FW-H 声学比拟法

目前已有很多商用CFD 软件中包含莱特希尔声学比拟模型[15]，用于流场和声场的耦合仿真。一般来说，首先需要对流场进行计算，然后使用声学比拟理论将流场数据转化为声源，最后计算声场辐射[16-17]。

FW-H 声学比拟法是一种广泛应用于解决工程问题的声学模拟方法，它具有以下优点：

①计算量较小：与CAA 算法相比，FW-H 声学比拟法对网格的要求较低，计算量和计算格式的要求也相对较低，更适合于解决工程问题。

②分离计算声音的产生和声波的传播：FW-H 声学比拟法将声音的产生和声波的传播分开计算，将流场仿真结果作为边界条件代入声场，使声场计算相对孤立，仅考虑流场对声场的作用效果。

预测气动噪声的FW-H 声学比拟法建立在获得近场流动解的基础上，通过运用积分法由近到远，求得远场观测点处的气动噪声。该方法将近场流动解作为声源信号，并在非稳态流场中用一系列分布式的等效声源分布来代替这些非均匀性对声音传播的影响[18]。这种方法能够更全面地考虑各种因素，如流场的细节、流速的变化、压力分布的不均匀性等，对气动噪声的影响。为了更精确地模拟这些影响，声学比拟法采用了分布式声源的策略。它能够模拟一系列等效声源在空间中的分布，以更好地反映流场的非均匀性对声音传播的复杂影响[19]。这种方法克服了传统预测方法的局限性，能够更全面、更深入地考虑各种因素对气动噪声的影响，从而提供更准确、更可靠的预测结果。

在深入剖析流体近场流动的过程中，选取恰当的控制方程至关重要。诸如非定常雷诺平均、DNS（直接数值模拟）以及LES（大涡模拟）等方法，均被用作求解流动特性的有效手段。我们将这些求解结果视为噪声源，进而通过波动方程的求解获得精确的解析解。这种方法巧妙地将流动求解过程与声学分析相分离，使得两者能够独立而精确地进行。

同样，FW-H 声场计算的结果在很大程度上依赖于流场计算的准确性。因此，流场湍流模型的选择变得尤为关键。在Fluent 噪声模型中，我们拥有四种主要的湍流模型：直接模拟模型（Direct Simulation，DNS）、大涡模拟模型（Large Eddy Simulation，LES）以及雷诺时均方程法（Rein's Reynolds-Averaged Navier-Stokes，BANS）。其中，LES 方法因其独特的优势而备受青睐。与DNS 相比，LES 无需解析极小的涡流，而是采用近似模型，即亚网格尺度（SGS）应力模型，从而显著降低了计算成本。同时，与RANS 相比，亚格子应力模型展现出更广泛的适用性。因此，在利用FW-H 声学比拟法时，我们通常选择LES 作为湍流模型进行计算，以确保结果的准确性和效率[26]。

2.1.1 FW-H 方程

Lighthill 方程基于流体动力学N-S 方程[20]，其方程形式为：

基于Lighthill 提出的声学比拟方法，Ffowcs-Williams与Hawkings 通过引入Heaviside 函数H（f）及其导数Dirac函数δ（f）[5]，从而推导出了著名的FW-H 方程：

方程（2）右边的三项分别代表了不同的声源机制：第一项是单极子声源，源于容积移动效应；第二项是偶极子声源，由物体表面对流体的作用力所引起；而第三项则是四极子声源[21-22]，归因于流体的运动（如图2 所示）。例如，脉冲喷气会产生单极子声源噪声，物体表面的压力脉动会引发偶极子声源噪声，而喷流、尾迹和显著的分离流则会导致四极子声源噪声的产生[23]。

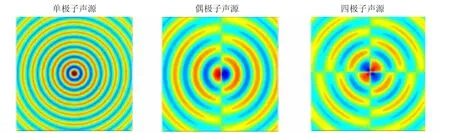
图2 气动声源的三种类型示意图

进一步的研究推导揭示了单极子、偶极子和四极子声源的总声功率与流速的密切关系：它们分别与流速的四次方、六次方和八次方成正比[24-25]。这一发现为我们深入理解气动声源提供了重要的理论依据。

通过求解非齐次的波动方程，可以获得FW-H 方程的积分解，进而描绘出远场噪声的分布图。在这个过程中，单极子则代表了远处传播的声波，它们对应于远场噪声的积分计算，能够准确描述远场噪声的分布图；偶极子代表了局部声源的影响，如物体表面的扰动或微小部件的振动，它们对应于面积分计算，能够精确描绘出近场噪声的分布。相比之下，四极子则代表了更大的范围和更复杂的声源分布，它们对应于体积分运算，能够在更大空间范围内考虑气动噪声的影响。这种方法可以帮助我们更好地理解和计算远场噪声。

另外，在计算远场噪声时，通过在积分面处引入广义函数，推导出基于波动方程的Kirchhoff 公式，用于远场噪声计算。该方法的推导过程是在假设声音传播完全遵循齐次波动方程（即不含有源项）的前提下进行的，因此该公式的应用具有一定局限性[26]。这一限制也提醒我们，在处理复杂的非线性声学问题时，寻找更加适用的理论工具和分析方法的重要性。

2.1.2 FW-H 噪声模型

FW-H 噪声比拟方法作为一种强大的工具，在工程领域得到了广泛应用，尤其在预测汽车和高速列车在高速行驶时产生的远场气动噪声方面表现出色[15]。在处理中场和远场噪声模拟时，ANSYS Fluent 软件采用了基于Lighthill的“噪声类比法”的声比拟模型（如图3 所示），在处理远场噪声距离远大于声波波长时的噪声情况时，将所有的气动声源都可以被视为由四极子、偶极子和单极子等基本声源的组合分布，不仅简化了计算，而且使噪声源的指向性估算更为简单，更易于得到噪声源的分布，并且Fluent 含有丰富且准确的流场仿真模型，可保证流场与声场耦合时边界条件输入的准确性。

图3 声比拟模型

声比拟模型的应用为噪声预测和控制提供了有力支持。但值得注意的是，目前的FW-H 噪声模型还不能预测封闭空间内或噪声向密闭空间内部的传播。

2.2 宽频噪声声源模型（Broadband）

在计算涉及湍流效应的流体噪声时，经常会遇到一种情况：噪声并不表现出明显的频率特征，这通常是因为湍流中的微小扰动和波动在各个频率下都产生噪声，使得噪声的频谱变得相对宽广，这种现象被称为宽频噪声。值得注意的是，ANSYS Fluent 中的宽频噪声模型不需要对湍流物理场进行瞬态求解。它主要通过稳态RANS 方程来获取流场的平均速度、湍流动能和湍流耗散率等关键参数，进行数值模拟，该方法使得计算更为简洁高效，且该模型除了能够计算出整个流场产生的总噪声能量外，还能提取噪声源的信息，帮助我们更好地了解进行噪声源分析及预测。

尽管宽频噪声模型的计算结果在精度上可能不如某些其他方法，但由于其基于稳态求解的特性，它的计算成本相对较低且耗时较少。因此，在对流体场壁面的噪声强度分布进行分析和预测时，宽频噪声源模型可以作为一种有效而实用的工具。

在ANSYS Fluent 中有如下半经验修正模型用于计算表面单元或体积单元的噪声功率。

2.2.1 Proudman 方程

Proudman 方程是Proudman 基于莱特希尔声学分析导出的由不含平均流动的各相同性湍流产生的声功率的计算公式，该方程适用的假设是：高雷诺数、低马赫数及各向同性湍流流动[27]。后来，Lilley 在Proudman 公式的基础上考虑了Proudman 公式中所忽略的迟滞时间对噪声计算的影响，这两个公式计算出的声功率都是基于单位体积的各向同性湍流计算得出的，单位体积流体内各向同性湍流产生的声功率为计算公式如下：

式中，α 为模型中的一个常数，u 和l 分别代表湍流速度和湍流长度尺度，a0为声速。

2.2.2 湍流边界层噪声源项（Turbulent Boundary Layer Noise）

基于声学类比，模拟、预测流体通过固体壁面时产生的宽频噪声，这种噪声的产生通常发生在较低的马赫数条件下，由边界层湍流引起。具体来说，可通过科尔积分公式根据流体的物理性质、边界条件以及声波传播特性进行计算，从而得出声功率等关键参数，其积分公式如下：

式中，τ为迟滞时间，τ=t-r/a0，S 为积分表面。

在ANSYS Fluent 中后处理变量中，Surface Acoustic Power[W/m2]或Surface Acoustic Power Level（dB）作为表面后处理积分量，具体公式如下：

Turbulent Boundary Layer Noise 源项模型在评估局部偶极子噪声源对总噪声能量的贡献方面非常有价值，对于流体动力噪声研究和设计来说是一种非常有用的工具。它能够模拟湍流边界层噪声的产生和传播，帮助我们更好地理解关键的噪声来源，并为降低流体动力噪声提供重要的指导。通过模拟装置周围的流场和噪声特性，我们可以快速评估装置对噪声场的影响，从而优化装置的设计。

2.2.3 线性欧拉方程的源项（Linearized Euler Equations）

线性化的欧拉方程（Linearized Euler Equations），简称LEE，是从纳维-斯托克斯方程（N-S Equations）中推导出的，它将方程中的流体变量转换为由时均值、湍流分量和噪声分量组成的形式。在进行线性化时，因噪声分量远小于时均值和湍流分量，所以忽略不计。当欧拉方程线性化后，产生的噪声分量可以写成以下形式：

上式中，含有下标a 的值为噪声分量，含有上标“′”的值为湍流分量。方程等号右边的前三式代表声源的主要成分，包含平均剪切流，代表剪切噪声源项；而第三式只含有湍流速度，被称为固有噪声项。这意味着在噪声产生中，剪切流和湍流速度是主要的声源成分，而噪声分量则是由这些成分的扰动所产生的。在进行流体动力噪声的研究和设计中，了解这些声源成分及其相互作用对于优化设计和降低噪声非常重要。由文献[28]可知，计算线性化欧拉方程所需的湍流速度场可以通过随机噪声产生和辐射的方法获得，速度场计算公式如式（9）所示：

2.2.4 Lilley 方程源项

Lilley 方程是一种三阶波动方程，它的本质仍为可压缩流体的质量守恒方程与动量守恒方程。当省略粘性条件后，其方程如式（10）所示：

式中，声源项可以通过随机噪声产生和辐射的方法获得平均速度流场，并由湍流速度成分计算得出。与线性化欧拉方程类似，声源项可以根据涉及速度梯度与否分为自噪声源项（Self-Noise）和剪切噪声源项（Shear-Noise）。自噪声源项与流体的平均速度梯度无关，而剪切噪声源项则与平均速度梯度有关，通常与流体的剪切力有关。这两种声源项在流体动力噪声的研究和设计中具有不同的作用和贡献。

3 总结

①声学比拟方法在气动噪声预测的数值计算中的特点在于它将声音的产生和声音的传播分开来计算，保证了流场与声场的独立性。与计算气动声学（CAA）方法相比，这种方法在计算量和计算格式要求上相对较低，使得其在实际应用中更为便捷。

然而，声类比方法也存在一定的局限性，它主要适用于远场噪声辐射的计算，而在近场噪声计算方面可能会产生较大的误差。尽管如此，由于其在工程应用中的价值，使得这种方法仍然具有重要的实际意义。

②宽频噪声模型作为CAA 和声学比拟方法的重要补充，这种模型不需要求解瞬态流动过程，而是基于雷诺时均方程的平均速度、湍流动能和湍流耗散率进行计算。通过量化每个单元表面或体的噪声贡献值，就能够计算出整个流场产生的噪声能量，大大减小了对计算资源的需求，提高了计算效率。并通过对噪声源的提取，查看噪声源的分布情况并分析出流场中的主要噪声源，从而迅速确定流动中哪一部分对噪声的影响最为显著，提高了噪声预测的准确性。