基于IQPSO-GA优化ANFIS模型的服务器故障预警方法

李盛新，叶丰华，李道童，张秀波，韩红瑞

(浪潮电子信息产业股份有限公司，济南 250101)

0 引言

随着我国计算机行业的空前发展，大数据、互联网+、云计算等新兴行业技术经过不断研究得到了广泛的应用。服务器随着这些信息技术的发展，在各领域得到了越来越广泛的应用，如军事、医疗、银行、互联网等领域[1-2]。若服务器底层硬件发生故障造成非预期的暂时停机，可能会导致数据丢失、应用中断等后果[3-4]。这就要求服务器具备高效率的故障诊断、检测和预警等技术的支持。因此，研究服务器硬件故障预警技术，建立底层业务类硬件故障预测模型，对提高服务器的可靠性、可用性具有重要的实用价值[5]。近年来，人工智能算法在各个科研工程领域的研究成果斐然，主要包括神经网络、仿生寻优算法、决策树、支持向量机等[6-9]，其高效的非线性数据拟合能力为服务器硬件故障预警提供了有效途径。尤其人工神经网络(ANNs，artificial neural networks)在工程应用和理论研究中都是非常热门的智能算法，被视为一个大规模、非线性化的数据融合处理系统，具有不受模型约束、学习能力强等优点。

文献[10]基于智能算法提出一种使用时间序列聚类检测服务器异常的方法，该方法虽然能够检测整个服务器系统是否异常，而无法定位检测服务器异常硬件，尤其是晶体管密度及规模小的器件。同时，时间序列聚类智能算法在可靠性方面存在一定劣势，不适用于服务器这种对可靠性要求极高的系统。ANNs作为一个多学科交叉的前沿技术，正向模拟人类认知的道路上更加深入发展，其与模糊系统、元启发式优化算法等结合对自身网络结构进行优化是一个重要研究方向[11]。自适应神经模糊推理系统(ANFIS，adaptive neuro fuzzy inference system)充分利用了ANNs和模糊推理系统(FIS，fuzzy inference system)二者的优良特性，与传统智能算法相比[12-13]，它的结构更复杂，计算能力更高，具有如下优点：1) 收敛速度更快；2)泛化能力更强；3)映射关系更稳定，即训练结果不随训练数据输入的顺序而改变。传统的ANFIS采用了梯度下降法对隶属度参数进行调整。这种方法在每一步梯度计算时都可能会出现局部最小值的问题，这会导致无法得到最优的模型输入和输出数据之间的映射关系，最终造成服务器硬件故障预警的误判和漏判问题的产生。

元启发式优化算法是随机算法与局部搜索算法相结合的产物[14-16]，通过采用一定的策略接收相对劣质解从而避免陷入局部最优。但现有的许多元启发式算法由于其自身的搜索策略设置，应用于实际搜索时存在相应的缺点，如蚁群优化算法计算量大耗时长、模拟退火算法收敛速度慢且需手动增加迭代次数等。粒子群优化(PSO，particle swarm optimization)由于其搜索速度快、建模简单的特性被广泛应用[17]，但其精度不高且在迭代后期粒子的速度受到一定限制不容易收敛[18]。2004年Sun等人[19]利用量子力学中的相关理论知识，提出了量子行为粒子群优化(QPSO，quantum-behavior particle swarm optimization)算法，参数设置比PSO算法少，在搜索能力上也更优。然而QPSO算法也无法突破粒子群迭代更新后期，种群粒子的多样性必然减少的限制[20]，最终导致其对搜索全局最优解的稳定性不强。文献[21]结合遗传算法(GA，genetic algorithm)与BP神经网络提出了云服务器请求量预测模型，实验证明具有不错的稳定性和准确性。GA在全局最优解的搜索上具有高效性，但该方法存在局部搜索能力弱，群体成熟早、效率低的问题，并不适用于单独搜索ANFIS隶属度参数。

基于上述分析，为获得更精确、更高效服务器预警模型[22]，本文提出一种改进的QPSO(IQPSO，improved QPSO)算法，并借鉴GA中的交叉变异思路设计一种新的混合元启发算法IQPSO-GA对ANFIS参数进行搜索，构造IQPSO-GA-ANFIS模型结构，以获得更优的模型预测能力，进而实现服务器故障预警功能。本文其余部分组织如下：第1节介绍了ANFIS结构及参数训练过程；第2节提出了IQPSO算法，并描述了IQPSO-GA混合元启发式优化算法的实现步骤；第3节给出了基于IQPSO-GA调整ANFIS参数的流程方法；第4节通过实验数据验证了所提方法建立预警模型的优越性；在第5节给出了本文的结论。

1 故障预警模型的建立

1.1 设置模型参数

当前业界应用的服务器硬件检测和预警技术主要有指标监控、日志分析、人工巡检、预测模型4种方法，其中前3种方法只是检测服务器的可观测指标参数，不具备实质上的预警意义。预测模型方法是通过历史数据建立预测模型，由于服务器的硬件组成具备多样性，且其中存在大量复杂非线性问题，使其在实际应用中还不够成熟[23]。如在服务器运行状态下AI加速卡、以太网卡、RAID卡等电路单元重复性低，晶体管密度及规模小的器件，由于能够监测的参数不多，导致不容易寻找到合适的预警规律。

服务器中各部件单位时间内所处理的信息量、部件的能耗(或端电流变化)和部件温度是与硬件工作相关的重要参数。信息量是指数据中包含的有效信息的多少，不同的业务数据处理模式可能会产生不同的信息量；能耗是指服务器中各部件在处理数据时所消耗的电能，它与信息量有一定的关系，一般来说处理更多或更复杂的信息需要更高的能耗；温度是指服务器中各部件在运行时所产生的热量，消耗更多电能会导致温度上升。在部件正常工作时，实时监测不同业务类型下的单位时间所处理的业务数据信息量进行离散化取值，并实测对应时间内的部件能耗以及温度变化信息。通过分析这些参数信息的变化规律以及响应的实时性，对它们进行标准化处理得到各业务类型下的样本数据集。本文拟使用ANFIS对服务器不同业务模式下的数据集进行训练建模，并使用训练好的参考模型对硬件参数进行监测，一旦某一部件参数与参考模型输出值相比较持续异常，则对该部件进行硬件异常预警。

1.2 ANFIS结构及参数训练过程

ANFIS是一种实用的人工智能方法，它模仿人类思维来解决不确定问题，具有强大的智能化数据关联、分类和推理能力。作为一种数据学习技术，ANFIS使用模糊逻辑将高度互联的神经网络处理函数和输入特征信息转换为所需的输出。ANFIS结构如图1所示，圆圈表示固定节点，正方形表示自适应节点。ANFIS的结构由五层组成，从输入到输出分别为模糊层、规则层、归一化层、去模糊层和输出层。

图1 ANFIS的结构

在ANFIS中，隶属度函数的参数是通过样本数据集进行训练确定的，隶属度函数相互组合或交互的方式称为规则，这些规则分为前件参数和后件参数[24]，其if-then形式的规则描述如下：

规则 1：

ifx=A1，y=B1，z=C1

thenf1=m1x+p1y+q1z+r1

规则 2：

ifx=A2，y=B2，z=C2

thenf2=m2x+p2y+q2z+r2

规则 3：

ifx=A3，y=B3，z=C3

thenf3=m3x+p3y+q3z+r3

式中，x、y和z是节点的输入；f为输出；Ai、Bi和Ci分别为与输入x、y和z有关的模糊集合，i=1，2，3；mi、pi、qi和ri是结果参数，通常称为后件参数。

第一层：该层称为模糊层，节点函数为隶属度函数，输出值O1，i可以表示为：

(1)

式中，O1，i为该层输出值；n为输入信号数量；μAi、μBi和μCi为广义钟形隶属函数(gbellmf)，定义为：

(2)

式中，ai、bi和ci为前件参数。

第二层：该层称为规则层，节点标记为Π。输出值O2，i是通过所有输入成员函数相乘来计算得到的。

O2，i=wi=μAi(x)μBi(y)μCi(z)，i= 1，2，…，n

(3)

式中，wi表示第i条规则的激励强度。

第三层：该层称为归一化层，节点标记为N。将前一层的输出结果做归一化处理，输出值O3，i是处理后的激励强度。

(4)

第四层：该层称为去模糊层，在归一化的激励强度和结果函数之间创建一个自适应关联函数，O4，i是第三层和第一层的值的乘积。

(5)

式中，mi、pi、qi和ri是结果参数，通常称为后件参数。

第五层：该层称为输出层，标记为∑。它以所有输入信号的总和来计算总输出。

(6)

ANFIS中的模糊隶属度函数参数(包括前件参数和后件参数)是通过大量已知数据生成初始模糊模型再进行训练获得的。在该过程中常用的算法为最小二乘估计(LSE，least squares estimate)方法与梯度下降(GD，gradient descent)法结合的混合算法LSE-GD。

通过这种迭代自适应学习过程对ANFIS进行训练，FIS的前件和后件参数能够被优化调整，最后确定能够拟合训练数据集的隶属度函数参数值。在每次迭代训练中，实际输出与预期输出之间的误差可以被减小，当达到预定的训练次数或错误率时停止训练过程[25]。

2 IQPSO-GA混合元启发式优化算法

在ANFIS模型中LSE-GD为基于导数的优化算法，极易陷入局部最优。元启发式算法在迭代过程引入随机变量，因此有一定概率可以跳出局部最优解，这是其与梯度下降或牛顿拉夫逊迭代最主要的区别。本文提出了一种混合元启发算法IQPSO-GA，能够准确且稳定地获取全局最优解。

2.1 标准的QPSO算法

PSO算法的进化过程从随机解或粒子群的选择开始，每个粒子根据自身的速度、个体极值和全局极值更新自己的速度和位置。粒子的速度与位置的更新由如下方程确定：

(7)

式中，ω为惯性权重，其在算法的全局搜索和局部搜索中起着关键的平衡作用；vi，t表示种群中第i个粒子在第t次迭代时的速度向量。xi，t表示第i个粒子在第t次迭代时的位置向量；Pi，t-1为第i个粒子个体最优位置；Gt-1为整个种群的全局最优位置；c1和c2为加速度常数；r1和r2为[0，1]之间服从均匀分布的随机数。

PSO算法在迭代后期，粒子的速度受到一定限制，不能保证全局收敛。QPSO算法是在标准PSO算法的基础之上，引入量子理论建立的寻优进化算法。主要思想是结合量子行为修改PSO算法中粒子更新位置的方式，具有量子行为的粒子在满足种群空间范围的条件下拥有更加广泛的搜索寻优能力[26]。在QPSO中，粒子位置由以下方程确定：

(8)

(9)

(10)

式中，Mbestt表示在第t次迭代时所有粒子最优位置的平均值；N为种群粒子数；D为粒子维度；pij，t为Pij，t和Gj，t之间的随机位置；Pij，t表示种群第i个粒子的第j维在第t次迭代时的最优位置；Gj，t表示种群的全局最优解的第j维位置；φ1，φ2和uij，t均为[0，1]之间的随机数；xij，t表示第i个粒子的第j维在第t次迭代时的位置；βt为收缩-扩张系数，是用以控制QPSO算法收敛速度的重要参量，通常采用线性减小的方法变化。

βt=0.5(tmax-t)+0.5

(11)

式中，t表示当前迭代次数，tmax表示设定的最大迭代次数。

2.2 改进的QPSO算法

QPSO引入了Mbestt和pij，t的概念，提高了粒子间的协同工作和全局搜索能力，但同时也会影响到粒子的全局搜索效率。为提高粒子搜索效率，我们从粒子最优位置和收缩-扩张系数两方面对粒子位置进行调整。设置第t次迭代时所有粒子最优位置的加权平均值。

(12)

式中，αij，t为每个粒子的权重系数，设置如下

(13)

式中，FGj，t表示全局最优解Gt的第j维对应粒子适应度函数值，Fij表示第i个粒子的第j维的适应度函数值。这样，便可根据全局解和适应度函数值对粒子位置进行调整。

βt为QPSO算法中要控制的参数，在算法运行初期，βt值较大，收敛速度较慢，具有全局搜索能力，而局部搜索能力相对较弱；随着迭代次数的增加，βt值逐渐减小，收敛速度加快，其全局搜索能力相对减弱，而局部搜索能力相对增强[27]。然而在实际应用中，收缩-扩张系数的这种调整方法并不能根据执行过程进行合理的变化，因此需要采用自适应方法调整参数，得到IQPSO算法。

定义误差函数为：

(14)

式中，Fi表示第i个粒子的适应度函数值；FGbest表示全局最优解Gt对应粒子的适应度函数值；可见Error_F表示粒子与粒子群中当前最优位置之间的距离关系。Error_F值越小，表示粒子与当前全局最优位置的距离越近，粒子搜索范围变小，容易趋于早熟；Error_F值越大，表示粒子与当前全局最优位置的距离越远，粒子搜索范围变大，导致收敛速度变慢。基于误差函数Error_F的定义，收缩-扩张系数βt可以被调整如下。

κ=log10(Error_F)

(15)

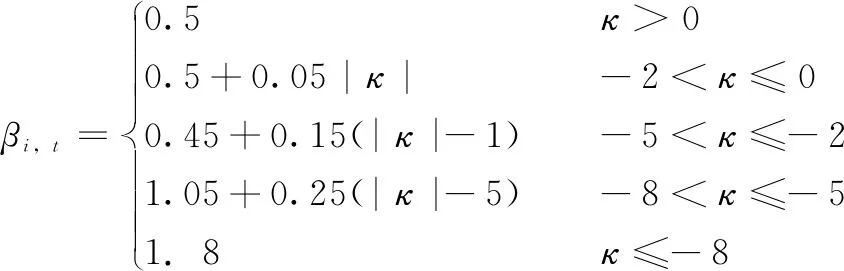
(16)

式中，βi，t表示在第t次迭代时第i个粒子的收缩-扩张系数；当Error_F较大时，应使βi，t取较小值，加快收敛速度；当Error_F较小时，应使βi，t取较大值，扩大搜索范围，避免陷入局部最优。这样，便可将收缩-扩张系数由原来的每次迭代线性减小，更改为在每次迭代中根据误差函数来修正，提高了搜索最优解的收敛速度和精度。

在上述IQPSO算法中，种群粒子的初始化是随机的，在算法迭代的早期阶段，种群搜索存在一定程度的盲区，这不仅降低了算法的搜索效率，也影响了算法的稳定性。此外，随着IQPSO算法的不断迭代更新，种群粒子的多样性减少的问题仍未得到解决。

2.3 IQPSO-GA算法

GA算法通过利用自身的选择算子、交叉算子和变异算子操作，对当前种群中的所有染色体进行更新操作，它具有较弱的局部搜索能力和较低的搜索效率，但在全局最优解的搜索上具有高效性，且具有兼容性高的优点，可以与多种算法结合使用[28]。基于此，本文提出混合元启发式优化算法IQPSO-GA，该算法具备高效的全局和局部搜索能力，算法流程如图2所示。

图2 IQPSO-GA算法流程图

IQPSO-GA混合算法的详细步骤如下所示：

1)设定IQPSO算法中的种群粒子个数和取值范围并赋初值，确定寻优参数的维数和变化范围。

2)将IQPSO算法中当前种群内的全部粒子视作GA算法中的染色体，计算每个染色体对应的适应度值。

3)以适应度值为评价指标，确定是否输出最优粒子。

4)利用IQPSO算法对当前种群中的粒子进行全局的初步搜索，通过式(10)对种群中粒子的位置进行更新。

5)利用GA算法对4)中更新不充分的粒子进行初始化编码，并对编码化的种群粒子进行交叉算子操作、变异算子操作，并计算适应度值。

6)根据5)计算的适应度值产生新的种群，并根据适应度值更新局部最优值Pi，t和种群全局最优值Gt。

7)以达到设定的最大迭代次数或全局最优解误差满足系统需要为终止条件。满足该条件，则输出最优解且算法终止；不满足该条件，则重复4)～ 6)。

3 故障预警模型的建立方法

训练ANFIS隶属度参数的目的是通过调整前件参数和后件参数集合获得具备准确映射能力的ANFIS规则，本文采用混合元启发式算法IQPSO-GA来优化ANFIS参数，建立服务器故障预警模型，实现过程如图3所示。

图3 IQPSO-GA优化ANFIS参数示意图

IQPSO-GA算法优化ANFIS模型的服务器故障预警具体步骤如下所示：

1)在使用优化算法对ANFIS模式进行训练前，需要选取模型期望输出数据集，以及能够输出数据变化的特征信息作为模型输入，本文采用服务器业务与硬件相关的3个关键参数：部件所处理的信息量变化率、能耗变化率以及温度变化率，经过标准化处理后作为预测模型数据。

2)根据收集到的样本数据集中的输入数据和目标输出数据，使用模糊聚类法获得初始FIS结构，确定隶属度函数的规则数量和初始参数，该初始化过程取决于收集到的训练数据集质量。

3)根据2)确定的ANFIS模型初始参数，设置混合优化算法IQPSO-GA中种群粒子个数和取值范围，并对初始粒子进行随机赋值。

4)以粒子所对应的均方根误差，作为该粒子当前适应度值。每个粒子适应度值的适应度函数值计算表达式为：

(17)

5)使用IQPSO更新种群粒子位置，并通过GA算法使粒子之间进行相互交叉和变异，增加种群粒子的多样性。

6)产生一次优化后的聚类参数值作为返回值，更新ANFIS的聚类参数，计算网络误差。

7)以达到设定的最大迭代次数或全局最优解误差满足系统需要为终止条件。满足该条件，生成最终预测模型；不满足该条件，则转至4)。

8)通过7)得到的预测模型，以及经过样本数据训练得到均方根误差，根据经验公式，设置3倍均方根误差为故障预警阈值，实现服务器硬件故障的预警功能。

综上，该方法使用模糊聚类方法设置优化问题，基于收集的训练数据集初始化ANFIS结构，确定规则数量和隶属度初始参数。优化参数包括前件参数和后件参数，它们构成了一组由IQPSO-GA算法调整的变量，以提高ANFIS模型的预测性能。ANFIS模型的预测值产生的均方根误差作为IQPSO-GA算法的适应度值，IQPSO-GA算法的参数设置在后续实验中给出。

4 基于IQPSO-GA-ANFIS的预警模型实验验证

为验证所提基于IQPSO-GA优化ANFIS模型的优越性，以及服务器故障预警方法的有效性，本节使用一组后处理数据集作为样本数据集进行仿真实验。所使用的样本数据集包含3组向量如图4所示，前两组分别为服务器部件所处理的信息量变化率和部件能耗变化率作为输入数据，另一组为部件温度变化率作为输出数据，样本数据集均通过归一化处理映射到0～1之间。实验中所有算法均采用Matlab编码，并在Intel Core i5-9400 CPU@2.90 GH计算机上运行，进行服务器部件数据线下仿真。

图4 样本数据集

数据集中共有500个数据点，各样本数据点为非周期性的采样结果。将数据集分为两部分：第一部分随机取70%的数据点作为训练数据，第二部分取剩余30%的数据作为测试数据。训练数据用来训练模型隶属度参数，测试数据用来检验模型建立的准确性。

实验选择为模糊C-均值聚类方法，表1给出了以迭代次数为终止条件的各优化算法参数设置，这些参数的设置是根据本文团队在试错过程中的经验而选择的。表1中“选择压力”表示GA算法中最佳个体选中的概率与平均个体选中概率的比值；“Gamma”为在GA算法进行交叉操作过程中，设置随机数组时确定的数值范围。文中所提的各元启发算法粒子的编码方式是实数编码，基于采集的服务器样本数据设置算法粒子初始值，每个粒子的位置表示空间中的一个候选解，通常用一个向量表示。同样，每个粒子的速度也会用一个向量表示。在每次迭代中，粒子的速度和位置会根据公式进行更新，更新后的粒子的适应度值会被重新评估，并与个体最优解和全局最优解进行比较，以更新个体最优解和全局最优解。

表1 优化算法参数设置

在本实验中，我们使用预测误差(PE，prediction error)作为主要性能指标，以详细比较基于IQPSO-GA算法训练的ANFIS模型与基于LES-GD混合方法训练的ANFIS模型的预测结果。同时，我们还使用一些众所周知的统计工具作为辅助的寻优评估指标，例如平均预测误差(Error Mean)、误差标准差(ESD，error standard deviation)、平均绝对误差(MAE，mean absolute error)和均方根误差(RMSE)。最后，通过使用决定系数(R2，coefficient of determination)将所提算法与其他元启发式优化算法进行比较。决定系数R2的大小表征回归方程对观测值的拟合程度，取值范围为0～1之间，R2的值越接近1，元启发式算法得到的隶属度参数越准确，即预测值更接近实际值。反之，如果该值接近于0，则说明拟合得到方程的参考价值越低，即获得的隶属度参数的可靠性较低。各性能评价指标公式如下：

(18)

(19)

(20)

(21)

(22)

(23)

基于LES-GD算法与本文所提基于IQPSO-GA优化算法对ANFIS隶属度参数进行训练和测试结果分析如图5和图6所示，两种方法训练后得到的模型分别命名为ANFIS和ANFIS-IQPSO-GA。

图5 ANFIS模型的训练和测试结果

从图5和图6可以清楚地看到，基于IQPSO-GA方法训练的IQPSO-GA-ANFIS模型与LES-GD方法得到ANFIS模型相比，前者具有更好拟合输入-输出数据的能力。通过测试数据分别对两种训练方法得到模型的泛化能力进行检验，结果表明：IQPSO-GA-ANFIS模型的MAE、RMSE分别为0.005和0.011，与传统ANFIS模型的各指标相比，IQPSO-GA-ANFIS模型拟合精度提高了47%以上。同时，由图5(b)和图6(b)中的单步运行时间(Single-step Run Time)可以看到，虽然在训练过程中，ANFIS模型和ANFIS-IQPSO-GA模型的参数求解过程复杂度不同，但完成训练的ANFIS模型与ANFIS-IQPSO-GA模型在进行预测时，具备同样的计算速度，这是因为训练后的两个模型仅是个参数的大小存在变化，其模型复杂度并无变化，故在实际应用时无明显区别。

为充分验证本文所提IQPSO-GA方法的优越性，我们还使用了其他元启发式算法对ANFIS模型的隶属度参数进行训练，如GA、PSO、QPSO、IQPSO、PSO-GA、QPSO-GA。由于元启发式算法初始种群的选取具有随机性，而初始种群的质量对算法寻优过程具有一定影响。故为了验证IQPSO-GA优化ANFIS参数方法的稳定性，我们应用蒙特卡洛统计实验思想，将这些元启发式算法均运行100次，并对100次实验得到的各性能指标的平均值进行比较。在通过训练数据集训练ANFIS模型的过程中，各元启发式优化算法在每一次实验中都会得到一个随迭代次数增加而收敛的适应度函数值，不同元启发式算法得到的平均适应度值的收敛曲线如图7所示。需要注意的是，为进一步说明实验结果并非偶然，我们在每次仿真实验开始前，开源数据集中的所有数据点都会被重新随机排序。

图7 平均适应度值的收敛过程

由图7可以看出，与GA算法相比，PSO算法的适应度函数的收敛速度更快，但由于GA算法具有更强的全局搜索能力，故随着迭代次数的增加，GA算法的寻优精度更高。同时也可以看到，QPSO和IQPSO算法相比PSO算法有更好的收敛速度和精度。这是因为QPSO算法引入了量子行为力学理论，有助于提高粒子相互协作的能力。此外，由于GA算法的兼容性高的特点，将GA算法与其他元启发式优化算法相结合，可以得到寻优性能更好的混合优化算法，如PSO-GA、QPSO-GA和IQPSO-GA。这3种混合优化算法的收敛曲线明显优于单一元启发式算法，其中本文所提的IQPSO-GA算法的寻优性能更为突出。

实验使用测试数据集对通过各元启发式优化算法优化后的ANFIS模型的泛化能力进行了检验，图8为使用测试数据对各优化算法的检验结果，图中圆圈为通过实际值和预测值得到的标记点，直线表示对标记点拟合得到的线性回归方程。

图8 各模型拟合性能的检验结果

对比图8中的各线性回归方程以及R2的值，可以证明通过IQPSO-GA-ANFIS模型得到的预测值更接近实际值，即通过IQPSO-GA优化算法训练得到的IQPSO-GA-ANFIS模型的隶属度参数最准确。通过上述仿真实验，我们比较了不同元启发式算法优化ANFIS参数得到的相应ANFIS模型的泛化能力，验证了IQPSO-GA-ANFIS模型的优越性。

为验证所提基于IQPSO-GA优化ANFIS模型的服务器的故障预警方法的有效性，我们在图4所示样本数据的基础上，添加了若干异常误差(包括高斯噪声与野值噪声)。设置误差值如图9(a)所示，在第450～490组样本数据之间设置了野值突变噪声；通过建立的IQPSO-GA优化后的ANFIS模型预测值与添加误差后的实际值对比结果，以及预测误差分别如图9(b)、(c)所示。

图9 服务器硬件故障预警仿真

图9(a)的曲线为噪声曲线，由该图可以看到，多数误差集中在-0.01～0.01之间，而在第450～490组样本数据中存在大量异常误差，如第455、456、460，464、476、481、484组样本数据中的误差较大，本节以第464和481组样本数据对本文所提方法进行详细说明。图9(b)为使用本文所提方法对实际值的预测结果图，可以看到所提基于IQPSO-GA优化ANFIS模型的故障预警方法可以有效映射部件所处理的信息量变化率、能耗变化率与部件温度变化率之间的动态关系，其中在横坐标为464和481处的预测值与实际值之间偏差较大。为便于分析预测结果以及实时获取监察异常数据，所提方法需处理预测值和实际值之间差值，并根据经验公式，设置3倍的训练时获得的均方根误差为故障预警阈值0.03进行服务器硬件故障的预警，如图9(c)的横坐标464和481处所示，误差分别为0.096 0和0.103 1，远超故障预警阈值。当完成训练的IQPSO-GA-ANFIS模型预测误差超过故障预警阈值时，所提方法可以及时通过输入信息观测部件温度变化率异常。即一旦某一部件能耗或温度持续高于预警阈值，虽然此时部件功能仍可以使用，但需重点关注其接下来的工作状态，对该部件进行硬件异常预警。

5 结束语

本文针对服务器部分业务类硬件无法进行故障预警的难题，通过分析部件相关信息之间的映射关系，建立部件健康状态下的处理信息、能耗、温度变化率之间的动态参考模型，同时从QPSO算法中粒子最优位置求解方法着手，分析了收缩-扩张系数对收敛速度及搜索能力的影响，设计了改进的算法IQPSO，并引入GA的交叉和变异算子操作，提出了一种基于IQPSO-GA混合元启发式算法优化ANFIS模型进行硬件故障预警的方法。实验结果表明，所提IQPSO-GA-ANFIS模型与传统ANFIS模型相比，泛化精度提高了47%以上，验证了所提服务器硬件故障预警方法的有效性和优越性。但在实际应用中仍存在诸多限制问题有待改进，如：1)神经网络的模型训练需要大量样本数据，且训练得到的模型应该随着数据不断更新，仅训练一次便不更新的做法是不现实的；2)温度监测需考虑的指标还有进风风速和温度的影响，本文为保障数据的稳定性暂对其他参数进行了恒定处理。在接下来的工作中将着重围绕上述问题展开研究。