鱼雷射击原理探究式实验平台设计与实现
2024-05-17王平波汪峥嵘徐先勇
代 振, 王平波, 汪峥嵘, 闫 勇, 徐先勇
(1.海军士官学校兵器系,安徽蚌埠 233000;2.海军工程大学电子工程学院,武汉 433012)
0 引 言
声自导鱼雷是水面舰艇最主要的攻潜武器之一。射击原理是讲述如何射击才能使鱼雷发现目标的可能性最大的课程,其核心内容是解算有利提前角和发现概率[1-5]。射击原理课程的教学目标是使学生掌握鱼雷射击方法,并能在实战中灵活运用。然而,射击原理课程的理论性较强,传统的教学方式侧重于理论讲授,实践环节较少,学生理解难度大,导致教学效果有限。因此,射击原理课程教学应当以学生学为中心[6-8],开展高阶的自主探究性教学改革,注重学生创新思维的培养。
搭建探究式实验平台,利用先进信息技术手段辅助课堂教学,可以生动、直观地展示学生难以理解的抽象理论概念,有利于知识的掌握[9]。另外,学生在完成探究式实验的过程中会遇到各类未知问题,涉及的理论与技术也不完全局限于教材。因此,探究式实验平台体现了“做中学”的理念,是一种深入的主动性学习,能增强学生的参与感[10]。Matlab GUI(graphical user interface)仿真平台以其强大的功能、良好的交互性在课堂辅助教学中得到了广泛应用[11-14]。
为了提高课堂教学效果,增强学生的自主创新能力,基于Matalb GUI 开发了鱼雷射击原理探究式实验平台。该平台功能结构采用递进式设计,由易到难,符合学生认知逻辑。学生可在平台上灵活进行参数设置,对射击原理课程主要内容进行自主探究式学习,平台可实时、直观地展示各种处理结果,从而加深学生对重难点知识的理解,提高教学效果。
1 实验基本原理
声自导鱼雷的基本射击原理如图1 所示。图1中,T0点为射击时刻鱼雷的位置,M点为目标的位置,qm为目标的舷角,MN为目标的航向,Ds为目标与鱼雷的距离;鱼雷的自导作用距离为R,自导扇面半角为λ;目标速度为vm,鱼雷速度为vL。
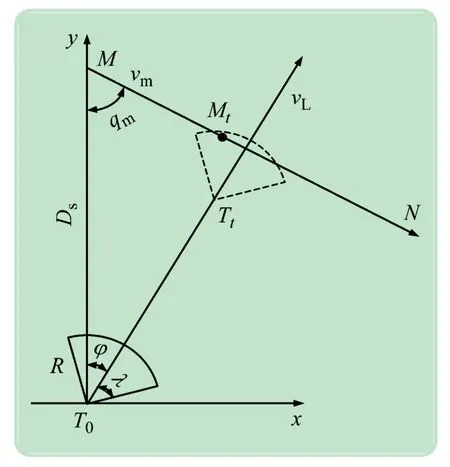
图1 鱼雷基本射击原理
以T0点为坐标原点,以T0M为y轴,建立直角坐标系。若鱼雷射击时,鱼雷自导扇面的中轴线与y轴的夹角为φ(顺时针为正),则φ为声自导鱼雷的射击提前角。
假设经过时间t后,鱼雷运动到Tt点,目标运动到Mt点。若Mt点落在鱼雷的自导扇面内,则为鱼雷发现(或捕获)目标。
声自导鱼雷射击过程中,由于自导扇面的存在,因此存在多个提前角都可以使鱼雷发现目标。考虑到目标和鱼雷自身的各种误差,不同的射击提前角下鱼雷发现目标的概率一般是不同的。通常称鱼雷发现目标概率最高的提前角为有利提前角,记为φa。
鱼雷射击的基本原理就是根据目标和鱼雷自身的性能参数以及环境条件,解算出有利提前角,使得鱼雷以最大的概率发现目标。
2 实验平台总体设计
2.1 功能结构设计
实验平台是探究式平台,目的是引导学生由浅入深,从理论到实践掌握鱼雷射击原理。因此,实验平台的功能结构要有层次性和逻辑性,每一级功能层层递进,上一级功能是下一级功能的前提。实验平台按照基本认知、优化求解和实战运用3 个层次进行递进式功能结构设计。
(1)基本认知功能。在介绍完声自导鱼雷射击基本原理后,很多学生会对射击提前角感到好奇,并设想不按照有利提前角射击,而是任意输入一个提前角,鱼雷还能不能发现目标?因此,探究提前角对鱼雷射击的影响,能激发学生的好奇心,也是平台要具备的基本认知功能。平台从鱼雷对目标的捕获时刻和发现概率2 个方面分析提前角对鱼雷射击的影响,并以仿真推演的形式直观展示分析结果,加深学生的印象。
(2)优化求解功能。学生在基本认知功能尝试之后,发现有的提前角可以使鱼雷发现目标,而有的发现不了,并且即使可以发现目标,不同的提前角对应的捕获时刻和发现概率也往往不同。此时学生会进一步思考,能捕获目标或者发现概率大于零的提前角共有多少,哪个是最优的?这自然而然就引出了有利提前角的概念以及解算方法,所以平台要具有优化求解功能。平台在基本认知功能的基础上,基于捕获时间约束和发现概率约束对有利提前角进行解算。
(3)实战运用功能。学生学习鱼雷射击原理的目的是为了在实战中把鱼雷发射出去,并使得鱼雷尽可能命中目标,所以射击原理的学习要和实战运用相结合。考虑实际的海洋环境对鱼雷自导作用距离的影响,引导学生探究如何在鱼雷自导作用距离不确知的情况下求解最优自导距离,并在此基础上解算有利提前角。
2.2 总体框架设计
实验平台按照学生的认知发展水平以及各功能的内在逻辑关系进行框架设计,主要作用是满足学生对鱼雷射击原理的探究式学习。总体框架分为参数设置、仿真推演和参数解算三大模块,具体如图2 所示。
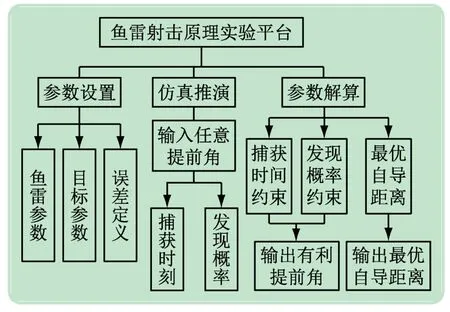
图2 探究式实验平台总体框架
图2 中,参数设置模块用于鱼雷和目标相关参数的设置,并定义可能存在的误差类型与误差大小;仿真推演模块用于直观展示任意提前角下鱼雷捕获时刻或发现概率,便于学生分析提前角对鱼雷射击的影响,促进学生对提前角的基本认知;参数解算模块是仿真推演的深化,提供捕获时间约束和发现概率约束2 种方式优化求解有利提前角。另外,当实际环境下鱼雷自导作用距离不确知时,参数解算模块可以给出最优自导距离,并在此基础上解算有利提前角。
3 实验平台软件实现
Matlab是一款应用广泛的编程软件,内置多种强大的工具箱,可将复杂的算法以简单的函数形式提供给用户,方便系统建模和仿真分析。用户借助GUI,便可以根据自己的想法快速设计仿真平台及软件。下面介绍本平台在Matlab下的实现方案。
3.1 GUI实现
根据实验平台总体框架设计结果构建的平台GUI如图3 所示。在主界面上可以依次实现参数设置-仿真推演-参数解算三大模块的所有功能,并在右侧图像显示区直观展示处理结果。
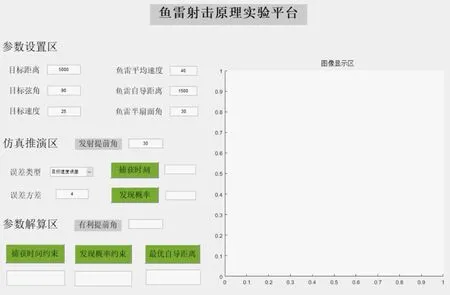
图3 实验平台GUI
3.2 主要功能模块实现
3.2.1 捕获时刻与捕获时间约束
若输入的目标参数和鱼雷参数都没有误差,则基于如图1 所示的直角坐标系,假设t时刻鱼雷和目标的距离为Dt,夹角为λt,鱼雷捕获目标需满足[15]
根据输入的目标参数和鱼雷参数进行仿真,每隔0.5 s判断1 次鱼雷是否捕获目标,如果捕获就记录捕获时刻。鱼雷航行结束,输出第1 次捕获时刻和最后1 次捕获时刻,两者相减就是鱼雷捕获目标的总时间。
捕获时间约束是捕获时刻功能的进一步深化,遍历所有可能的提前角,对每一个提前角都计算其捕获时间。输出结果分为两部分:一是捕获时间大于零的提前角范围;二是捕获时间最长的提前角,即有利提前角。
3.2.2 发现概率与发现概率约束
如果输入的目标参数和鱼雷参数有误差,就根据误差类型和误差方差通过解析法计算鱼雷的发现概率。假设误差类型为目标速度误差,误差服从高斯分布,令目标速度的均值为μ、方差为σ2,则发现概率[4]
其中,vm1和vm2分别为鱼雷能捕获目标时的目标最小和最大速度。
发现概率约束是发现概率功能的进一步深化,同样遍历所有可能的提前角,对每一个提前角都计算其发现概率。输出结果分为两部分:一是发现概率大于零的提前角范围;二是发现概率最大的提前角,即有利提前角。
3.2.3 最优自导距离
参数设置时,通常认为鱼雷的自导作用距离为常数,一般将其设置为良好水文条件下的自导作用距离值,即指标值。实际海洋环境下,不一定都是良好水文条件,在非良好水文条件下,鱼雷的自导作用距离是不确知的,且通常小于其指标值[16],这会导致计算得到的有利提前角偏小,并降低鱼雷的发现概率。
当非良好水文条件下鱼雷自导作用距离不确知时,首先给出自导作用距离的取值范围,然后遍历所有可能的自导作用距离取值,并计算其平均发现概率,使平均发现概率最大的自导作用距离即为最优自导距离。将最优自导距离作为参数输入,即可得到有利提前角。
4 实验流程及示例
4.1 实验基本流程
基于实验平台进行鱼雷射击原理探究式实验的基本流程如图4 所示。
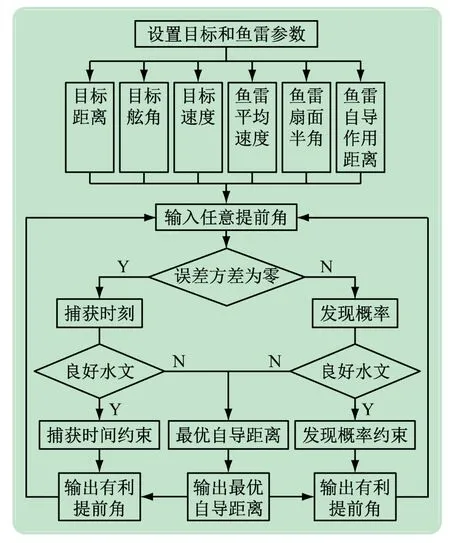
图4 鱼雷射击原理实验流程
学生按照实验流程进行实验的步骤为:
(1)输入目标参数和鱼雷参数,并进行误差设置。
(2)如果误差方差设置为零,就认为输入参数没有误差,可进行捕获时刻分析。分析完成后,如果假定是良好水文条件,通过捕获时间约束就可得到有利提前角。
(3)如果误差方差设置不为零,就进行发现概率分析。分析完成后,若是良好水文条件,则通过发现概率约束得到有利提前角。
(4)若假定不是良好水文条件,也就是鱼雷自导作用距离不确知时,则捕获时间约束和发现概率约束都无法求解有利提起角,此时可求解最优自导距离,并将其作为鱼雷自导作用距离参数重新输入,以获得有利提前角。
(5)得到有利提前角后,将其作为发射提前角输入,以验证有利提前角的最长捕获时间和最大发现概率。
4.2 典型实验示例
仿真参数设置为:目标与鱼雷距离Ds=5 km,目标舷角qm=90°,目标速度vm=25 kn(1 kn =1. 852 km/h),自导扇面半角λ =30°,自导作用距离R=1.5 km,鱼雷平均速度vL=40 kn。
4.2.1 捕获时刻与捕获时间约束
输入射击提前角φ=30°,设置误差类型为目标速度误差,输入误差方差值为零,鱼雷捕获时刻结果如图5 所示,捕获时间约束结果如图6 所示。
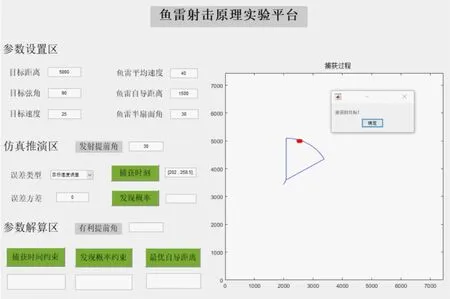
图5 捕获时刻示意图
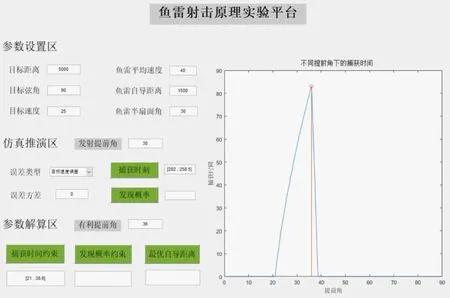
图6 捕获时间约束示意图
图5 中捕获时刻为[202.0,258.5]s,表明鱼雷在该时间段内可以捕获目标,即目标落在鱼雷的自导扇面之内。不同的射击提前角,其总捕获时间不同。从图6 可以看出,当射击提前角在[21.0°,38.6°]范围内时,捕获时间大于零,其中当提前角为36.0°时,捕获时间最长,因此有利提前角为36.0°。
4.2.2 发现概率与发现概率约束
同样,输入射击提前角φ =30°,设置误差类型为目标速度误差,输入误差方差值为4,鱼雷发现概率结果如图7 所示,发现概率约束结果如图8 所示。
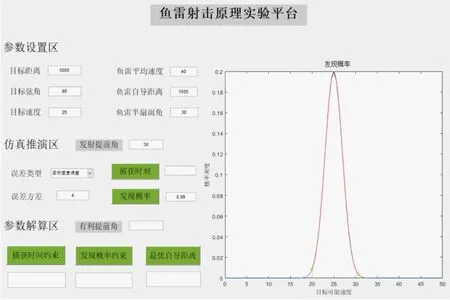
图7 发现概率示意图
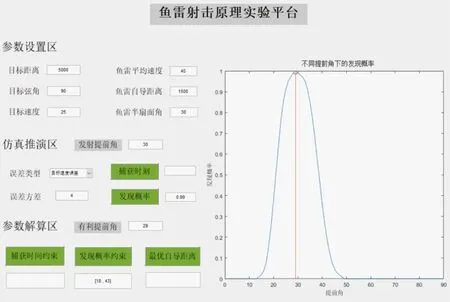
图8 发现概率约束示意图
图7 中,虽然输入的目标速度为25 kn,但是当其误差方差不为零时,表明目标的速度测量是有误差的。假设目标速度服从高斯分布,给定其误差方差值为4,则目标实际的速度可能在[15,35]kn 的范围内(图中蓝线所示)。当目标速度在[20,30]kn 范围内时(图中红线所示),鱼雷可以捕获目标,红色曲线所围成的面积即为发现概率,结果为0.99。不同的提前角对应的发现概率也不同,从图8 可以看出,当射击提前角在[18°,43°]范围内时,发现概率大于零,其中当提前角为29°时,发现概率最大,因此有利提前角为29°。
4.2.3 最优自导距离
当实际环境下鱼雷自导作用距离不确知时,假定其范围为[600,2 000]m,最优自导距离结果如图9所示。将最优自导距离作为鱼雷自导作用距离参数进行输入,射击参数解算结果如图10 所示。
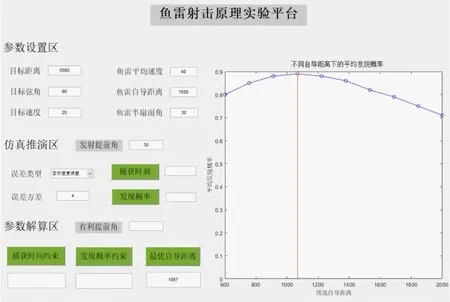
图9 最优自导距离示意图
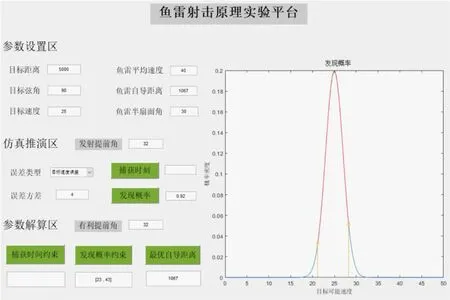
图10 最优自导距离下的参数解算
从图9 可以看出,不同自导作用距离对应的鱼雷平均发现概率不同,当自导作用距离为1 067 m时,平均发现概率最大,即最优自导距离为1 067 m。从图10 可以看出,将1 067 m作为鱼雷自导作用距离的输入参数,通过发现概率约束解算其有利提前角为32°,在射击提前角中输入32°,得到鱼雷的发现概率为0.92。
5 结 语
针对鱼雷射击原理理论性强、难理解问题,基于Matlab GUI设计了一个探究式实验平台。通过该平台,学生可以输入不同参数、设置不同误差类型,形成对鱼雷捕获目标过程的直观认识。在此基础上,学生能充分探究提前角对鱼雷射击的影响,并进一步对提前角进行优化分析,从捕获时间和发现概率2 个维度探索有利提前角的解算方法。此外,学生还可以基于实战场景想定特殊情况,改进有利提前角求解方法。平台功能模块由浅入深,符合学生认知逻辑。
