基于新课标的中小学生计算思维量表构建研究

张屹 陈邓康 付卫东 刘金芳 林裕如 丁双婷

[摘   要] 对学生计算思维的培养已成为数字时代的核心议题，科学、精准的评价则是培养学生计算思维能力的基础。然而，针对义务教育阶段学生的计算思维测评，目前国内尚无依托相关课程标准制定的本土化的、权威的量表。为此，研究首次依托《义务教育信息科技课程标准（2022年版）》（以下简称“新课标”）中的计算思维定义及培养要求，共以12920名（N1=1029，N2=1458，N3=10433）小学生和初中生为研究样本，运用收敛混合方法构建一个面向我国教育实际的、经严格论证的中小学生计算思维量表。结果显示：经过两轮的收敛混合分析，修改后的计算思维量表共包含5个因子及15个题项，具有良好的内容效度；经过大样本实证检验分析，量表具有良好的信效度，且具有跨性别、年级和地区测量等值性，可以用来测量中小学生的计算思维水平。

[关键词] 新课标； 计算思维量表； 收敛混合方法； 大样本实证调研； 义务教育

[中图分类号] G434            [文献标志码] A

[作者简介] 张屹（1967—），女，湖北武汉人。教授，博士，主要从事智慧教育、计算思维教育、教育信息化测评与发展战略研究。E-mail： zhangyi@mail.ccnu.edu.cn。

一、引   言

计算思维（Computational Thinking）指“运用计算机科学的基础概念解决问题、设计系统和理解人类行为的一系列思维活动”[1]，是个体在数字社会生存发展所需要的关键能力[2]。作为21世纪学生的必备素养，计算思维自提出以来就获得了世界各国的高度重视。美国 2011 年修订的《CSTA K-12 计算机科学标准》、英国 2013 年开展的“新课程计划”以及澳大利亚 2015 年制定的“新课程方案”等都强调了对学生计算思维的培养。2022年4月，我国教育部发布《义务教育信息科技课程标准（2022年版）》（以下简称“新课标”），首次在课程标准层面明确指出我国义务教育阶段学生的计算思维培养要求[3]。可见，对学生计算思维的培养已成为数字时代的核心议题。

科学、精准的评价是培养学生计算思维能力的基础，然而，针对义务教育阶段学生的计算思维评价，目前国内尚无依托相关课程标准制定的本土化的、权威的测评量表。近年来，虽然学者们已经形成了一些使用和引证广泛的计算思维量表[4-5]，但这些量表大多改编自国外，其文化适用性和有效性等问题逐渐被国内研究者所关注[6]。课程标准是纲领性的教学文件，对指导学生的能力培养有着不可替代的作用，有学者立足中国教育实际，依托《普通高中信息技术课程标准（2017年版）》，构建了本土化的高中生计算思维评价指标体系[7]。但值得注意的是，发展心理学研究结果明确表示，学生的认知特点和学习需求随年龄增长而有所变化，教学评价也应随这种变化而适当有所反映[8]。因此，对于义务教育阶段学生而言，基于新课标开发更具针对性的本土化计算思维量表显得尤为必要和迫切。

基于此，本研究首次依托新课标中的计算思维定义与培养要求，运用兼顾定性研究与定量研究优势的收敛混合方法开发、验证适切我国当前教育情境的中小学生计算思维测评量表，并通过大样本实证检验确定量表的有效性和适用性，旨在为我国中小学生计算思维的培养、评价以及相关研究提供工具支持。

二、文献综述

（一） 计算思维的定义与测评框架

随着计算思维相关研究在国内外日益升温，学者们对计算思维的解读也呈现出不同的视角[9-10]，但总体上可以分为两类：特定领域视角（Domain-specific）和一般领域视角（Domain-general）。特定领域视角下的计算思维指系统地解决计算机科学或计算机编程主题中的问题所需的特定领域知识或技能[11]，突出强调计算思维与具体学科之间的关系[12]。然而，随着数字时代的不断发展，计算思维不再仅是计算学科关注的重点，学者开始从一般领域的视角出发，将其视为一种普适化的问题解决方法或能力[13]。例如，2011年，周以真教授重新审视计算思维并对其定义做出进一步的澄清，提出计算思维应该被视为一种解决问题的思维过程[14]。国际教育技术协会（ISTE）和计算机科学教师协会（CSTA）也提出了类似的计算思维操作性定义。Selby 和 Woollard则通过综述文献，进一步总结了所有问题解决情境下计算思维的五个基本要素，即抽象、分解、算法思维、评估和概括[15]。

基于一般领域视角下的计算思维概念框架，国内外学者已经开发了一些经典的测评量表[16]。例如：Kukul和Karatas在推理、抽象、分解和概括维度框架内开发了计算思维自我效能感量表[17]；白雪梅和顾小清将Korkmaz等人开发的计算思维量表进行汉化改编，形成了包含5个维度、21个指标的K12阶段学生计算思维量表[6]。但有学者指出，国内外学生所处文化情境不同，国外的计算思维测评量表可能并不完全适用于我国中小学生的计算思维调查[6-7，18]。而课程标准是纲领性的教学文件，对学生的培养和能力评估有着关键的指导作用，因此，国内学者开始基于课标，开发本土化的计算思维测评量表。比如，陈兴冶和马颖莹针对高中学生群体，重点解析我国《普通高中信息技术课程标准（2017 年版）》中的计算思维要求，开发出包含情感态度、合作学习、分解、抽象、概括、算法和评估7个维度的高中生计算思维量表[7]。然而，针对义务教育阶段学生的计算思维评价，目前国内却尚无依托相关课程标准制定的权威测评工具，这可能导致计算思维教育发展的脱节，影响计算思维教育教学质量。

2022年，我国发布的新课标则与一般领域视角相契合，首次从课程标准层面明确了义务教育阶段学生计算思维培养的核心要素，为计算思维测评框架的确立提供了重要依据。新课标明确指出，计算思维是指个体运用计算机科学领域的思想方法，在问题解决过程中涉及的抽象、分解、建模、算法设计等思维活动。此外，具备计算思维的学生还应能够尝试模拟、仿真、验证解决问题的过程，反思、优化解决问题的方案，并将其迁移运用于解决其他问题。重点解析新课标中的培养要求，并结合一般领域视角下的计算思维发展脉络可知，对于我国义务教育阶段学生的计算思维发展而言，以下五个共同的核心要素至关重要：（1）分解，即将一个事物或问题拆分成易于处理的部分或子问题，以促进问题解决的思维过程[19] 。（2）抽象，即隱去问题的细节，关注问题的关键信息[14，19]。（3）建模，即借助一些特定的工具和方法将内在思维过程建立模型，进行可视化表征的认知方法[14]。（4）算法设计，即以序列和规则来思考解决或理解问题的能力[19，20]。（5）评估，即对解决方案不断论证、反思和迭代优化，确保形成一个最恰当、最适合的方案的过程，在该维度下，还对泛化技能进行了测评，即将问题解决方案迁移运用于解决其他问题的能力[21]。本研究将基于上述五因素构成的概念框架，开发相应的计算思维评价指标。

（二） 计算思维测评量表的构建方法

一般来说，测评量表的构建包含以下三个阶段：量表结构的确定与初始题项的生成、量表的验证与修订，以及量表的检验与最终确立[22-23]，且主要基于实证数据采用自下而上的方式[24]，或基于专家审查数据采用自上而下的方式构建量表[25]。随着测评工具相关研究的不断深入，研究者们不断推陈出新，提出了更多高信度与效度的测评量表构建方法，如混合方法（Mixed Method）[26]。混合方法指研究人员综合分析定量数据与定性数据，以保证结论有效性和可靠性的方法。例如：Ya■ci在初始量表的开发阶段，邀请10名专家对题项进行审查以确保内容效度，之后再选取785名高中生开展调研收集定量数据以对量表进行验证与修订，最后形成有效、可靠的高中生计算思维量表[27]；Tsai等人邀请3名教师定性审查初始量表的内容效度后，再以388名初中生为研究对象开展问卷调查，分析定量数据以对量表进行验证与修订，经检验最终量表可作为测量学生计算思维的有效工具[9]。

混合方法虽然已被证实是构建测评工具的有效方法，但许多研究者在应用此方法时只关注量表构建不同阶段间的定性与定量混合，而忽视了某一具体阶段对混合数据的需求。例如，在量表的验证与修订阶段，大多研究仅基于定量的调研数据结果对题项进行删减，然而有学者指出，定性的专家审查在该阶段同样必要以保证其内容效度[26]。De León提出运用收敛混合方法（Convergent Mixed Method），通过召开会议开发初始量表后，在量表的验证与修订阶段，同时收集7名专家的定性审查数据和面向88名研究对象的定量调研数据，收敛分析混合数据以对题项进行修改或删除，最终形成的数字素养测评量表具有良好的信效度[28]。可见，收敛混合方法为我们更好地将混合方法应用于测评量表的构建提供了新的思路。

此外，虽然随着时间的推移，计算思维量表的数量呈现上升趋势，但超过一半量表的信度和效度却并没有得到充分的说明[12]，且少有研究在多个省市开展大样本实证调研以检验最终量表的适用性。陈兴冶强调教育的直接目标是培养人，评价工具中的指标体系也应充分考虑学生的性别、学段、所处地域等诸多因素[7]。因此，在量表的检验与确立阶段，采用大样本实证调研对修改后的量表进行信效度检验和测量不变性检验，可以为量表的有效性和适用性提供更有力的保障。

综上所述，本研究的主要目标是：（1）基于新课标，采用“分解、抽象、建模、算法设计和评估”的计算思维概念框架，运用收敛混合方法构建一个本土化的、经严格论证的中小学生计算思维测评量表；（2）基于大样本实证调研检验所构建量表的信效度，并考察量表在不同性别、年级与地区学生中的适用性，以支持计算思维教育的有效推进。

三、研究过程及方法

本研究的计算思维量表构建过程总体上分为三个阶段：基于新课标的量表初步开发，基于收敛混合方法的量表验证与修订，以及基于大样本实证调研的量表检验与确立。具体过程及方法如图1所示。

（一） 基于新课标的量表初步开发

量表的初步开发包含以下四个步骤：（1）确定概念框架。根据研究需要，我们选取了具有一定研究工作经验、对信息技术教育领域比较熟悉的研究者，组建了一个15人的专家团队，其中包含2位教授、1位副教授、9位博硕士以及3位信息科技学科教师。为确定计算思维的测评维度，专家团队进行了全面的研究回顾和深入的内容分析，并以会议研讨的形式重点解析新课标中的计算思维定义及培养要求，最终提出了计算思维的五个测评要素：分解、抽象、建模、算法设计和评估。（2）生成项目池。基于以上五个要素，检索已有计算思维量表并结合专家的贡献，建立了共包含58个题项的初始项目池。（3）审查题项。专家团队在对项目池的每个题项进行深入审查后，提出了反馈意见，即合并或删除了相似题项。例如，“我通常会为问题找到最有效的解决方案”和“我通常会为问题找到一个快速的解决方案”两项合并为“我能够为问题找到最优的解决方案”。此外，还对部分题项的表述进行了修改。（4）确定初始量表。最终形成包含19个题项的初始量表，并采用李克特5点计分法。

（二） 基于收敛混合方法的量表验证与修订

根据Creswell和Zhou等人关于收敛混合方法的使用建议[22，26]，本研究在量表的验证与修订阶段将同时收集基于专家审查的定性数据和基于试点调研的定量数据，并确定相应的题项标记标准，最后通过收敛分析两种数据的重叠和互补视图，对被标记的题项进行审查、删除或修改。经过两轮的收敛混合验证与修订，专家对量表的认同度和调研数据分析结果逐渐趋同，且量表表现出较高的有效性。

1. 基于试点调研的定量数据收集与分析

（1） 研究对象

本研究在同一省份的W市和H市先后开展了两轮试点调研。第一轮试点调研共计回收有效问卷1029份，其中，男生528人，占51.3%；女生501人，占48.7%；小学672人，占比65.3%，初中357人，占比34.7%。

第二轮试点调研共计回收有效问卷1458份，其中，男生746人，占51.2%；女生712人，占48.8%；小学686人，占比47.1%，初中772人，占比52.9%。

（2） 数据收集与分析方法

本研究采用问卷星与纸质问卷两种方式进行数据收集，针对两轮回收的有效问卷（N1=1029，N2= 1458），我们运用SPSS23.0进行数据整理和分析。本研究的试点调研定量数据分析主要包括两个部分，并针对每个部分确定了相应的题项标记标准：首先，进行题项的区分度分析，主要采用题总相关分析和独立样本t检验两种方式。一般来说，如果個别题项与总分的相关达到显著水平，且系数大于0.4，并且在独立样本t检验中也处于显著水平，则说明该题项具有可接受的区分度，反之，如果不满足上述的任一标准，则对该题项进行标记。其次，进行探索性因素分析。研究采用主成分分析法抽取因子，选择Promax斜交转轴法进行旋转。对于各题项的标记，有以下两点标准：①题项的因子载荷小于0.4；②同时属于多个因子且因子载荷绝对值相近（差异小于0.1）的题项。如果存在以上任一情况，则对该题项进行标记。

2. 基于专家审查的定性数据收集与分析

（1）专家选取

针对义务教育阶段学生计算思维的评价要求，为充分听取不同领域专家的建议，我们邀请了计算思维研究、信息技术课程研究、信息技术教学研究等方面的8名研究者担任专家组成员对量表进行内容审查，专家组成员均对新课标具有深刻理解。

（2）数据收集与分析方法

为了确保计算思维量表构建过程中的内容效度，我们根据De León提到的评估准则形成了专家审查评估工具，要求专家从以下三个方面对量表的每个题项进行评判：①质量，即编写的题项质量高，题项内容能够反映新课标下的计算思维培养要求。②相关性，即题项能够准确反映所属维度的评估内容。 ③清晰度，即题项的表述清晰，不存在容易混淆的术语。专家根据上述标准对每个题项按照五点计分制进行打分，并被要求提出相应的修改建议。最后计算每个题项在以上三个维度上各自的平均值，如果有一个维度上的均值低于4分，则对该题项予以标记。

3. 定性与定量数据的收敛分析

对收集的混合数据进行收敛分析，每个题项存在四类标记结果，并被归纳为三类处理情况（删除、修订和审查）：①在定性和定量分析时均被标记，则该题项予以删除；②仅在定性分析时被标记且专家给出了具体的缘由或修改建议，则参照专家意见进行修订；③ 仅在定性分析时被标记但没有具体的缘由或修改建议，则该题项予以审查，即保留至下一轮验证中再次分析；④仅在定量分析时被标记，则该题项也予以审查。

（三）基于大样本实证调研的量表检验与确立

1. 研究对象

为了确保量表的适用性，本研究面向我国东中西部7个省份（东部：广东省、浙江省；中部：湖南省、湖北省、江西省；西部：贵州省、四川省）开展大样本实证调研。共计回收有效问卷10433份；其中，男生5287名，占比50.7%，女生5146名，占比49.3%；小学6530人，占比62.6%，初中3903人，占比37.4%。

2. 数据收集与分析方法

本次大样本实证调研同样采用问卷星与纸质问卷两种方式进行数据收集，运用SPSS23.0和Mplus7.4对回收的有效问卷（N3=10433）进行分析，主要包含以下三个部分：首先，通过计算Cronbach's α系数和折半信度系数来评估整体量表及分维度量表的信度。其次，对样本进行验证性因素分析，以检验结构效度和聚合效度，从而确定前一阶段建立的量表因素结构是否充分。最后，运用Mplus7.4建构一系列嵌套模型，使用验证性因素分析考察计算思维的多组测量等值性，以确保该量表在不同群体之间具有相同的意义和功能。

四、研究结果

（一）量表的验证与修订

1. 量表的第一轮验证与修订

（1）试点调研结果分析

对第一轮试点调研的数据（N1=1029）进行题总相关分析和独立样本t检验，以分析量表题项的区分度。题总相关分析结果显示，各题项与总分的相关系数位于0.679～0.803之间，且均在0.01水平上达到显著。此外，按总分高低对所有被试进行排序，分为高分组（即得分前27%）和低分组（即得分后27%），对高低分组被试在19个题项上的得分进行独立样本t检验，结果显示，两组被试在每个题项上的得分均差异显著（p<0.001）。两种方法都说明量表所有题项均具有较好的区分度。

之后采用探索性因素分析方法探究计算思维量表的内部维度构成。首先，采用KMO和Bartlette球形检验判断样本数据是否适用于因素分析。结果显示，KMO=0.973>0.9，Bartlett 的球形检验结果达到显著性水平（χ2=11710.403，df=153，p<0.001），综合说明该数据适合进行因素分析。其次，采用主成分分析法提取因子，使用Promax斜交转轴法进行旋转，旋转在10次迭代后收敛。然后，使用探索性序贯设计，采用“逐个指标试验、逐个分析，可下结论即可停止”的方法进行验证性测试，标记载荷值小于0.4或在同一纬度载荷值相近的指标。结果显示，有2个题项（T7和T12）的因子载荷值小于0.4，且有1个题项（T11）在两个因素上的载荷之差为0.02，存在双负荷的情况。对这3个题项进行标记，最终其他题项的因子载荷值位于0.409～0.949，均大于0.4，共扭转出5个因子，累计解释总方差为72.8%。

（2）专家审查结果分析

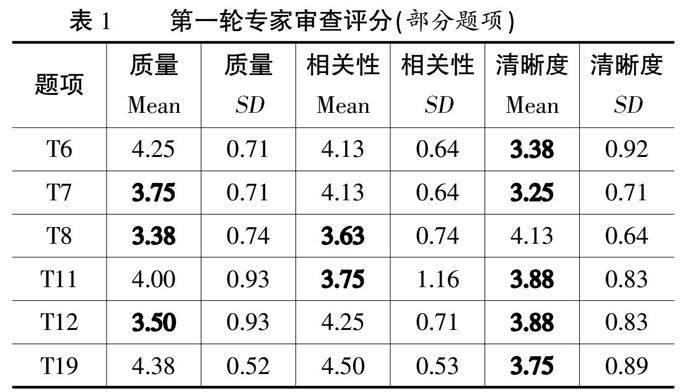
为确保计算思维量表的内容效度，专家组成员仔细审查每个题项，并根据质量、相关性和清晰度三个方面的标准对其进行打分。表1列出了部分題项的专家审查结果。结果显示，在计算思维量表的19个题项中，有6个题项（T6、T7、T8、T11、T12、T19）在三个标准中的至少一个上平均得分低于4，因此被标记，并记录相应的专家建议。

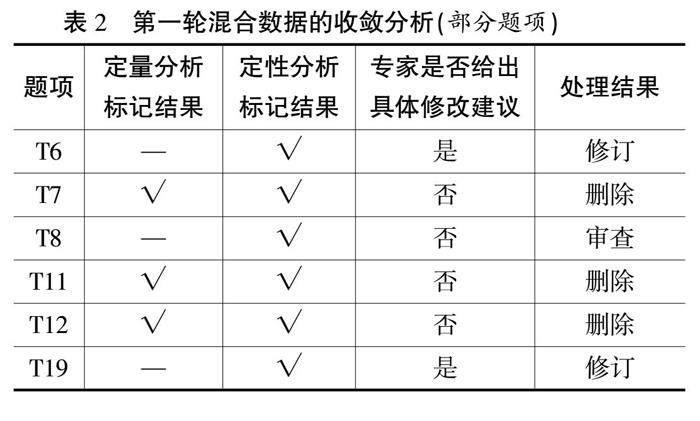
（3）混合数据的收敛分析

通过收敛分析试点调研数据和专家审查数据的重叠和互补视图，确定被标记为“删除、修订或审查”的题项。最终共有6个题项被标记见表2，其中，有3个题项（T7、T11和T12）由于在定量和定性分析阶段均被标记，因此，予以删除；此外，有3个题项（T6、T8和T19）仅在定性分析阶段被标记，其中，题项T6和T19仅在清晰度上的得分较低，且专家给出了具体的修改建议，因此，参照专家意见对这两个题项的表述进行修改，如“T19我能够用某一方法解决其他问题”改为“T19我能够将某一问题的解决方案应用于解决其他问题”；对于仅在定性阶段被标记但没有被提供具体改进信息的题项T8，则予以审查，即直接保留至下一轮验证中被重新分析。

2. 量表的第二轮验证与修订

（1）试点调研结果分析

经过第一轮的验证与修订，计算思维量表还剩余16个题项，我们利用修订后的量表开展了第二轮试点调研（N2=1458）。区分度分析结果显示，各题项与总分的相关系数均在0.5以上（p<0.01），且在独立样本t检验中，高分组和低分组在每个题项上的得分均差异显著（p<0.001），可知所有测量指标均具有较好的区分度。

其次，进行探索性因素分析。结果显示，KMO = 0.942>0.9，Bartlett球形检验χ2（120）=10739.696，p< 0.001，说明该数据满足进行探索性因素分析的前提条件。在此基础上采用主成分分析法提取因子，使用Promax斜交转轴法进行旋转，旋转在6次迭代后收敛。结果发现，所有题项的因子载荷均大于0.4，且不存在双载荷的情况。然而，在第一轮验证中被标记为审查的T8题项与其负荷所在的因素上的其他项目存在语义冲突，且无法进行合理解释，因此，仍然予以标记。最终其他题项的因子载荷值位于0.422～0.921之间（见表3），均大于0.4，共扭转出5个因子，累计解釋总方差为69.6%。

（2）专家审查结果分析

专家审查结果显示，除了在第一轮验证中被标记为审查的T8题项外，其他15个题项在质量、相关性以及清晰度上的平均得分均高于4，说明修改后的量表的内容效度得到了明显提升。

（3）混合数据的收敛分析

通过对第二轮试点调研数据和专家审查数据进行收敛混合分析，最终决定删除T8题项。经过两轮的验证与修订，优化后的计算思维量表共包含15个题项，分别聚合在5个主要因子中，其中，分解维度包含3个题项（T1-T3），抽象维度3个题项（T4-T6），建模维度2个题项（T9-T10），算法设计维度2个题项（T13-T14），评估维度5个题项（T15-T19）。

（二）量表的检验与确立

1. 信度分析

信度分析用于检验收集到的数据结果是否一致，本文采取的检验指标是Cronbach's α系数和折半信度系数。由表4可知，修订后总量表的α值和折半信度系数分别为0.934和0.914，且5个分维度的α值和折半信度系数也都超过了0.7的较高信度标准，表明本研究编制的计算思维量表具有较好的信度。

2. 效度分析

针对探索性因素分析的结果，使用大样本实证调研获得的10433份有效数据和Mplus7.4分析软件进行验证性因素分析，以计算数据的因素载荷量，同时分析其结构效度和聚敛效度。

结构效度指测验某一特定测量工具与其所依据理论或概念框架之间的一致程度[29]。本研究主要通过整体拟合系数来检验量表的结构效度。经计算，标准化残差均方根SRMR=0.016<0.06，近似误差均方根RMSEA=0.026<0.08，Tucker-Lewis指数TLI=0.984>0.9，相对拟合指数CFI=0.988>0.9。综合来看，经过两轮修订优化后的计算思维量表具有良好的结构效度。

聚合效度分析的主要目的在于检验同一变量的各指标之间的相关程度[30]。由表5可知，5个潜变量所对应各个题项的标准化因素载荷范围为0.737～0.859，均大于0.5，说明各潜变量对应所属题项具有较好的代表性。此外，量表5个维度的平均方差提取（AVE）值在0.560～0.716之间，均大于0.5；组合信度（CR）值在0.719～0.864之间，均大于0.7，说明该量表具有良好的聚合效度。

3. 多组测量不变性检验

为了检验量表在不同学生群体中的适用性，我们采用验证性因素分析考察其多组测量等值性。具体通过比较以下三个嵌套模型之间的差异来实现：（1）形态等值，即检验不同群组之间潜变量与指标的从属关系是否相同；（2）负荷等值，即检验因子负荷是否跨组不变；（3）尺度等值，即检验观测变量的截距是否具有不变性。如表6所示，数据结果支持计算思维量表的五维测量结构在性别、年级和地区上的形态等值，负荷等值和尺度等值，且CFI和RMSEA的变化量均未超过建议的临界值（即ΔCFI≤0.01，ΔRMSEA≤0.015）[31]，说明量表在不同性别、年级和地区之间具有相同的意义和功能。

五、结论与讨论

（一）基于新课标确定计算思维测评框架，确保量表的本土化和合理性

本研究基于新课标确定义务教育阶段学生的计算思维测评框架，确保了量表的本土化和权威性，且研究结果显示该量表具有较高的结构合理性。计算思维的评价一直是该领域的重点和难点，尽管近年来国际上相关的测评量表逐渐涌现并得到广泛应用，但其结构是否符合中国化实际和教育情境、是否与时俱进，符合我国最新的计算思维培养要求等问题也日益受到国内学者的广泛关注。课程标准是国家纲领性的教学文件，对学生的发展和能力评估起着关键的指导作用。本研究针对义务教育阶段学生群体，首次依托新课标，提取计算思维培养的五个共同核心要素（分解、抽象、建模、算法设计和评估），在此基础上开发相关测评指标，确保了量表的本土化和权威性。此外，通过验证性因素分析结果可知，各项拟合指数均达到理想标准，说明了该量表的结构具有较高的合理性。

（二）采用收敛混合方法和大样本实证检验构建量表，确保量表的有效性及在不同学生群体间的适用性

本研究严格遵守量表的构建程序，并在量表构建的各个阶段采用合理有效的方法（如收敛混合法、大样本实证检验等），保证了计算思维量表构建过程的科学性和创新性，且其具有一定的可借鉴性。首先，在初始量表的开发阶段，组建专家团队，对计算思维定义进行全面的研究回顾和深入的内容分析，并重点解析新课标，确定计算思维测评的概念框架，经过生成项目池、审查题项，编制了包含19个题项的量表初稿。

其次，运用收敛混合方法对量表进行验证与修订。以往研究在该阶段大多仅基于定量的调研数据结果对题项进行删减，导致量表的内容效度缺乏保证。因此，本研究在将量表用于试点调研以收集定量数据的同时，也收集了基于专家审查的定性数据。在第一轮的收敛混合分析中：（1） 3个题项在定量和定性分析阶段均被标记，因此予以删除；（2） 2个题项仅在定性分析阶段被标记且专家给出了具体的修改建议，因此按照专家意见对其进行修改；（3） 1个题项仅在定性分析阶段被标记且专家没有给出具体的意见，因此保留至下一轮验证中被重新分析。在第二轮的收敛混合分析中，删除1个同时在定量和定性分析阶段被标记的题项。经过两轮的收敛混合分析，优化后的计算思维量表包含5个维度和15个关键指标。

最后，基于大样本实证调研数据，运用信度分析、验证性因素分析等方法检验量表的信效度。研究结果显示，总量表及其5个分维度的α值和折半信度系数均超过了0.7的较高信度标准，说明量表具有较好的信度。另外，本研究还分析了量表的结构效度和聚敛效度。验证性因素分析结果表明，各项拟合指数均达到理想标准，说明量表具有良好的结构效度。量表5个维度平均方差提取值均大于0.5，组合信度均大于0.7，说明其具有良好的聚合效度。

此外，本研究的又一个重要贡献是考察了计算思维量表在不同学生群组中是否具有相同的意义和潜在结构，证明了量表的适用性。我们具体通过比较不同性别、年级和地區分组中，下列三个嵌套模型之间的差异来进行分析：形态等值、负荷等值和尺度等值。结果表明，各模型均达理想的拟合水平，且模型间CFI和RMSEA的变化量均未超过建议的临界值，说明本研究所构建的量表在不同学生群组间具有相同的意义和功能。该量表为我国中小学生计算思维的性别、年级及地区差异研究提供了有效的工具。

六、结   语

本土化的、权威的测评工具是培养学生计算思维能力的基础，也是检验培养成果的重要手段。本研究首次依托新课标，确定计算思维的五因素测评框架，运用收敛混合方法、大样本实证检验构建了最终包含15个题项的中小学生计算思维测评量表。经验证，该量表具有较高的信效度，且具有广泛的适用性。在未来的研究中，可以使用该量表进一步探究我国中小学生计算思维发展的总体水平及群体差异，以及不同群体学生计算思维的影响因素，为研究者和教学实践者制定科学有效的计算思维教育计划提供参考。

[参考文献]

[1] WING J M. Computational thinking[J]. Communications of the ACM，2006，49（3）：33-35.

[2] PEDRO F， SUBOSA M， RIVAS A， VALVERDE P. Artificial intelligence in education： challenges and opportunities for sustainable development [R]. Paris： UNECO，2019：18-20.

[3] 中华人民共和国教育部.义务教育信息科技课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[4] 惠恭健，兰小芳，钱逸舟.计算思维该如何评？——基于国内外14种评价工具的比较分析[J].远程教育杂志，2020，38（4）：84-94.

[5] 房敏，孙颖，吕慎敏，等.基于教学胜任力的师范生计算思维评价量表开发——以斯滕伯格成功智力理论与思维教学理论为支点的探索[J].电化教育研究，2021，42（2）：112-120.

[6] 白雪梅，顾小清.K12阶段学生计算思维评价工具构建与应用[J].中国电化教育，2019（10）：83-90.

[7] 陈兴冶，马颖莹.本土化计算思维评价指标体系的构建与探索——基于1410名高中生的样本分析与验证[J].远程教育杂志，2020，38（5）：70-80.

[8] 孙立会.聚焦思维素养的儿童编程教育：概念、理路与目标[J].中国电化教育，2019（7）：22-30.

[9] TSAI M J， LIANG J C， HSU C Y. The computational thinking scale for computer literacy education[J]. Journal of educational computing research，2021，59（4）：579-602.

[10] 张立国，王国华.计算思维：信息技术学科核心素养培养的核心议题[J].电化教育研究，2018，39（5）：115-121.

[11] 冯友梅，王昕怡，刘晓蕊，等.计算思维不是什么：论计算思维的边界及其何以成为信息技术学科的立足之本[J].电化教育研究，2023，44（1）：84-90.

[12] WEINTROP D， BEHESHT E， et al. Defining computational thinking for mathematics and science classrooms [J]. Journal of science education and technology，2016，25（1）：127-147.

[13] GUZDIAL M. Education paving the way for computational thinking[J]. Communications of the ACM，2008，51（8）：25-27.

[14] WING J. Research notebook： computational thinking—what and why[J]. The link magazine， 2011，6：20-23.

[15] SELBY C， WOOLLARD J. Computational thinking： the developing definition[R]. Southampton： University of Southampton （E-prints）， 2013.

[16] 朱珂，徐紫娟，陈婉旖.国际视阈下计算思维评价研究的理论和实践[J].电化教育研究，2020，41（12）：20-27.

[17] KUKUL V， KARATAS S. Computational thinking self-efficacy scale： development， validity and reliability[J]. Informatics in education， 2019，18（1）：151-164.

[18] 张屹，莫尉，张岩，等.我国小学生计算思维量表研发与应用[J].中国电化教育，2020（10）：49-57.

[19] CSIZMADIA A， CURZON P， DORLING M， et al. Computational thinking—a guide for teachers [M/OL]. Swindon： Computing at school，2015 [2023-11-20]. https：//eprints.soton.ac.uk/424545/. html.

[20] CURZON P， DORLING M， NG T， et al. Developing computational thinking in the classroom： a framework [M/OL]. Swindon： Computing at school， 2014 [2023-11-20]. https：//eprints.soton.ac.uk/369594/. html.

[21] KILI？覶 S， G？魻KO■LU S， ？魻ZT？譈RK M. A valid and reliable scale for developing programming-oriented computational thinking[J]. Journal of educational computing research， 2021， 59（2）：257-286.

[22] CRESWELL J W， CLARK V L P. Designing and conducting mixed methods research[M]. Thousand Oaks， CA， US： Sage publications， 2017.

[23] BURTON L J， MAZEROLLE S M. Survey instrument validity part I： principles of survey instrument development and validation in athletic training education research[J]. Athletic training education journal， 2011，6（1）：27-35.

[24] 张静，刘笛月.社会与情感能力测评三问[J].中国教育学刊，2021（2）：18-24.

[25] NORTH B. Developing descriptor scales of language proficiency for the CEF common reference levels[C]//AIDERSON J C，et al.Common european framework of reference for languages： learning， teaching， assessment： case studies. Strasbourg： Council of Europe， 2002.

[26] ZHOU Y. A mixed methods model of scale development and validation analysis[J]. Measurement： interdisciplinary research and perspectives，2019，17（1）：38-47.

[27] YACI M. A valid and reliable tool for examining computational thinking skills[J]. Education and information technologies， 2019，24（1）：929-951.

[28] DE LE？魷N L， CORBEIL R， CORBEIL M E. The development and validation of a teacher education digital literacy and digital pedagogy evaluation[J]. Journal of research on technology in education， 2023，55（3）：477-489.

[29] CARMINES E G， ZELLER R A. Reliability and validity assessment[M].  Thousand Oaks， CA， US： Sage publications， 1979.

[30] 陳维，黄程琰，毛天欣，等.多维测评工具聚敛和区分效度的SEM分析——以领悟社会支持量表为例[J].西南师范大学学报（自然科学版），2016，41（2）：136-140.

[31] CHEUNG G W， RENSVOLD R B. Evaluating goodness-of-fit indexes for testing measurement invariance[J]. Structural equation modeling， 2002，9（2）：233-255.

A Study on the Construction of Computational Thinking Scale for Primary and Secondary School Students Based on New Curriculum Standards

ZHANG Yi，  CHEN Dengkang，  FU Weidong，  LIU Jinfang，  LIN Yuru，  DING Shuangting

（Faculty of Artificial Inteligence in Education， Central China Normal University， Wuhan Hubei 430079）

[Abstract] The cultivation of students' computational thinking has become a core issue in the digital era， and scientific and accurate assessment is the basis for cultivating students' computational thinking skills. However， there is no localized and authoritative scale based on relevant curriculum standards to measure students' computational thinking in compulsory education. Therefore， for the first time， this study relies on the definition and cultivation requirements of computational thinking in the Compulsory Education Information Technology Curriculum Standards （2022 Edition） （hereinafter referred to as "the new standards"）， takes a total of 12，920 （N1=1029， N2=1458， N3=10433） primary and junior high school students as research samples， and uses the convergent mixed method to construct a rigorously validated computational thinking scale for primary and secondary school students in China. The results show that after two rounds of convergent mixed analyses， the modified computational thinking scale contains 5 factors and 15 items with good content validity. After large-sample empirical test analysis， the scale has good reliability and validity， and has measurement equivalence across gender， grade and region， which can be used to measure the level of computational thinking of primary and secondary school students.

[Keywords] New Curriculum Standards; Computational Thinking Scale; Convergent Mixed Methods; Large-sample Empirical Test; Compulsory Education