源荷不确定对电压稳定性影响的虚拟仿真实验设计

2024-05-15焦提操李震梅张厚升李冠冠

实验室研究与探索 2024年3期

王蕾，焦提操，李震梅，刘洋，张厚升，李冠冠

（山东理工大学电气与电子工程学院，山东淄博 255049）

0 引言

新型电力系统的发展促使电力系统的能源结构发生重大转变，大量可再生能源接入电网，但由于其出力的不确定性和波动性，给电力系统的静态电压稳定和安全运行带来极大的挑战，加之日益增长的负荷需求，电力系统经常运行在极限或稳定边界附近，极易发生系统电压崩溃。电力系统静态电压稳定性是电气工程专业研究生课程《现代电力系统分析》的必修内容和重点授课内容［1-2］，教材中这部分内容围绕经典理论和分析方法展开，少有结合当前电力系统的发展形势，难以满足新工科发展和建设要求。因此在实际教学中需要结合近些年的科学研究成果，探索将科学研究成果融入教学课堂的模式非常重要［3-4］。

为促进科教融合与互助，增进学生对新型电力系统电压稳定性的理解，本文以Matlab 作为仿真工具，设计考虑源荷不确定性的电力系统电压稳定性分析与计算实验教学环节。通过该实验仿真，学生可加深理解电压稳定性的基本概念和分析方法，通过反复运行该实验，学生可测试不同新能源渗透率下源荷不确定性对电力系统电压稳定性的影响、分别测试考虑新能源和/或负荷不确定性对电压稳定性的影响程度等，提升学生的实践能力，锻炼学生的自主思考、主动探索、自主学习和创新能力［5］。

1 算法原理

1.1 连续潮流方法及分岔点类型

静态电压稳定分析理论中，电压失稳对应的静态局部分岔通常包含鞍结点分岔（Saddle-Node Bifurcation，SNB）和结构诱导分岔（Structure Induced Bifurcation，SIB）。考虑发电机无功功率限值时，局部分岔边界上的局部分岔点性质非常复杂，可能包括SNB和SIB。本实验设计将分别研究源荷不确定性对这两类分岔的影响。

连续潮流方法是目前广泛应用的电力系统静态电压稳定性分析实用方法［1-2］。该方法在潮流方程基础上引入连续变化参数和弧长公式，克服了鼻点处潮流方程、雅可比矩阵奇异导致的计算问题，可得电力系统在任一功率增长方向下的P-U（Q-U）曲线，得到电压稳定裕度（即当前运行点至P-U曲线拐点的距离，又称负荷裕度），该指标用于表征电力系统电压稳定的程度。采用该方法计算新能源出力不确定和负荷需求不确定情况下电力系统的负荷裕度。

为直观展示负荷裕度大小，采用功率注入空间的二维局部分岔界面表示电力系统的稳定边界。设节点i的负荷功率因数为cos αi，则负荷随功率因数的变化

1.2 源荷不确定性的建模方法

准确描述系统中源荷不确定性是减小不确定因素影响，提高电力系统安全稳定运行能力的前提。连续潮流方法中，功率增长方向的不确定性可用超棱锥模型表示［6］，源和荷的不确定性可反映为运行点的不确定和功率增长方向的不确定［7］，如图1 所示，运行点的不确定可用一个区域表示，该区域的形状由不确定变量满足的分布函数所决定。初始运行点到局部分岔边界的距离，即为表征电压稳定程度的指标—负荷裕度。

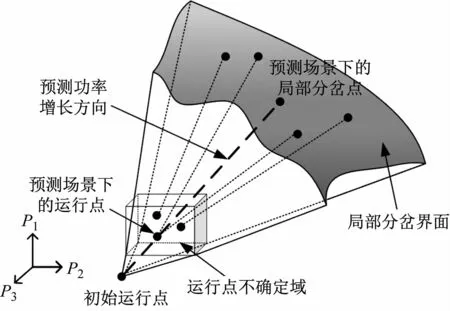
图1 不确定域和局部分岔面示意图

为评估不确定因素对电力系统静态电压稳定性的影响，实验采用基于场景的方法对新能源和负荷的不确定性进行建模。一般情况下新能源和负荷预测存在误差，现有文献中普遍将误差建模为符合零均值的正态分布，因此电力系统中第i个节点上的新能源和负荷预测误差表示为ΔsRi和ΔsLi，即，其中σRi和σLi分别为第i个节点上的新能源和负荷预测误差的标准差。

2 实验设计

2.1 实验目的

源荷不确定性对电力系统电压稳定性的影响分析与测试实验，采用科学研究与课堂教学相结合的方法，其实验教学目的为：

（1）通过文献查阅，熟知新能源出力波动性和随机性对电力系统的影响、建模方法及当前国内外对含大规模可再生能源电力系统的研究方向和研究成果。

（2）能进一步理解电力系统静态电压稳定性的基本原理和分析方法、新能源出力波动性和随机性的建模方法及适用情况，能独立设计实验实施方案并进行结果分析，揭示源和荷不确定性对电压稳定性的影响内在机理。

（3）通过实验方案设计、步骤制定等，鼓励学生体会科学研究全过程，实现发现问题、总结和提炼问题、解决问题方法等过程，锻炼学生实践动手能力和创新思维，提升学生团队协作能力和交流沟通能力、培养精益求精的工匠精神。

2.2 实验测试算例数据

由于大规模电力系统元件众多且非线性强，不利于初次接触该问题的学生对实验内容的理解，课堂上可采用较为简单的电力系统算例进行仿真，教师可将大规模电力系统算例作为课堂教学的延伸，以作业形式布置给学生，鼓励学生进一步探索大规模电力系统中源荷不确定性的影响。

本实验以IEEE 9 节点标准算例为基础修改而成，电网结构、线路及变压器支路参数、负荷及发电机注入功率增长方向如图2 所示，图中数据均为标幺值，容量基准值SB=100 MVA。潮流计算必要的数据参见文献［8-9］，设定1#、2#节点的发电机为常规机组，3#节点的发电机为新能源机组，发电机组的无功功率限值为［-100，100］Mvar，预测3#机组有功功率出力增加0.86p.u.。

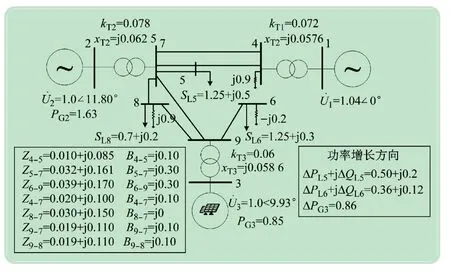
图2 实验算例系统及参数

2.3 实验设计方案与步骤

源与荷的不确定性可反映为运行点的不确定和功率增长方向的不确定，本实验设计了如下测试方案：

方案1运行点相同，只考虑有功和无功功率增长方向的不同。

方案2不计发电机的无功限值，只考虑由于源荷不确定性引起的运行点不同。

方案3不计发电机的无功限值，只考虑由于源荷不确定性引起的运行点和有功和无功增长方向的不同。

方案4计及发电机的无功限值，只考虑由于源荷不确定性引起的运行点不同。

方案5计及发电机的无功限值，同时考虑由于源荷不确定性引起的运行点和增长方向的不同。

本实验实施步骤包括：应用1.2 节中的源荷不确定性建模方法分别产生新能源和负荷的场景，将产生的新能源和负荷场景分别用于上述5 个方案进行仿真测试，测试后汇总各方案下负荷裕度及区间，并分析结果。

3 仿真结果及分析

在不同功率增长方向下，表征电力系统电压稳定性的负荷裕度大小不同。本节仅给出图2 所示功率增长方向下的仿真测试数据，实施本实验教学时教师可以鼓励学生在其他功率增长方向下进行仿真测试。为确保仿真结果的可比性，下述5 个方案的源荷不确定场景均采用同一组数据进行，应用1.2 节不确定性建模方法，对3#节点的新能源机组和5#、6#节点上的负荷分别产生1 000 个随机场景。为方便结果展示，方案2～5 中随机选取其中10 个场景绘制分岔界面。

3.1 方案1 结果及分析

根据图2 中的数据生成仿真算例基础数据，设定负荷功率因数角变化范围为［0°，90°］，各节点的负荷功率按照式（1）、（2）进行变化，分别绘制计及发电机无功限值（Q-limit）和不计发电机无功限值时的电力系统二维局部分岔界面，如图3 所示。

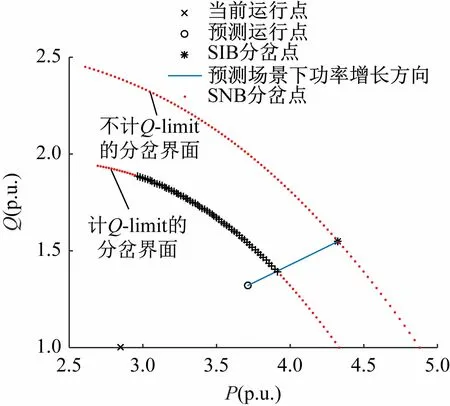
图3 方案1的局部分岔边界

方案1 下，由于只考虑源荷不确定引起的功率增长方向变化，电力系统当前运行点和预测运行点均为固定运行点，功率增长方向不同（即α不同）对电力系统静态电压稳定性的影响不同，具体分析如下：

（1）计及Q-limit 时，电力系统负荷裕度明显减小。在预测场景下（图3 中蓝线），不计Q-limit 时，系统负荷裕度为0.713 2（p.u.），计及Q-limit时，系统负荷裕度仅为0.267 4（p.u.）。

（2）功率增长方向的变化导致负荷裕度和分岔类型发生了较大变化。通常负荷的功率因数大于0.8（即α∈［0，36.9］°），不计Q-limit时，负荷裕度变化范围为［0.492 9，1.211 0］（p.u.），与预测场景下的负荷裕度最大偏差达69.8%；计Q-limit 时，负荷裕度变化范围为［0.085 2，0.657 8］（p.u.），与预测场景的最大偏差可达到146.01%。此外分岔点的类型也不同，即在某些方向上，由于2#号节点发电机和3#节点发电机的无功功率达到了上限，系统发生SIB。

（3）两种情况下得到的预测场景下最差功率增长方向不同（即负荷裕度最小时对应的功率增长方向）。计及Q-limit 时，在α=63°处负荷裕度最小（0.417 2（p.u.）），此方向为最差功率增长方向；不计Q-limits时在α=57°处负荷裕度最小（-0.001 4（p.u.）），此方向为最差功率增长方向。

3.2 方案2、3 结果及分析

方案2 研究源荷不确定引发的运行点变化，功率增长方向不变的负荷裕度变化。方案3 同时考虑了源荷不确定引发的上述两种情况。10 个场景的局部分岔边界如图4、5 所示。

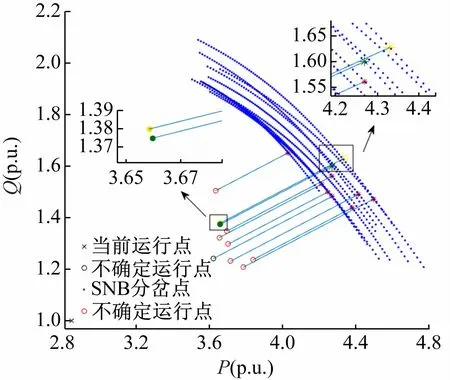
图4 方案2部分场景的局部分岔边界

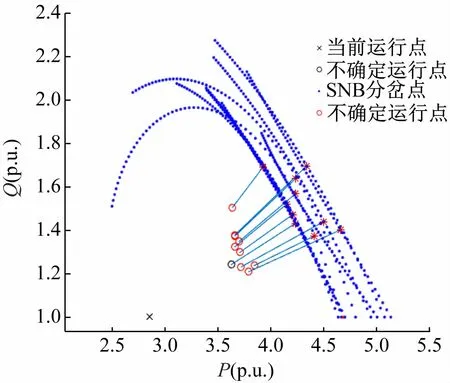
图5 方案3部分场景的局部分岔边界

由于未计及Q-limit，电压崩溃点均为SNB，由图4、5 可以得出：

（1）运行点和功率增长方向的变化与负荷裕度之间具有很强的非线性关系。例如图4 中黄色和绿色所代表场景的运行点距离较小，但距离分岔边界的距离相差很大；

（2）相比方案2，方案3负荷裕度变化区间更大，表明方案3比方案2 更能捕捉到极端场景。方案2 下10个场景的负荷裕度区间为［0.461 1，0.824 5］（p.u.），方案3下负荷裕度区间为［0.366 0，0.926 5］（p.u.）。

3.3 方案4 和5 结果及分析

方案4 只研究源荷不确定性引发的运行点变化时负荷裕度的变化，而方案4 则同时考虑了源荷不确定性引发的上述两种情况。同样地，10 个场景的局部分岔边界如图6、7 所示。

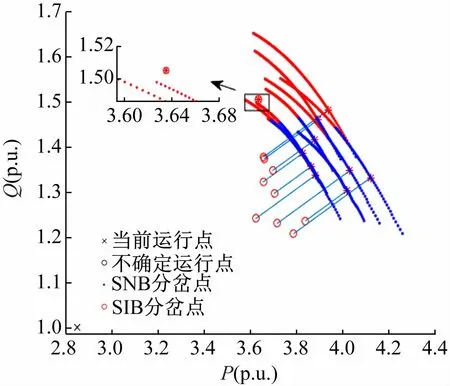
图6 方案4部分场景的局部分岔边界

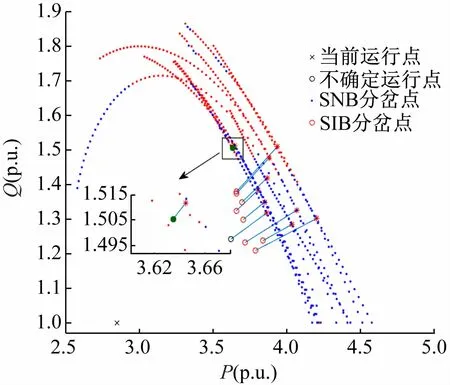
图7 方案5部分场景的局部分岔边界

观察图6、7 可得：

（1）相比于方案2、3，方案4、5 计及了Q-limit，各场景的负荷裕度明显减小。

（2）计及Q-limit时，电力系统可能会因发电机无功越限而使系统不稳定。图中电力系统的分岔边界是由SNB和SIB两种分岔点组成，不同场景下发生的电压崩溃点性质不同。

（3）极端情况下，电力系统可能会因为无功不足而发生崩溃，如图6 中红色的点所示，其运行点与分岔点重合，表明该场景的负荷裕度为零，即该场景下电力系统是电压不稳定的。

3.4 仿真结果汇总及分析

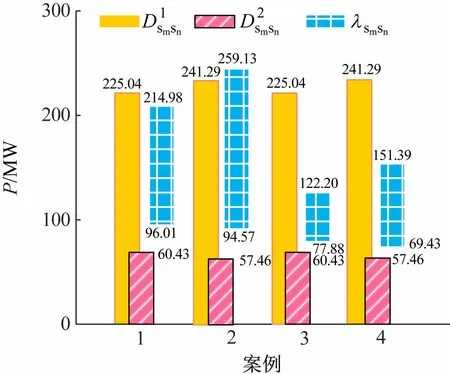
图8 方案2～5下距离指标对比

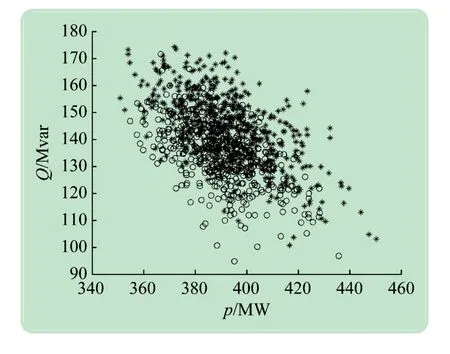
图9 方案5下不同场景的分岔点类型

（1）方案1、3 下各场景运行点距离的范围相同（即［0，225.04］MW），但方案1、3 下的负荷裕度距离的范围相差很大，分别为［96.01，216.48］MW 和［77.88，122.20］MW。

（2）计Q-limit时，方案4、5 相同场景的负荷裕度范围明显小于方案1、2。1 000 个场景中513 个发生SIB（图9 中星号表示），而其他场景发生SNB（图9 中圆圈表示），这意味着源荷不确定性可能导致不同的分岔类型。

本虚拟实验的目的是研究新型电力系统中源荷不确定性对电力系统电压稳定性的影响，通过本实验中5 个方案的仿真及结果分析，可以看出源荷的预测误差对电压稳定性的影响不仅不可忽略，而且源荷不确定性的影响也不能分别单独考虑，需要将新能源和负荷的不确定进行组合，综合考虑运行点的不确定性和功率增长方向的不确定性。

4 虚拟仿真教学环节设计

虚拟仿真教学是理论课堂的有益补充，通过虚拟实验教学可将两者优势互补，更大程度地服务教学。结合本虚拟仿真设计的相关理论知识点和具体特点，本实验适合采用任务驱动式、问题导向法和讨论法相结合的教学方法。实验教学中教师应注重设置问题，用问题启发学生，并逐层递进地加大问题难度，引导学生思考和解决问题［10-12］，可用于设置的问题如下：

（1）研究不同功率增长方向、不同负载程度（重载或轻载）、新能源不同渗透率等情况下，源荷不确定性对电压稳定性的影响程度。教师可通过任务驱动方式给各学生小组布置不同的任务，鼓励学生自主设计和实施实验方案，可以翻转课堂的形式让学生参与汇报，引发学生之间的相互讨论［13］。

（2）考虑新能源出力相关性的影响。新能源出力存在着空间和时间上的相关性，一般来说，其相关性大致可分为线性相关和非线性相关两类。文献［14］中提到Person 相关系数矩阵反映可再生能源之间的线性相关关系，Copula函数能够描述变量之间的非线性相关性。教师可引导学生在进一步实验仿真时，将新能源出力的相关性引入不确定性建模，进一步挖掘其对电压稳定性的影响。

（3）研究如何克服源荷不确定性对电压稳定性的影响。教师通过启发式教学方式，鼓励学生进行文献查阅和综述，查阅文献中对考虑源荷不确定性的电压稳定性分析方法、控制措施和效果进行归纳总结，启发学生开放性思考和深度学习。