结合算子选择的卷积神经网络显存优化算法
2024-05-15魏晓辉周博文李洪亮徐哲文
魏晓辉 周博文 李洪亮 徐哲文

摘要: 针对卷积神经网络训练中自动算子选择算法在较大的显存压力下性能下降的问题, 将卸载、 重计算与卷积算子选择统一建模, 提出一种智能算子选择算法。该算法权衡卸载和重计算引入的时间开销与更快的卷积算子节省的时间, 寻找卸载、 重计算和卷积算子选择的调度, 解决了自动算子选择算法性能下降的问题. 实验结果表明, 该智能算子选择算法比重计算-自动算子选择算法缩短了13.53%训练时间, 比已有的卸载/重计算-自动算子选择算法缩短了4.36%的训练时间.
关键词: 显存; 卷积神经网络训练; 卷积算子; 卸载; 重计算
中图分类号: TP391文献标志码: A文章编号: 1671-5489(2024)02-0302-09
Memory Optimization Algorithm for Convolutional Neural Networks with Operator Selection
WEI Xiaohui, ZHOU Bowen, LI Hongliang, XU Zhewen
(College of Computer Science and Technology, Jilin University, Changchun 130012, China)
Abstract: Aiming at the problem of the performance degradation of the automatic operator selection algorithm in convolutional neural network training under high memory pressure, we modelled offloading, recomputing and convolutional operator selecting in a unified manner and proposed an intelligent operator selection algorithm. The algorithm weighed the time overhead introduced by offloading and recomputing against the time saved by faster convolutional operators, found the scheduling of offloading, recomputing and convolutional operator selecting, and solved the performancedegradation problem of the automatic operator selection algorithm. The experimental results show that the intelligent operator selection algorithm reduces training time by 13.53% over the recomputing-automatic operator selection algorithm and by 4.36% over the existing offloading/recomputing-automatic operator selection algorithm.
Keywords: memory; convolutional neural network training; convolutional operator; offloading; recomputing
由于卷積神经网络卓越的性能, 越来越多的应用使用了卷积神经网络, 如图像识别、 语义分割等. 为加速卷积计算, 研究人员提出了不同的卷积算子, 它们需要不同的工作空间和卷积耗时. 在训练时, 对于卷积算子的选择, 主流的训练框架如Tensorflow[1], 会根据空闲显存自动选择合适的卷积算子. 但卷积神经网络的训练需要保存大量的张量以计算梯度, 训练的显存压力随网络规模的增大而增加. 当显存压力变大, 空闲显存匮乏时, 已有的自动算子选择算法就会选择工作空间需求少但耗时长的卷积算子, 进而延长了训练时间.
目前缓解训练显存压力的主流方法是卸载和重计算张量. 卸载方法[2-5]将显存中暂时不用的张量通过PCIE总线传输到容量更大的CPU内存, 等再次使用时再从CPU的内存传回GPU的显存, 从而缓解训练的存储压力, 运行效率受PCIE总线传输速度的影响. 重计算方法[6-7]保留部分张量作为检查点, 等使用被释放的张量时再从检查点重新计算回来, 运行效率受检查点机制的影响. 通过卸载和重计算释放更多的显存, 本文选择工作空间大但耗时短的卷积算子, 可有效减少训练时间, 但也会引入更多的卸载和重计算时间开销. 所以将卸载、 重计算和算子选择开销统一建模, 并基于开销模型进行综合考虑设计算法已经成为目前该领域重要的研究内容.
本文针对卷积算子选择的问题, 进行整数规划问题的模型设计. 在此基础上, 本文提出智能算子选择算法, 综合考虑卸载、 重计算和卷积算子选择, 使卸载和重计算为更快的卷积算子的工作空间腾出显存, 进而缩短训练时间. 本文使用大规模求解器Gurobi搜索整数规划模型的结果作为建模整数规划问题的可行解, 并将求解器结果转化为显存管理调度, 在训练时通过调度管理显存. 本文对实际AI生产环境下的多种网络进行测试, 并将智能算子选择与自动算子选择进行对比. 实验结果表明, 本文的MO-SOS(memory optimization with smart operator selection)算法可以显著提升GPU运算性能.
1 研究背景
1.1 自动算子选择与卷积神经网络训练显存压力
由于计算量大, 卷积计算是卷积神经网络训练中最耗时的计算. 为加速卷积计算, 研究人员提出了不同的卷积算子实现卷积计算, 如快速Fourier变换卷积[8]和Winograd变换卷积[9]等. 它们在加速卷积计算时需额外的空间保存计算过程中的临时变量, 即神经网络算子的工作空间. 在训练卷积神经网络时, 现有的训练框架如Tensorflow, 会根据空闲显存自动选择合适的卷积算子.
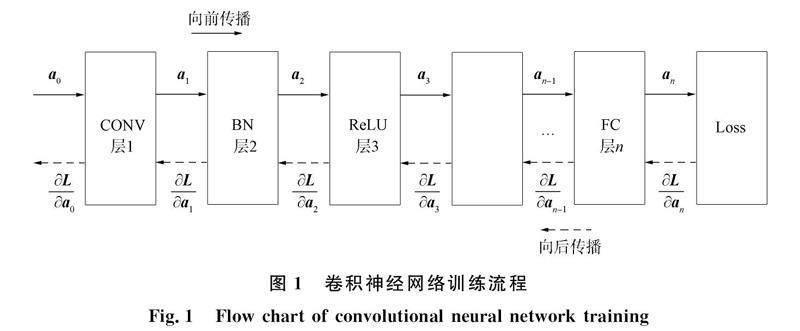
近年来, 卷积神经网络的网络规模越来越大, 使训练的显存压力变得越来越严峻. 训练卷积神经网络是寻找一组网络参数使神经网络的输出尽可能接近期望值. 图1为一个多层卷积神经网络的训练过程, 包括卷积层CONV、 批标准化层BN、 激活层ReLU和全连接层FC等. 目前寻找网络参数常用的方法是梯度下降法, 需要计算神经网络的损失(Loss)和参数的梯度.
Loss是神经网络输出与期望值之间的差距, 这种差距可通过计算损失函数得到, 即图1中的Loss层. Loss是通过前向传播计算的, 前向传播是图1中实线表示的方向. 神经网络训练可通过Loss计算出模型的参数梯度, 从而使用参数梯度更新模型参数.
计算梯度是通过后向传播完成的, 即图1中虚线表示的方向. 计算梯度使用链式法则依次计算出每层的参数梯度. 计算参数梯度依赖张量[WTHX]a[WTBX]i, 所以卷积神经网络训练会保存前向传播的输出张量. 目前, 卷积神经网络通过增加层数以获得更高准确率, 所以它们的训练显存需求也会越来越大, 如Vgg19[10]和Resnet1001等. 当显存压力较大, 空闲显存匮乏时, 自动算子选择算法会选择工作空间少但耗时较长的卷积算子, 增加训练时间. 但卷积神经网络的张量在训练中大部分时间内都是空闲的, 未被访问[2], 所以可将张量卸载或重计算减轻训练显存压力.
1.2 缓解显存压力方案与智能卷积算子选择动机
卸载将CPU的内存作为GPU的缓存, 暂存训练中的张量. 目前的GPU通常作为CPU的外设设备, 它是通过PCIE总线与CPU相连, 它们通过PCIE总线相互传输数据. 由于CPU的内存比GPU的显存容量大, 所以可以把张量卸载到CPU主存, 再次需要张量时预取回GPU显存. 目前的主流显卡如3090,P40等, 都支持计算、 卸载和预取张量并行. 所以为不阻塞训练中的计算, 需要提前卸载或预取张量. VDNN(virtualized deep neural networks)[2]在前向传播中的卷积计算时卸载它的输入张量, 当后向传播需要已卸载的输入张量时再提前预取回. SwapAdvisor[4]通过进化计算选择卸载的张量、 卸载开始时间和预取开始时间, 进一步减少阻塞时间. STR(swap dominated tensor re-generation)[11]发现以前的工作未考虑到多次预取张量, 因为把一个张量卸载到CPU的内存后, CPU的内存中便有了该张量的备份, 当在训练中多次访问这个张量时, STR认为可以把张量多次预取回GPU显存.
随着GPU计算能力越来越强, 张量的卸载和预取的阻塞可能比计算更耗时, 因此研究人员又提出了另一种缓解显存压力的方法——重计算. 重计算保留一部分张量作为检查点, 释放其他的张量腾出显存空间, 当被释放的张量再次需要访问时, 从现有的检查点开始重新计算. 由于引入了重计算, 训练会引入额外的计算时间, 该方法是一种用时间换取空间的方法, 所以保留不同的检查点会引入不同的重计算时间. Chen等[6]把网络分成多个部分, 每部分只保留其输入, 对于每部分的其他张量都重新计算. Checkmate[7]不同于文献[6]的工作, 其探究了在显存容量的限制下, 哪些张量作为检查点能引入最小的额外计算时间, 将重计算问题抽象为线性规划问题, 用现有的求解器解決重计算问题.
卸载和预取会导致额外的阻塞时间, 而重计算会引入额外的计算时间. 文献[12]认为卷积计算时间较长, 不适合用于重计算, 所以卸载和预取卷积计算的输出张量, 而对于激活、 批标准化的输出张量, 它们的计算时间相对较少, 适合用于重计算. 文献[13]研究表明, 以往的卸载和重计算的结合都是以神经网络层的粒度管理显存, 然而一个网络层中也会存在多个计算, 所以提出了张量粒度的显存管理方案. STR认为在非线性卷积神经网络训练时, 一个张量会被多次访问, 所以STR通过多次预取已卸载的张量减少重计算的时间.
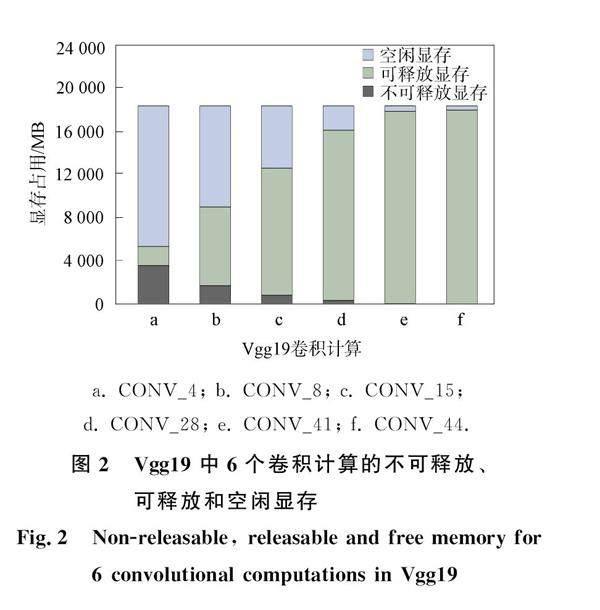
当显存压力较大, 空闲显存匮乏时, 可通过卸载和重计算释放更多的显存, 为卷积算子增加空闲显存. 如图2所示, 它们是Vgg19在Tesla P40平台上训练时的6个前向传播的卷积计算, 使用了主流的CUDNN作为卷积算子库. 不可释放显存是当前卷积计算依赖的输入和输出张量占用的显存, 而可释放显存是暂时不用的张量显存. 与现有的工作相同, 本文主要对前向传播的输出张量进行显存优化, 所以图2只统计了前向传播的输出张量. 在训练时, 卸载和重计算可释放的显存, 为卷积计算腾出空闲显存. 但卸载和重计算会引入更多的额外时间开销, 所以将卸载和重计算引入的时间开销与更快卷积算子节省的时间权衡. 本文拓展了STR的模型, 对卸载、 重计算和卷积算子选择进行统一建模, 寻找卸载、 重计算和卷积算子的调度, 以减少训练时间.
2 问题模型与算法设计
2.1 考虑卷积算子选择的显存优化问题描述
由于深度神经网络框架如Tensorflow和Pytorch等的使用方便与性能强大, 神经网络设计者常使用它们设计和训练网络. 这些主流的框架将深度神经网络的训练过程表示成计算图, 如有向无环图(DAG). 计算图由节点和边组成, 节点表示计算, 如卷积、 矩阵相乘等, 边表示数据依赖, 如图3中的DAG计算图. 在训练时, 训练框架会按照计算图的拓扑排序, 依次执行节点的计算[4,7].
图3中v18节点是Vgg19模型的一个卷积计算, 运行在Tesla P40平台上, 算子库使用了8.0.5版本的CUDNN. 当显存压力变大, 空闲显存匮乏时, 自动算子选择只能选择不需要工作空间但耗时最长的算子Implicit GEMM, 增加训练耗费的时间. 所以MO-SOS算法要通过卸载和重计算为工作空间释放显存, 选择更快的卷积算子. 选择最快的算子Winograd Nonfused, 则需要通过卸载和重计算为工作空间释放约2 GB的显存. 相应地, 卸载和重计算也会引入更多的额外时间开销. 若引入的额外时间开销大于最快卷积算子节省的训练时间, 反而会增加训练时间. 另一种算子的选择是工作空间少但耗时较长的卷积算子Winograd. Winograd算子只需要通过卸载和重计算为工作空间释放约6 MB的显存.
选择最快或最慢的卷积算子都有可能增加训练时间, 所以需要对卷积算子、 卸载和重计算进行统一建模, 寻找一个卷积算子和卸载/重计算的调度, 使得从v1计算节点到vn计算节点执行时间最短. 针对卷积算子的选择问题, 本文从考虑卷积算子选择问题的定义、 卸载和预取建模及工作空间的显存限制三方面进行问题模型的设计.
2.2 考虑卷积算子选择问题的定义
设一个训练计算图为G=(V,E), 其中V={v1,v2,…,vn}表示该计算图有n个计算节点, E表示计算节点之间的依赖关系. 每个计算节点vi的输出需要Mi显存存储输出张量. 每个计算节点vi依赖于其他计算节点的输出vj /St+1,j≤∑aj/v=1Rt,j,v+Pss(t,j),j, t,j,(5)其中: ak表示k计算节点有多少种算子实现; O和P变量表示卸载和预取的决策; 式(2)表示v1到vn计算节点都要计算一次; 式(3)约束了对于不同的计算节点, 算子的选择最多只能有一种. 如上所述, 每个计算节点都依赖于其他计算节点的输出张量. 本文使用卸载和重计算释放显存空间, 在某个节点计算时, 它依赖的张量可能并不存在于显存中, 它可能未重计算或者预取回显存. 所以MO-SOS算法使用St,j变量表示在t阶段时, j张量是否可以访问. 式(4)表示在计算每个节点时它依赖的张量必须可以访问, DEPS[k]表示k计算节点的依赖张量. 而式(5)表示如果在t阶段重計算或者预取回了j张量, 则j张量在之后的计算中能被其他计算节点访问. 2.3 卸载和预取建模 由于卸载、 预取与重计算可以并行, 因此MO-SOS算法可通过卸载和预取减少需要重计算的张量. 但为保证卸载与预取的正确性, MO-SOS算法需要对卸载和预取进行约束. 本文规定在每个节点计算的开端, 开始卸载或预取张量. Ot,j表示在t阶段是否开始卸载j张量, Pt,j表示在t阶段是否开始预取j张量, 则∑n/t=1Ot,j≤1, j,(6) 式(6)表示每个张量只能卸载一次, 因为张量被卸载到CPU内存后, 内存中的张量可作为备份多次预取. 式(7)表示在卸载时张量的数据必须是可以访问的, 否则会传输脏数据. ss(t,i)表示在t阶段完整地卸载或预取i张量, 需要在哪个阶段开始卸载或预取; sf(t,i)表示在t阶段开始卸载或预取i张量, 会在哪个阶段完成. 这两个函数可以根据PCIE总线带宽、 张量大小和每个节点的计算时间计算得出. 但不同的卷积算子耗费不同的卷积时间. 为解决上述问题, 在计算ss和sf函数时, 可根据最快的卷积算子计算, 保证卸载和预取不会阻塞计算. 式(8)表示如果没有预取就不会卸载张量, 且m是可设置的参数. 式(9)表示预取必须在张量卸载完成后开始. 此外, 本文限制了每个阶段只能卸载或预取一个张量, 即Ot,j≤∑ 2.4 考虑工作空间的显存限制 为约束每个节点运行时显存不会溢出, 需要定义一个变量表示每个节点计算时需要的显存. 所以用Ut,k表示在t阶段计算k节点时需要的显存, Ut,0表示在t阶段开始时需要的显存, 它包括模型的输入、 参数、 梯度以及作为检查点的张量Ut,0=Minput+Mparam+Mgrad+∑n/j=1St,jMj+∑(x,y)∈OCC(t)MyPx,y.(14)此外, 预取也会占用显存, 所以OCC(t)表示了哪些张量的预取在t阶段占用显存. 然后递归地计算t阶段每个节点计算时需要的显存Ut,k:Ut,k+1=Ut,k-mem_free(k)+∑ak+1/v=1Rt,k+1,vMk+1+∑ MO-SOS算法希望通过卸载和重计算腾出更多的显存空间, 以选择更快的卷积算子, 进而减少训练时间. 式(2)~(5)保证了重计算的正确性, 式(6)~(13)保证了卸载和预取的正确性, 且式(14)~(18)约束了显存占用. 该问题是难以解决的NP-难问题, 求解空间巨大, 无法通过高复杂度的遍历算法求解, 因此需要有针对性地进行模型设计. 2.5 算法设计 本文问题可以使用求解器根据输入的计算图和GPU的显存限制求解一个可行的方案. 目标公式(1)中的R,S,O,P, Free都是0~1变量, 所以是一个整数规划问题. MO-SOS算法使用现有的求解器去搜索一个可行的结果, 例如Gurobi,Cplex,Scip等. Gurobi是大规模数学规划优化器, 在多个整数规划问题中有更快的优化速度, 适合于本文的最小化问题. 根据Gurobi求解器给出的结果, MO-SOS算法会产生一个显存管理调度L={l1,l2,…,lk}, 其中li是显存管理的操作, 如计算张量、 释放张量、 卸载张量和预取张量. MO-SOS算法如下. MO-SOS算法遍历所有的R,O,P, Free变量去制定显存管理调度. 如果Ri,j,v为1, 则在i阶段, MO-SOS算法要计算j张量, 添加显存管理操作计算张量j到L中, 使用v算子, 即代码10)~12), Algoj表示j节点的算子数量. 如果Oi,k或Pi,k为1, 则在i阶段, MO-SOS算法要卸载或预取k张量, 添加显存管理操作卸载或预取k张量到L中, 即代码4)~6). 如果Freei,j,t为1, 则在i阶段, 计算j张量后, MO-SOS算法释放t张量, 添加显存管理操作释放t张量到L中, 即代码15)~17). 3 实 验 3.1 实验环境 本文选取两种卷积神经网络Vgg19和Unet, 使用C++,CUDA和CUDNN实现Vgg19和Unet的训练, CUDA的版本是11.1, CUDNN的版本是8.0.5. Vgg19在训练时使用数据集Imagenet, 图片大小为227×227, Unet在训练时使用数据集Data Science Bowl, 图片大小为256×256. 它们训练的批次大小分别为144和120. 实验环境采用Ubuntu18.04操作系统, CPU为Intel(R) Xeon(R) CPU E5-2680 v4, 内存为125 GB. 实验使用的GPU为英伟达的Tesla P40, 显存为24 GB, 而PCIE总线的卸载和预取速度分别至少达12 GB/s和11 GB/s. 求解整数规划问题的求解器使用Gurobi, 版本为9.5.2. 本文将智能算子选择算法MO-SOS和自动算子选择算法Auto进行比较. 为能在显存压力较大的情况下进行实验, 给自动算子选择算法配置两种最新的显存优化方法: Checkmate(只有重计算)和STR(卸载和重计算相结合). 这两种显存优化算法与自动算子选择结合后分别为Checkmate-Auto和STR-Auto算法. 本文设置了不同的显存比例, 逐渐减少能使用的显存, 增加训练的显存压力, 测试了Checkmate-Auto,STR-Auto和MO-SOS算法的训练时间. 由于训练是多个训练步组成的, 每个训练步执行时间浮动较小, 所以本文对每个神经网络测试了20个训练步, 取平均值作为每个神经网络一个训练步的执行时间. 本文测试了在不同的显存压力下, 智能算子选择算法和自动算子选择算法训练步的执行时间, 以考察智能算子选择算法能否缩短训练时间. [HT5H〗3.2 实验结果分析 图4为不同算法对Vgg19和Unet一个训练步的执行时间. 由图4可见, 智能算子选择算法在多种显存压力下都优于自动算子选择算法. 本文的智能算子选择算法MO-SOS平均比只有重计算的Checkmate-Auto算法减少了13.53%的训练时间, 比卸载和重计算结合的STR-Auto算法减少了4.36%的训练时间. 在显存比例为0.8和0.7, 显存压力较小时, MO-SOS和STR-Auto算法的训练时间基本相当, 而结合了卸载的MO-SOS和STR-Auto算法仍比Checkmate-Auto算法减少约11.2%的训练时间, 这主要是前者使用卸载减少了需要重计算的张量. 随着显存压力变大, MO-SOS算法的训练时间逐渐比STR-Auto算法减少. 这是因为显存压力变大, STR-Auto算法没有为更快的卷积算子释放更多的显存, 选择了更慢的卷积算子, 增加了训练时间. 但对于Unet网络, 在显存比例为0.4时, MO-SOS与STR-Auto算法的训练时间差距缩小. 不同于Vgg19, Unet是非线性网络, 前向传播的输出张量不仅在后向传播计算梯度时多次使用, 并且在前向传播中也会多次使用. 所以Unet在训练时需要长时间保存多个张量, 导致更大的显存压力, 难以选择更快的卷积算子. MO-SOS和STR-Auto算法训练时间比Checkmate-Auto算法少, 这是因为前者通过卸载减少了重计算的张量. 如图5所示, 在Vgg19训练时, MO-SOS和STR-Auto算法在显存比例为0.7时只有卸载, 而Checkmate-Auto算法只有重计算. MO-SOS和STR-Auto算法通过卸载腾出了足够的显存, 所以它们的卷积计算和其他计算的耗时都明显少于Checkmate-Auto算法. MO-SOS算法训练时间比STR-Auto算法少, 是因为MO-SOS算法卸载和重计算更多的张量以增加空闲显存, 选择更快的卷积算子减少训练时间. 由图5可见, 当显存比例为0.7时, MO-SOS算法比STR-Auto算法卸载的张量更多. 所以MO-SOS算法的卷积计算耗时少于STR-Auto算法. 隨着显存压力增大, MO-SOS和STR-Auto算法逐渐增加了重计算的张量以释放显存. 当显存比例为0.5时, 为给卷积计算的工作空间腾出更多的显存, MO-SOS算法卸载和重计算的张量多于STR-Auto算法. 所以MO-SOS算法的其他计算耗时多于STR-Auto算法, 但MO-SOS算法的卷积计算耗时明显少于STR-Auto算法, 总体训练时间也少于STR-Auto算法. 实验结果表明, 可以通过卸载和重计算为卷积计算增加空闲显存, 选择更快的卷积算子减少训练时间. 在显存压力较小时, 减少的训练时间并不明显. 但随着显存压力增大, 自动算子选择算法的空闲显存逐渐减少, 选择了更慢的卷积算子. 而智能算子选择算法通过卸载和重计算释放了更多的显存, 选择了更快的卷积算子, 进而缩短了训练时间. 综上所述, 针对自动算子选择算法在空闲显存匮乏时会选择工作空间需求少但耗时长的卷积算子, 降低了训练的性能、 增加了训练时间的问题, 本文提出了一种智能算子选择算法, 通过卸载和重计算增加空闲显存. 本文对卸载、 重计算和卷积算子选择进行了统一的整数规划建模, 使用现有的求解器进行求解, 并对多种网络在各种显存压力下进行实验. 实验结果表明, 智能算子选择算法在多种显存压力下优于自动算子选择算法. 参考文献 [1]ABADI M, BARHAM P, CHEN J, et al. Tensorflow: A System for Large-Scale Machine Learning [C]//Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation. New York: ACM, 2016: 265-283. [2]RHU M, GIMELSHEIN N, CLEMONS J, et al. vDNN: Virtualized Deep Neural Networks for Scalable, Memory-Efficient Neural Network Design [C]//2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO). Piscataway, NJ: IEEE, 2016: 1-13. [3]SHRIRAM S B, GARG A, KULKARNI P. Dynamic Memory Management for GPU-Based Training of Deep Neural Networks [C]//2019 IEEE International Parallel and Distributed Processing Symposium (IPDPS). Piscataway, NJ: IEEE, 2019: 200-209. [4]HUANG C C, JIN G, LI J. Swapadvisor: Pushing Deep Learning Beyond the GPU Memory Limit via Smart Swapping [C]//Proceedings of the Twenty-Fifth International Conference on Architectural Support for ProgrammingLanguages and Operating Systems. New York: ACM, 2020: 1341-1355. [5]BAE J, LEE J, JIN Y, et al. FlashNeuron: SSD-Enabled Large-Batch Training of Very Deep Neural Networks [C]//Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation. New York: ACM, 2021: 387-401. [6]CHEN T Q, XU B, ZHANG C Y, et al. Training Deep Nets with Sublinear Memory Cost [EB/OL]. (2016-04-21)[2023-02-01]. https://arxiv.org/abs/1604.06174. [7]JAIN P, JAIN A, NRUSIMHA A, et al. Checkmate: Breaking the Memory Wall with Optimal Tensor Rematerialization [EB/OL]. (2019-10-07)[2023-02-01]. https://arxiv.org/abs/1910.02653. [8]MATHIEU M, HENAFF M, LeCUN Y. Fast Training of Convolutional Networks through Ffts [EB/OL]. (2013-12-20)[2023-02-15]. https://arxiv.org/abs/1312.5851. [9]LAVIN A, GRAY S. Fast Algorithms for Convolutional Neural Networks [C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2016: 4013-4021. [10]SIMONYAN K, ZISSERMAN A. Very Deep Convolutional Networks for Large-Scale Image Recognition [EB/OL]. (2014-09-04)[2023-01-20]. https://arxiv.org/abs/1409.1556. [11]WEN L J, ZONG Z, LIN L, et al. A Swap Dominated Tensor Re-generation Strategy for Training Deep Learning Models [C]//2022 IEEE International Parallel and Distributed Processing Symposium (IPDPS). Piscataway, NJ: IEEE, 2022: 996-1006. [12]WANG L N, YE J M, ZHAO Y Y, et al. Superneurons: Dynamic GPU Memory Management for Training Deep Neural Networks [C]//Proceedings of the 23rd ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. New York: ACM, 2018: 41-53. [13]PENG X, SHI X H, DAI H L, et al. Capuchin: Tensor-Based GPU Memory Management for Deep Learning [C]//Proceedings of the Twenty-Fifth International Conference on Architectural Support for Programming Languages and Operating Systems. New York: ACM, 2020: 891-905. (責任编辑: 韩 啸) 收稿日期: 2023-04-06. 第一作者简介: 魏晓辉(1972—), 男, 汉族, 博士, 教授, 博士生导师, 从事分布式系统、 网格系统与网络安全的研究, E-mail: weixh@jlu.edu.cn. 通信作者简介: 李洪亮(1983—), 男, 汉族, 博士, 副教授, 博士生导师, 从事分布式系统与虚拟化的研究, E-mail: lihongliang@jlu.edu.cn. 基金项目: 吉林省自然科学基金面上项目(批准号: 20230101062JC).
