基于BP神经网络算法的异步电机故障诊断系统研究

孙吴松

摘要：为了确保电机安全可靠地运行，研究了BP神经网络算法对异步电动机进行故障诊断。通过MATLAB平台，分别使用附加动量因子和自适应学习率两种梯度下降法进行网络训练，搭建故障诊断BP网络模型。以MSE值为指标优化最佳隐含层节点数、动量因子与学习率，并通过遗传算法来优化BP网络的初始权值，对故障测试样本进行仿真测试。结果表明，GA-BP网络模型比MF-BP和AG-BP的MSE值更低，仅为0.009 163，优化后的诊断预测结果与目标值几乎没有差别。基于遗传算法改进的故障诊断系统模型能够满足异步电动机故障诊断的应用需求。

关键词：故障诊断；MATLAB；BP神经网络；遗传算法；网络优化

中图分类号：TP183      文献标志码：A      文章编号：1008-4657（2024）02-0001-10

0        引言

随着科技的发展，电机在高铁、磁悬浮列车、飞机电磁弹射装置等新设施上的应用也越来越广泛了，在提供舒适、快捷服务和有力保障的同时，如何确保电机安全可靠地运行，成为人们关注的重要问题［ 1 ］。故障初期的电机，往往会产生诸如机械异常振动和电流信号变化异常等不同形式的异常特征变化，那么利用這些异常变化的特征就可第一时间对电机的故障进行准确地检测和诊断，从而快速、精确地诊断出电动机故障类型及故障部位，从而减少电机维修所花费的时间［ 2 ］。人工神经网络（Artificial  Neural  Network，ANN）的电机故障诊断法是基于反向传播的异步电机故障诊断系统的设计核心，该电机故障诊断法是目前智能化程度相对较高、应用前景也相对较为广阔的一种电机故障诊断法［ 3 ］。其中，反向传播神经网络（Back  Propagation  Neural  Network，BP网络）故障诊断法不只限于完成故障诊断，也能进行故障严重性评估，甚至可以进行故障预测［ 4 ］。BP网络技术从理论上、实践应用上呈现出两种发展趋势：从理论角度上来看，重点依然被放在对网络模型和构成算法的研究上［ 5 ］；从实际应用角度上来看，则重点在使用硬件来制作神经计算机［ 6 ］。

本文以异步电动机为研究对象，基于故障分析和MATLB设计一个基于反向传播算法的异步电机故障诊断系统。在MATLAB中，分别比较附加动量因子和自适应学习率两种梯度下降法构建网络模型的优异性。在此基础上，利用遗传算法（Genetic  Algorithm，GA）将BP神经网络的阈值与权值进行编码，计算适应度，再将适应度符合标准的字符串进行复制、交叉、变异得到新的群体，从而解码得到神经网络最佳权值和阈值。将最佳权阈值代入网络中，从而满足异步电动机故障诊断的需求，提高系统预测的准确性。

1        理论概述

1.1        异步电机的诊断原理

1.1.1        异步电动机的驱动原理

以三相异步电动机为例，当定子绕组上流过三相对称电流，气隙中产生基波旋转磁场，其同步转速与电网频率同绕组极对数有关［ 7 ］。

式中， f1为电网频率；n1为绕组极对数。在短路的转子绕组中，这个基波旋转磁场可用来感应电动势，在转子绕组中产生相应的电流，该电流与旋转磁场相互作用，产生电磁转矩，电磁转矩驱使电动机转动。

1.1.2        异步电机典型故障诊断法

一般来说，异步电机故障经常发生在三个重要组成部分［ 8 ］：①故障发生在定子绕组上；②故障发生在转子上；③故障发生在气隙中。不同种类的电机在不同的工作环境下，可能发生的故障也不尽相同。故障诊断的方法，通常可以根据电机在故障状态下，某一特征参量的异常变化来确定。然而，纯粹地观察单一特征参量的变化很难满足电机故障诊断要求，通过BP神经网络可以诊断非线性故障问题。

1.2        基于BP神经网络的故障诊断技术

1.2.1        BP神经网络基本结构

典型BP神经网络结构分为三层。第一层和第三层分别被称之为输入层以及输出层，第二层则被称之为隐含层。对于BP神经网络的训练和学习可遵循指导性的学习方式来开展。

1.2.2        BP神经网络学习规则

输出层各单元输出值Lt可以由隐含层的输出值bj，连接权值vjt和阈值γt来共同计算得出，然后输出层各单元相应的Ct就可利用Lt并通过传递函数计算得出。

输出层各单元一般化误差值可由网络目标向量及网络的实际输出值计算得出。

位于隐含层的各单元一般化误差值e可以由连接权值vjt，输出层一般化误差值dt以及隐含层输出值bj共同计算得出。

修正连接权值v和阈值γt可使用位于输出层的各单元一般化误差值d及中间层的各单元输出值bj来实现。

连接权值Wij和阈值θj 的修正，可通过使用隐含层各单元一般化误差e，输入层各单元的输入Pk = （a1，a2，…，an）来实现。

在m个学习样本中任意挑选一组作为输入和目标样本，然后返回到隐藏层计算，一直到网络的全局误差E小于先前就已然设定好的一个极小值。

1.2.3        诊断效果评价

利用均方误差（Mean   Square   Error，MSE）评价故障诊断技术及其方法的准确性。

式中，yi为真实值；yi为预测值。

1.3        基于遗传算法优化故障诊断系统

如图1所示，为基于遗传算法优化故障诊断系统流程图。通过遗传算法优化BP神经网络初始的权阈值。在BP神经网络诊断技术的基础上，通过设定遗传算法的初始种群、最大遗传代数、染色体的二进制位数、变异概率和交叉概率计算适应度函数，评估适应度函数的迭代误差。利用复制、交叉、变异等遗传算法提高计算效率和准确度。

2    结果分析

2.1    故障诊断系统建立和训练

2.1.1    训练样本的选取

根据异步电机的典型故障分析可得，输入层神经元为各故障特征频率分量所对应的幅值X = ［X1，X2，…，Xn］和基波分量的幅值之间的比值，输出层神经元为电机的各种不同的故障模式Y = ［Y1，Y2，…，Ym］［ 9 ］。神经元所对应的故障模式可依次为：1.转子发生的绕组故障（短路、断条）；2.气隙发生的偏心故障；3.定子绕组发生的绕组故障（短路、接地）。并以［1，0，0］，［0，1，0］，［0，0，1］作为对应输出层的故障模式。其中，“1”表示有，“0”表示无。将频率分量  f ，（1 + 2S） f ， （1 - 2S） f ， ［1 + （1 -  S） / p］  f ， ［1 - （1 -  S） / p］  f， 3 f ， 5 f 作为输入层神经元。通过计算频率分量所对应的幅值和基波分量的幅值之间比值，并以此值作为网络的输入值。综上，设定要用来搭建诊断系统网络的BP网络为3层网络，输入层神经元数目为7，输出层神经元数目为3。分别采用带有附加动量因子的梯度下降法和学习率可自适应的梯度下降法训练网络。

2.1.2    故障诊断系统模型设计［ 9 ］

将4个标准故障模板X1 ， X2 ， X3 ， X4作为训练样本。

转子绕组故障标准模板X1 = ［1，0.01，0.01，0.009，0.0004，0.003，0.05］；

气隙偏心故障模板X2 = ［1，0.0018，0.0018，0.049，0.041，0.023，0.027］；

定子绕组故障模板X3 = ［1，0.01，0.01，0.134，0.006，0.09，0.027］；

正常模板X4 = ［1，0.01，0.01，0.004，0.004，0.035，0.03］。

样本数据对应的标准输出为转子绕组故障标准输出为Y1 = ［1，0，0］；气隙偏心故障标准输出为Y2 = ［0，1，0］；定子绕组故障标准输出为Y3 = ［0，0，1］；正常无故障标准输出为Y4 = ［0，0，0］。将几组通过实际测量而来的样本X5，X6，X7，X8作为测试样本：

X5 = ［0.89     0.00089    0.00089    0.00356    0.00356    0.03115    0.0267］；

X6 = ［0.9     0.009    0.009    0.0081    0.00036    0.027    0.045］；

X7 = ［0.9    0.00162    0.00162    0.0441    0.0369    0.0207    0.0243］；

X8 = ［0.9    0.0009    0.0009    0.01206    0.0054    0.081    0.0243］。

测试样本对应的标准输出为Y5 = ［0，0，0］，表示正常无故障；Y6 = ［1，0，0］，表示转子绕组故障；Y7 = ［0，1，0］，表示气隙偏心故障；Y8 = ［0，0，1］，表示定子绕组故障。因为理想输出为[0，0，0]，［1，0，0］，［0，1，0］，［0，0，1］，由于输出值为正数时更有利于故障类型的判断，故可选择输出层传递函数为Log-sigmoid函数，选择隐含层的传递函数为sigmoid。

2.2    基于BP神经网络算法的故障诊断结果

2.2.1    隐含层节点的选择

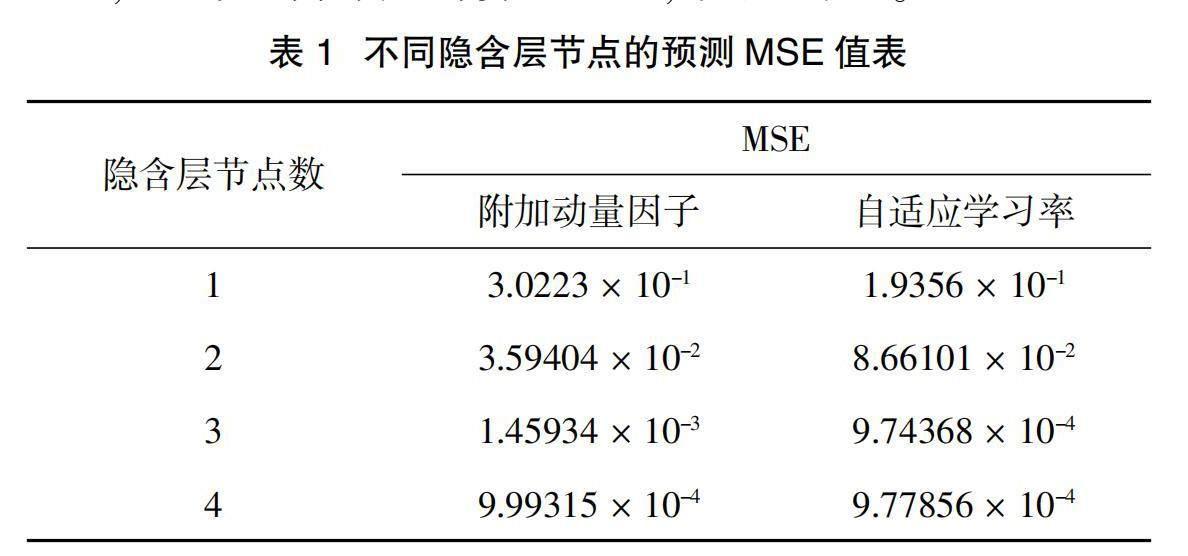
分别使用附加动量因子和自适应学习率的梯度下降法训练方法建立BP神经网络模型，分别为MF-BP（使用附加动量因子的BP神经网络模型）和AG-BP（使用自适应学习率的BP神经网络模型）。其中，隐含层神经元数为15，将训练目标设定为0.001，将学习率设定为0.1，将动量因子设定为0.5，将迭代数最大设定为10 000，最后分别准确地计算出MSE，結果见表1。

BP神经网络的初始权阈值具有很大的随机性，从而很大程度上影响了BP神经网络各方面的性质。由表1中的MSE性能指标，从而确定诊断模型最佳隐含层节点数目分别为10（MF-BP）和13（AG-BP）。

2.2.2     学习率的选择

在最佳隐含层节点数目确定后，以0.01为步长对连续20个不同学习率的BP神经网络进行测试，筛选学习率的最佳取值，得出的测试结果见图2。

通过图2可以得出，可设置最佳学习率分别为0.2（MF-BP）和0.11（AG-BP）。

2.2.3    动量因子的选择

在完成学习率的确定后，对于有动量的梯度下降法的动量因子的数值的确定，以步长0.05不同动量因子的连续19个BP神经网络的动量因子来开展测试，测试将会以值作为测试标准，测试结果见表2。

从表2能够清楚地看到，动量因子可以选取0.05（此时值最小）。综上所述，则可得到经过修正的MF-BP神经网络比AG-BP神经网络的训练模型的MSE值更高。所以后续选择AG-BP神经网络进行优化测试。

2.3    基于遗传算法优化的故障诊断模型

2.3.1    交叉概率的优化

通过遗传算法优化BP神经网络初始的权阈值，参数设定如下：初始种群设定为40，最大遗传代数设定为50，染色体的二进制位数设定为10，变异概率设定为0.01，分别设定交叉概率为从0.65开始，步长为0.05在这五个连续的交叉概率中再选择出一个最优的交叉概率。为提高遗传算法运算速度，均设置较小的种群数量、染色体长度和遗传代数，并将BP神经网络训练目标值设定为0.01，误差用MSE来作为衡量标准，结果见图3～7。

从图3～7能够看出，交叉概率为0.65时，误差最小为9.4 × 10-3，误差进化过程良好，因此交叉概率选用0.65。

2.3.2    测试误差

为了测试不同优化方法对故障诊断系统的准确度的影响，对未进行权阈值初始值优化的BP神经网络（MF-BP和AG-BP）和经过权阈值优化后的BP神经网络（GA-BP）的误差值同时来进行比较分析。将其训练目标设定为0.01，在迭代1 000次后，结果见表3。

由表3可知，GA-BP网络模型比MF-BP和AG-BP的MSE值更低，仅为0.009 163。其次为AG-BP网络模型，MSE值为0.010 428。GA-BP网络模型优化后的诊断预测结果与目标值几乎没有差别，说明该方法对异步电机故障诊断具有更好的效果。因此，基于遗传算法改进的故障诊断系统模型能够满足异步电动机故障诊断的需求。

3    结语

异步电机最典型的三种故障类型为定子绕组故障，气隙偏心故障以及转子绕组故障，这三种故障模式发生时，常带有明显的特征变量的变化。然而，由于故障模式与特征参量之间为复杂的非线性关系，所以引入BP网络来更好地实现这种映射功能。又引进了遗传算法来优化BP神经网络的初始权阈值，从而有效地提高了整个预测模型的预测准确性。通过使用两种梯度下降法来训练网络（附加动量因子和自适应学习率），以期得到更好的故障诊断效果以及更小的误差。利用遗传算法来优化BP网络的初始权值、阈值，从而达到优化模型的目的，结果表明：优化前后的测试误差反差明显。GA-BP网络模型比MF-BP和AG-BP的MSE值更低，表明了选择遗传算法来优化网络模型是可行的。

参考文献：

［1］姚远，李叶松，雷力，等.基于电机驱动系统自传感的机械故障诊断研究综述［J］.电工技术学报，2022，37（12）：2936-2948.

［2］吴国沛，余银犬，涂文兵.永磁同步电机故障诊断研究综述［J］.工程设计学报，2021，28（5）：548-558.

［3］李佩烨.电机故障诊断的智能方法论述［J］.中国设备工程，2021（16）：129-130.

［4］韩亮，郭杰鹏，卢国华.基于改进BP算法的异步电机故障诊断［J］.工业控制计算机，2021，34（2）：71-72.

［5］徐逍帆，葛强.基于BP神经网络的全贯流电机泵故障诊断［J］.内燃机与配件，2021（2）：139-140.

［6］范万里.基于小波分析与BP神经网络的机车牵引电机故障诊断［J］.内燃机与配件，2020（9）：149-150.

［7］陈琼，丁长涛，吕原君.小型三相异步电动机自动装配系统的设计研究［J］.机械设计，2022，39（12）：111-118.

［8］张晟.浅谈三相异步电动机常见故障维修及维护［J］.新疆有色金属，2022，45（6）：97-98.

［9］董建园，段志善.基于 BP 网的异步电机故障诊断方法［J］.西安建筑科技大学学报（自然科学版），1998，（2）：59-62.

Research on Asynchronous Motor Fault Diagnosis System

Based on BP Neural Network Algorithm

SUN  Wusong

（Department of Mechanical and Electrical Technology， Lu 'an Vocational and Technical College， Lu 'an 237158， China）

Abstract：In order to ensure the safe and reliable operation of the motor， the BP neural network algorithm is studied for fault diagnosis of asynchronous motor. Through the MATLAB platform， two gradient descent methods of additional momentum factor and adaptive learning rate are used for network training， and the BP network model for fault diagnosis is built. The MSE value is used as the index to optimize the number of nodes， momentum factor and learning rate of the best hidden layer， and the genetic algorithm is used to optimize the initial weight of the BP network， and the fault test samples are simulated. The results show that the MSE value of GA-BP network model is lower than that of MF-BP and AG-BP， which is only 0.009163. The optimized diagnosis prediction result is almost the same as the target value. The improved fault diagnosis system model based on genetic algorithm can meet the application requirements of asynchronous motor fault diagnosis.

Key words：fault diagnosis; MATLAB； BP neural network; Genetic algorithm; network optimization

［責任编辑：许立群］