数形结合学习策略在小学低段数学教学中的应用

赵崇谕

摘要：数学作为一门较为抽象的学科，对学生的思维逻辑能力有着较高的要求，一些学生对数学的学习存在一定的困难。数形结合学习策略的应用能够将抽象的数学问题具体、形象化，从而降低数学题目的理解门槛，提升学生的学习效率。本文主要以二年级小学数学解决问题为例，对数形结合学习策略在小学数学教学中的应用实践进行了简单阐述，希望能对二年级的教学中数形结合学习策略的应用，起到借鉴作用。

关键词：小学数学 数形结合学习策略 解决问题 应用

一、数形结合学习策略

数形结合，是将数量关系与图形进行有效整合，加以利用，用来分析和解决数学问题的一种方式。

数形结合学习策略是基于数形结合思想，将数形结合应用于具体的数学问题，将抽象的数学问题具体化，将复杂的数学知识简易化，形成一种学习策略。数形结合学习策略是一种利用数字和图形的对应关系将数字、数量关系以及图形等相互转化，从而使抽象的问题直观化，便于学生理解、记忆、解答的方法。

二、数形结合学习策略应用的必要性

数形结合学习策略的应用过程，本质上就是通过“以形助数”以及“以数解形”，实现数形结合。数形结合学习策略的有效利用，既可以培养和锻炼小学生的思维能力和逻辑能力，也可以快速帮助数学初学者，尤其是小学数学初学者快速入门，提高学习效率，提升学习数学的兴趣。同时，巧用数形结合学习策略也能够有效优化小学数学教学。[1]

三、数形结合学习策略助力学生问题解决

（一）读图能力

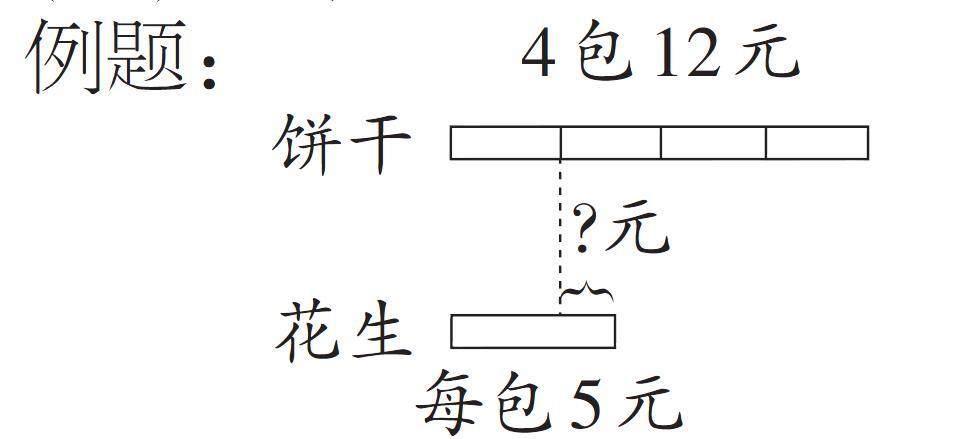
例题：  [饼干][花生][4包12元][？元][每包5元]

问题：每包花生比每包饼干贵多少元？

1.学生们出现的问题情况：（1）12÷4=3（元）

（2）12-5=7（元） （3）4×5=20（元）20-12=8（元）

2.错误成因

（1）读图不完整，只读了一半的问题就着急进行解答。

（2）完全没有读明白题目中的意思。

（3）思考不全面，在得数8出现以后，其实接着想应该再用8÷4=2（元）。

3.读图的方法

（1）建立图和信息间的关系。首先要读信息，然后讀图，最后配合信息读图，在图和信息匹配的基础上理解题意。

（2）理清信息与信息之间的联系。拿饼干和花生的数量关系为例，首先要思考的问题就是饼干和花生二者之间有什么关系。

（3）分析问题和信息之间的关系。找到问号所在的地方，那就是这个题的问题，把问题所表示的意思搞明白，再根据问题去图中找到回答问题所需要的条件。形成解题思路，进行完整答题。

（二）画图能力

例题：如果每个皮球9元，60元最多可以买几个？画一画，算一算。

1.学生们的画图种类及问题情况

（1）[ ]

问题情况：60÷9=5……5；未写单位；未写余数。

（2）[] [] [] [] [] [] [-9][6   15    24   33   42    51   60]

问题情况：下面的数字标注错误；计算结果和图示不照应；画图不完整，未标出数字，且计算时未写出余数；60÷9=5（个）……6（元）；60-9=5（元）。

（3）? ? ? ? ? ?   剩下6元。

出现问题：画图简单，旨意不明；计算结果未写余数。

2.错误成因

（1）书写习惯不好，丢三落四，导致单位和余数缺失。

（2）作图能力有待提高，画图的想法和意图是正确的，但是在作图的过程中，将重要的信息标错，导致结果出现错误。

（3）计算能力有待提高。部分学生在画图的过程中已经将结果画得明明白白，但是计算结果却与作图结果不同，在明知道不同的情况下还不会反思和更正，导致结果错误。

3.画图的方法

（1）读题，找出关键信息。

（2）根据信息规范画图，做到图和信息对应。确保图中能找到所有信息，理清数量关系。

（3）先画出标准量，再画比较量。

（4）图中必须出现问题，即用问号明确指出问题所在。

（三）解题能力（数形结合应用意识）

例题：一家三口人，三人年龄之和是72岁，妈妈年龄是孩子的4倍，爸爸和妈妈同岁，三人各是多少岁？（提示：可以画图帮助解决）

1.学生们的画图种类、问题情况及问题成因

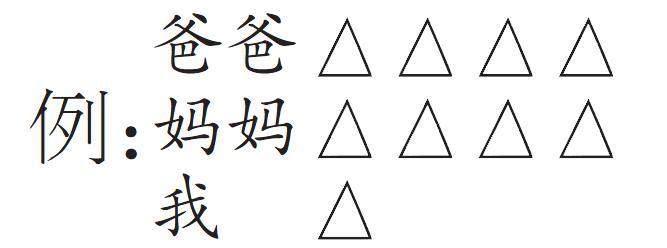
例： [爸爸

妈妈

我]

情况：4×8=32（岁）32+32=64（岁）64+8=72（岁）。经过观察可以看出：学生们画图画明白了，且在画图的过程中，心中已经有了答案。这个题借助画图明显降低了做题难度，但是学生们列的算式却离开了题本身，只凭借图进行了逆向作答。可以看出孩子是懂了，但是列算式作答还需要多加练习。

2.数形结合学习策略应用能力点

（1）要有画图意识。

（2）理清信息，找出关键句、有关系的句子，根据关键句画图。

（3）图画好以后要重新回到题中，把题和图结合思考，运用题中的已知信息和画图后得到的部分信息进行列算式答题。

（4）图和题的关系：图是帮助我们分析清楚题中的信息，并且在已知信息中拓出新的解题思路，从而进一步帮助我们正确答题。

四、结语

小学数学对学生思维能力的发展、数学根基的建设起着至关重要的作用。因此，教师应改善教学方式，提升教学质量，从而使学生的数学学习能力得到提高。数形结合学习策略的有效开展，能够使抽象的问题变直观，复杂的问题变简单，从而降低学生学习数学的难度。还能对学生的解题思维进行拓展，有效促进学生数学核心素养的发展。[2]

参考文献：

[1]冯永明.数形结合思想在小学三年级数学教学中的应用研究[J].文渊，2019.

[2]陈岚.以图促思，渗透数形结合思想[J].教学管理，2020（8）.