不同群桩沉降计算方法在崇明岛水闸工程中的应用分析

章笑 ZHANG Xiao

（上海友为工程设计有限公司，上海 200000）

0 引言

该水闸位于上海市崇明岛南沿，属于长江堤防一线控制口门，采用预制桩基础，按照水闸设计规范的要求需要进行桩基沉降计算。《建筑地基基础设计规范》《建筑桩基技术规范》及上海市地基基础设计标准计算桩基沉降的主要方法都是单向压缩分层总和法，但是关于土中附加应力的计算方法尚不统一，本文通过各方法的计算沉降结果与实测成果对比分析，研究各方法在本地区的适用性。

1 群桩沉降计算理论

1.1 群桩的沉降特性和影响因素

群桩效应不仅对于桩侧、桩端阻力的发挥有重要影响，更重要的是影响桩基沉降。常规桩距条件下，由于桩基应力叠加导致桩端平面以下的应力水平相较于单桩明显提高，压缩层厚度随之加深，导致群桩的沉降量和延续时间都明显大于单桩。

总体而言，群桩的沉降由桩间土压缩变形和桩端沉降组成，这两种变形占总沉降量的比例同土体性质、桩基布置形式、荷载作用方式、成桩工艺及承台等因素有关。

对于均匀的黏性土，桩端沉降占比随土质变硬而增大；随着桩间距的增大，桩端沉降占比逐渐减小，桩间土的压缩变形随桩距增大而增大，当桩距超过6 倍桩径时，群桩沉降以桩间土的压缩变形为主；对于小桩距群桩（2～3 d）在工作荷载下，桩间土基本不发生竖向压缩（粉土）或者在桩端以上1/3～1/4 桩长范围发生一定压缩变形（软土），而对于大桩距群桩，加载时即出现桩间土压缩；随着桩土模量比的增加，总沉降逐渐减小，而桩端沉降反而有所增加，桩间土的压缩变形占比急剧减小，当桩土模量比大于500 时，桩间土压缩变形占比已经很小，常规设计的桩基，桩土模量比在500～3000 之间，桩身压缩占比很小，群桩沉降主要由桩端沉降组成。

由此可见，群桩沉降是一个非常复杂的问题，受多方面因素的影响，目前还没有一种适用于所有情况的通用的群桩沉降计算方法，多是半理论半经验方法。

目前主流的群桩沉降计算方法可分为三类：第一类是等代墩基法（等代实体深基础法），基于Boussinesq 解，根据假设条件的不同可分成不同的计算模式，目前国家地基规范和桩基规范均有采用该方法；第二类是Geddes 法，基于Mindlin 解，目前国家桩基规范对于单桩沉降计算采用考虑桩径影响的Mindlin 解，国家地基规范则可将其用于群桩沉降计算并且不考虑桩径影响；第三类是桩筏基础的整体分析方法，比如有限元法、弹性法等，但是该法建模复杂，难以合理确定岩土的本构模型，计算参数多、计算量大，导致其难以在实际工程中得到广泛应用。本文主要研究规范推荐的前两种简化分析法。

1.2 等代墩基法（实体深基础法）

对于桩距不超过6 倍桩径的群桩基础，假设桩端以上的群桩内部不出现桩土相对位移，如同实体墩基，其沉降计算方法采用单向压缩分层总和法，与浅基础相同。

以桩端作为等代基底面，不考虑桩间土的压缩变形，认为桩基变形完全由桩尖以下的土体整体压缩引起，等代基底面以下土中的附加应力采用Boussinesq 解计算。沉降计算公式为：

式中m=l/b，n=z/b，l、b 分别为矩形基础的长短边，z 为从基底起计算点的深度。其他各参数含义详见《建筑地基基础设计规范》（GB50007-2011）5.3.5 条，不再赘述。

针对基底附加应力p0的计算分为两种模式：

模式一：不考虑附加应力沿桩基侧面的扩散，计算基底在桩端，基底面积为群桩边桩外缘包围的面积。墩底附加应力为承台底面的附加荷载F 除以墩底面积，即：

模式二：考虑附加应力沿桩基侧面以φ/4 角度的扩散，扩散线与桩端平面相交围成的面积为等代墩底面积，则墩底附加应力为：

式中a、b 分别为边桩外缘包围尺寸的长宽，φ 为桩长范围土的内摩擦角加权平均值，L 为桩入土深度。

等代墩基法存在以下问题：

①忽略了桩间土的压缩变形，当桩间土压缩量较大时不适用，比如桩端桩侧土层相同时，特别是软土中的大桩距桩基，桩间土的压缩变形较大且无法忽略。

②墩底（桩端）平面以下土中的应力采用Boussinesq解计算，该解为半无限体受表面荷载的解答，与实际桩基受力后应力向土体内部扩散的解答不同，应力计算结果偏大。

③由于采用Boussinesq 解计算的土中应力偏大，导致压缩层深度随之偏大，压缩模量取值也偏大。

④该法对于布桩不规则、桩长不同的稀疏群桩，其计算误差较大且规律性差。

⑤桩端附加应力取承台底平均附加应力，忽略了承台底附加应力向水平方向的扩散作用，实际桩端的附加应力小于承台底附加应力。

1.3 基于Mindlin 课题的Geddes 桩基沉降计算法

Mindlin 解是在弹性半无限体空间内部作用有一单位集中力时，在半无限体内部任一点引起的竖向应力和位移，因为桩基沉降的计算荷载均作用在地基土内部，因此用Mindlin 解代替半无限体受表面荷载的Boussinesq 解求解桩端以下土层的附加应力更为合理。

Geddes 基于弹性理论的Mindlin 应力公式积分后得出单桩荷载在半无限地基中产生的应力，用简单叠加原理求得群桩荷载在地基中产生的应力，然后再按分层总和法原理计算沉降，该方法可方便地考虑桩基布置型式、不规则布桩及不同桩长等因素对沉降计算的影响。

Geddes 法将桩端压应力简化为作用于桩轴线的集中力、将桩侧剪应力分别简化为作用于桩轴线沿深度呈均匀分布和三角形分布的集中力。相当于将桩顶总荷载Q 分解为三部分：①桩端集中力Qp=αQ；②沿深度呈均匀分布的侧阻力Qsr=βQ；③沿深度呈三角形分布的侧阻力Qst=（1-α-β）Q，其中α、β、（1-α-β）分别为桩端阻力、桩侧均匀分布摩阻力和桩侧三角形分布摩阻力的荷载分担系数。土中任一点的竖向附加应力σz可通过叠加求得，σz的表达式如下：

式中Ip、Isr、Ist分别为桩端阻力、桩侧均匀分布摩阻力和桩侧三角形分布摩阻力按Mindlin 解计算的竖向应力系数，其与桩入土深度、计算点与桩身轴线的距离、计算点与承台底面的距离、土的泊松比有关。

群桩沉降计算公式为：

式中各参数含义详见《建筑地基基础设计规范》（GB50007-2011）附录R。

Geddes 法只适用于桩间距较小且各桩受力均匀的常规桩长的情况。首先，将桩端阻力和桩侧阻力均简化为集中力，忽略了桩径的影响，计算的桩端平面以下应力偏大，在桩端平面以下存在应力集中现象，特别是桩端以下1/10桩长范围内偏离程度很大，导致Geddes 法不能用于单桩和桩数较少的群桩计算，因单桩压缩层厚度较小，其受到的影响较大，使计算值明显偏大。其次，Geddes 法对于桩侧摩阻力分布模式的假设过于简单，不能很好地拟合实际长桩在工作荷载下的侧阻分布模式。长桩和超长桩的侧摩阻力常呈现多段式的分布规律：桩身侧摩阻力在一定范围内呈线性增长，超过一定深度后，侧摩阻力沿深度减小或基本保持不变。第三，该法忽略了群桩在土中的加筋与遮帘效应，其通过单桩计算成果进行简单叠加求得群桩产生的应力和位移，忽略了相邻桩的存在对单桩产生的影响，导致计算结果偏大。

由于Geddes 法存在上述问题，《建筑桩基技术规范》中提出了考虑桩径影响的Mindlin 解用于计算单桩、单排桩、疏桩的沉降。

考虑桩径影响，设桩端阻力沿桩端平面均匀分布，桩侧阻力分布于桩侧表面，分别为沿深度呈均匀分布和线性增长分布，据此分别计算桩端阻力、桩侧阻力对于地基中某一点的竖向应力系数。但是计算过程中只有当计算点位于桩轴线上时才能得到显式解，对于桩轴线以外的计算点由于得不到显式解，《建筑桩基技术规范》采用双重数值积分计算，并绘制了表格。

1.4 等效作用分层总和法

等代墩基法计算原理清晰、应用成熟，但是忽略了桩间土的压缩变形，最主要的缺点是竖向附加应力采用的是Boussinesq 解，计算土中应力偏大，从而导致其沉降计算结果不准确，而Geddes 法采用半无限体内荷载作用下的Mindlin 位移解，基于桩土位移协调条件，略去桩身弹性压缩，求解群桩的沉降数值解相对更准确，但是其计算更复杂。为实现既要计算简便、又使附加应力的计算更接近于实际的目标，《建筑桩基技术规范》对于桩中心距不大于6 倍桩径的群桩，其最终沉降量计算采用等效作用分层总和法。

等效作用分层总和法是在等代墩基法（不考虑应力沿桩基侧面的扩散）的结果上，乘以等效沉降系数ψe。等效沉降系数ψe是指依据相同的几何和变形参数，采用Mindlin 解与Boussinesq 解计算的沉降量之比，实质上纳入了Mindlin 解应力分布对计算沉降的影响。为应用方便，其结果采用数值回归参数表达式，按不同距径比、长径比、总桩数、不同布桩型式、桩基承台长宽比等列成参数表格，按照如下公式简化计算：

式中C0、C1、C2分别是与群桩距径比、长径比、承台尺寸有关的参数，nb为矩形基础短边布桩数。

等效作用分层总和法较为常用，但是也有一定的局限性。其计算基底仍位于桩端平面处，不考虑桩间土的压缩变形，但是引入了等效沉降系数后使结果更符合实际。桩端平面处的竖向附加应力取值与等代墩基法取值方法相同，仍取桩基承台底面的平均附加应力，比实际桩端附加应力偏大，桩越长应力误差越大，进一步导致压缩层厚度选取偏大、压缩模量取值偏大。

2 工程实例

2.1 工程概况

该新建水闸位于上海市崇明区老滧港与长江口交汇处，为3 孔节制闸，单孔净宽8m，闸底板顺水流方向长17m、垂直水流方向宽29.4m，厚1.5m，桩基础采用直径500mm 的PHC 管桩，桩长26m，桩间距2m，呈正方形布置，桩顶高程-1.5m，桩端高程-27.4m。闸室纵剖面图见图1。

图1 闸室纵横面图

2.2 地质条件

本工程拟建场地地貌单一，属河口、砂嘴、砂岛地基土类型。拟建场地现状为老水闸及管理区，且紧邻长江，地形有起伏，勘探期间所测孔口高程在3.21～8.85m 之间。场地地层见表1。

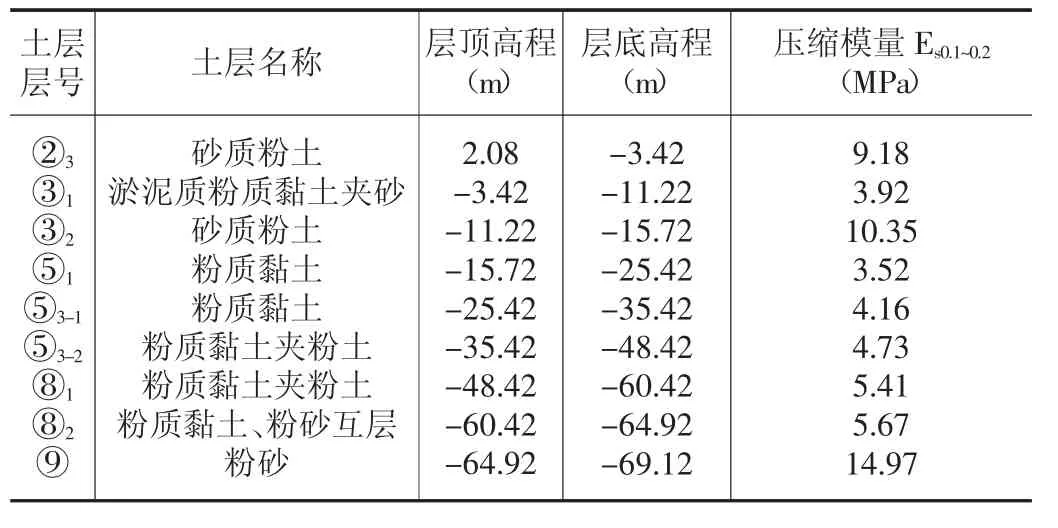
表1 场地地层性质

2.3 等代墩基法计算

依据《建筑地基基础设计规范》（GB50007-2011）的等代墩基法计算，采用桩端平面为计算基底，附加应力取承台底附加应力并沿桩侧按φ/4 扩散，桩长范围内的扩散角加权平均值为20.2°，扩散后桩端计算基底面积为630.9m2，桩端处附加应力为69.2kPa。计算结果见表2。

表2 等代墩基法计算表格

2.4 Geddes 法

依据《建筑地基基础设计规范》（GB50007-2011），采用不考虑桩径影响的Mindlin 课题的Geddes 法，假定桩侧摩阻力全部沿桩身线性增长（即三角形分布，β=0）。由于该法没有考虑桩径的影响，桩端处会产生应力集中，所以土体的计算分层厚度在桩端以下一定范围内进行适当加密，在桩端以下1m 内分层厚度取0.1m、1～10m 范围内取0.5m、10m 以下取1m。

附加应力取承台底部的附加应力89kPa，桩端阻力荷载分担系数α 取总端阻力极限值与单桩极限承载力之比0.159，则桩侧阻力荷载分担系数为0.841。分别计算各桩对底板中心计算点下不同深度的附加应力，计算得未经修正的沉降量为47.53mm，压缩模量的当量值为16.2MPa，桩基沉降计算经验系数为0.98，则最终计算沉降量为46.39mm。

2.5 等效作用分层总和法

依据《建筑桩基技术规范》（JGJ94-2008），对于群桩沉降计算采用等效作用分层总和法，等效作用面取桩端平面，附加应力取承台底平均附加应力，不考虑沿桩侧扩散，桩端附加应力为89kPa。计算结果见表3。

表3 等效作用分层总和法计算表格

2.6 与实测值对比分析

项目于2020 年12 月开工建设，2021 年7 月31 日闸室底板浇筑完成、11 月6 日闸室结构封顶。根据实测沉降结果，已基本完成固结沉降。

不同群桩沉降计算方法的结果与实测结果的对比结果见表4。

表4 不同计算方法对比表

等效作用分层总和法的计算基础是附加应力不沿桩侧扩散的等代墩基法，其桩端附加应力相较于地基规范中的等代墩基法更大，因此其未经修正前的计算沉降量更大。桩端以下土中应力两者都采用Boussinesq 解，因此两者计算的桩端以下土中应力都偏大，但是其引入等效沉降系数后，实质性地引入了Mindlin 解对沉降计算的影响，使得等效作用分层总和法的准确性明显提高。

Geddes 法是在Mindlin 解的基础上求解地基土中的应力，相对于Boussinesq 解，其是在半无限体内部作用的集中力引起的竖向应力，更符合桩基的特点，从表中数据可以看出，未经修正的沉降计算结果最接近实测值，计算准确性相对更高。但是规范中用于群桩沉降计算的Geddes 法并没有考虑桩径影响，使其桩端容易产生较大的应力集中，计算结果也偏大。规范中的修正系数偏大，本工程取值系数应为0.6。

3 结论

本工程通过上海市崇明区老滧港水闸的群桩沉降实例，结合实测沉降数据，验证了不同群桩沉降计算方法的准确性。由于群桩沉降影响因素多，目前各类方法均有一定的局限性，还需要通过工程积累提高计算成果的可靠性。

等代墩基法计算简单，应用广泛，为工程人员普遍接受，但是其采用Boussinesq 解导致其计算的土中附加应力偏大，计算误差较大，且无法考虑不均匀布桩、桩长不同等情况，难以应用于变刚度调平等设计方案中；Geddes 法是基于Mindlin 解计算土中附加应力，更合理，并且可以考虑桩基布置、不同桩长等情况，应用范围更广。其存在的问题一方面是计算相对更复杂，另一方面是不考虑桩径影响时桩端应力集中现象严重，且难以准确确定桩端阻力、桩侧阻力的分布型式及其荷载分担系数，不利于其推广应用；等效作用分层总和法集中了等代墩基法计算简便、Mindlin 解计算准确的优点，也带来了两者的缺点，比如不考虑桩间土的压缩、桩端附加应力偏大等。

目前各类规范采用的桩基沉降计算方法均为单向压缩分层总和法，采用各向同性均质变形体理论，与实际土体的性质不符，且没有考虑上部结构刚度的影响，仅能估算建筑物的最终平均沉降量，由于理论本身的局限，不建议用于建筑物下各点的不均匀沉降计算。