基于MATLAB 的永磁同步电机矢量控制系统的设计

李艳芳 LI Yan-fang

（西安工商学院，西安 710200）

0 引言

在特定领域中，永磁同步电机常常面临较为严苛的使用环境，这些环境要求高精度和很强的适应性。为了满足社会和生产生活的需求，我们需要结合先进的控制理论来不断升级和优化电机控制系统的性能。通过这种方式，我们可以确保电机性能的稳定性和精确性，从而在各种应用场景中表现出色。

在生产生活中，永磁同步电机广泛采用很多经典控制策略进行控制。在这些经典控制策略中，矢量控制方法因其高控制精度、小扭矩脉冲、优秀的调速性能和简易的异形结构，被认为具有卓越的控制性能。因此，矢量控制在电动机控制中得到了广泛应用。这种控制方法对科技进步和经济增长具有重要意义。

永磁同步电机控制性能的提升是我们持续优化的目标。借助计算机仿真实验，我们显著提升了设计效率，并对系统优化程度进行了精确量化。在处理复杂庞大的系统模型时，仿真方法展现出强大优势，既可直接进行实验，又能准确预测性能。对于无法进行实际试验的大规模电机系统设计，计算机仿真实验的价值尤为突出。

1 系统结构原理

永磁同步电机（PMSM）由两部分产生转矩：永磁转矩Te1 和磁阻转矩Te2。永磁转矩与定子电流转矩密切相关。PMSM 的转矩可以通过控制转矩分量来实现，而定子电流的分量则与电机的电枢电流相对应。此外，电机的磁场是由定子的励磁和磁链产生的，这与直流电动机的励磁电流相似。通过这种方式，实现了定子励磁和磁链的相互控制。

通过对加速器和控制器的加速计算，取得两个分量，分别是电流励磁转矩对应的id和iq信号。我们可以分别提取两个三相电流信号ia、ib。再将三相电流信号进行Clarke 变换，使其变换为α-β 的运动坐标系中，再将其通过Park 变换得到iq、id。

另一方面，再将d-q 坐标系的iq、id与它们的一个终点参考相对电流信号基准iq※、id※进行比较，控制器变换即可分别获得数值在旋转运动坐标系下的参考电压测量信号uq※、ud※，然后经过Park 变换，可以直接得到α-β 电压坐标系下的两个电压的信号uα※、uβ※，然后送入到SVPWM 中就可以会直接产生一个脉冲控制器的脉冲，通过这个脉冲控制器的脉冲，可以得到用来直接控制三相对称逆变器的各种开关启动时和开关正在运行时的状态，然后通过移除电流，可以直接控制当前三相电流。

从而就得到一个完整的电流速度双闭环控制系统，获得外环速度环产生的当前固定扭矩组件的参考值，电流环实际由信号控制。对控制策略进行分析与对比，再进行具体分析，使用id=0 的控制策略，因此控制当前电机电枢分量与电流励磁分量，其控制参考是一个输入id※=0。

以上分析了矢量控制的基本原理及策略，并且在这个基础上构建了转速电流双闭环的矢量控制框图。在构建好框图后，对其如何实现对转矩转速的控制进行了深入的分析。我们可以通过公式，发现转速和其他的分量之间存在的关系，进而分析永磁同步电机矢量控制的优缺点。

2 空间电压矢量调制（SVPWM）算法的实现

空间电压矢量调制（SVPWM）是一种新兴的控制策略，其核心目标是生成一个更为完美的椭圆磁链，主要由三相输入电压决定整体效果。相对传统的SPWM，SVPWM具有更大的基波分量，使得绕组中的电流波形谐波分量占比更小。这一特性有助于减小驱动电机的转矩和脉动系数，进而产生一个更接近椭圆的旋转磁场。此外，SVPWM还显著提高了直流母线对电压的综合利用率，使得电路的数字化更为简便。

接下来，我们将深入研究如何使用SVPWM 控制两级牵引逆变器。在永磁高频同步高速电动机的高速矢量运动控制模拟技术上，经过详尽分析后已基本实现。为了更好地完成模拟，采用了MATLAB/SIMULINK 矢量仿真工具模型以及永磁高速同步电机高速矢量运动控制各环节的矢量仿真工具模型，并对这些仿真模型进行了深入的剖析。

3 系统的仿真搭建

根据永磁同步电机的向量控制系统框架，主要任务是使用Matlab 仿真工具来构建该系统的仿真模型。为了完成这一任务，采用了模块化控制理念，将整个系统划分为一系列独立且功能独立的子模块。遵循从局部到整体的构建原则，逐一完成了这些子模块的搭建工作。通过优化整合这些子模块，我们成功地在Matlab/Simulink 中创建了永磁同步电机矢量控制系统的仿真模型。

借助Simulink 模块库中的PMSM 模型、开关元件、智能单元模块、测量设备和采样设备等工具，我们成功地简化了实际操作中的难度和复杂性。经过仔细的比较和选择，我们只需设计以下几个关键模块：坐标系转换模块、速度控制环、电流控制环和SVPWM 模块。

3.1 系统各仿真模块的搭建

在仿真永磁同步电机的矢量控制系统时，重点关注电流PI 控制器的电流调节，以及从电流转换到d-q 坐标系的分量id和iq。在进入SVPWM 模块之前，这些电流分量经过转换，成为a-β 坐标系中的iα和iβ。这一转变得益于Park 逆变换的运用。经过调节，永磁同步电机的三相输出完全符合要求。然而，为了实现系统反馈控制，需要明确iα和iβ的电流分量，这要借助坐标系的转换。首先，通过Clark 变换，将它们转换为iα和iβ的反馈量，随后再通过Park 变换，将其转化为控制系统所需的id和iq反馈模式。

3.2 Park 逆变换

Park 逆变换又叫直交变换，由d-q 轴的直流量，最终变换到αβ 的交流量，图1 表示Park 逆变换的仿真模块。

图1 Park 逆变换

3.3 Park 变换

Park 变换的本质是静止坐标系αβ 乘以一个旋转矩阵，从而得到d-q 坐标系，图2 表示Park 逆变换的仿真模块。

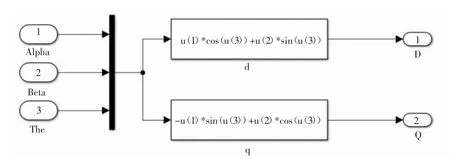
图2 Park 变换

3.4 Clack 变换

将ABC 的定子静止坐标系的各物理量变换到2 轴的定子静止坐标系中。该过程称为Clack 变换。图3 表示Park 逆变换的仿真模块。

图3 Clack 变换

3.5 仿真实验参数设定

电机参数如表1 所示。

表1 电机参数

3.6 仿真实验的分析

给定转速1000rad/min 时，三相定子电流所对应的波形如图4 所示。

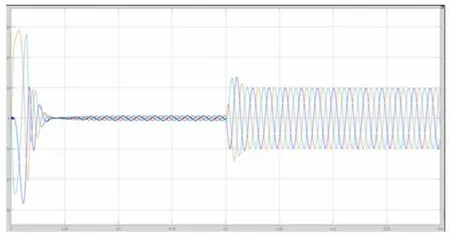
图4 三相定子电流波形

给定转速1000rad/min 时，转矩曲线所对应的波形如图5 所示。

图5 转矩曲线

给定转速1000rad/min 时，实际测量转速所对应的波形如图6 所示。

图6 给定转速1000rad/min 转速曲线

给定转速200rad/min 时，实际测量转速所对应的波形如图7 所示。

图7 给定转速200rad/min 转速曲线

给定转速1000rad/min 时，单相定子电流所对应的波形如图8 所示。

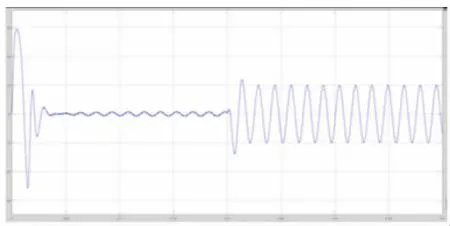
图8 单相定子电流波形

4 结论

本文为了实时观察转矩驱动器和发电机的各个输出量以及跟着转矩的驱动指令的数值发生改变时所产生的动、静态转矩响应，从这个过程仿真的实验结果来看，在一台动力电机全部成功通电后，转矩迅速地达到了最大转矩，然后在很长一段时间内恢复至一个稳定的转矩值并且继续保持恒定。

通过转速分析仿真对比系统给定1000rad/min 和200rad/min 的参考仿真转速结果，可以明显发现，系统给定的参考转速200rad/min 已经完全达到了稳定的系统运行速度状态。从参考仿真转速结果可以清楚地看出，在给定1000rad/min 的高速参考仿真转速下，系统的转速响应非常迅速，并且能够迅速且完全达到稳定的运行状态。为了进行比较，我们还对系统给定200rad/min 的参考仿真转速进行了分析。通过对比这两个转速的仿真结果，我们可以观察到系统在不同转速下的性能表现，可以发现，系统给定的参考转速200rad/min 已经完全达到了稳定的系统运行速度状态。