基于Dijkstra 算法的搬运车省时路径规划研究

闫恩雪 YAN En-xue；张石强 ZHANG Shi-qiang

（河北工程大学，邯郸 056038）

0 引言

随着现代工业技术的不断提高，越多越多的企业车间使用智能搬运车，智能搬运车在很多领域都得到了认可，目前国内外都在扩展使用智能搬运车。智能搬运车一般多用于制造业、物流仓储等行业，代替人工进行高体力劳动，随着国家对工业化、智能化的重视，智能搬运车行业逐渐壮大起来。在多数发达国家，智能搬运车的应用更为广泛，自引进智能搬运车后，不仅车间的安全性提高，而且工作效率也大大提高，如今智能搬运车正在向更多行业进行迈进。

智能搬运车被使用和认可的同时，如何更高效的利用智能搬运车成为了大家的关注点。智能搬运车的高效使用与其行驶路径息息相关，一条好的行驶路径不仅路程最短，还要行驶时间更节省，这样以来既省电又省时，大大提高工作效率。路径规划是当今的一个研究重点，经典的路径规划算法有：Dijkstra 算法、蚁群算法、遗传算法、A*算法等。在这些路径规划算法中，仅有Dijkstra 算法能够稳定地实现全局最优路径的搜索，而其它算法都有可能因为陷入局部最优而搜索出次优路径，因此本文选择Dijkstra算法进行研究，对Dijkstra 算法进行改进，保留既短又省时的路径，提高工作效率，降低工作成本。

1 Dijkstra 算法概述

1.1 Dijkstra 算法介绍

Dijkstra 算法是当今最短路径的经典算法之一，是荷兰计算机科学家狄克斯特拉在1959 年提出的“贪心算法”模式，是解决有权图的最短路径问题的方法。按照路径递增次序产生算法，算法复杂度为n2，通过以某个顶点作为起点向其他所有点扩展，把他们之间的距离保存下来，再筛选出各两点之间的最短距离，作为最终的最短路径。Dijkstra 算法具有适用广、不存在负权边的特点，有效计算有向图的最短路径问题。

Dijkstra 算法具体步骤如下：

步骤一：初始化。初始集合S 中只有S0点，剩余节点都在U 集合，从S0向各点延伸，与S0相邻的点之间的距离为s，标记为临时标号T=s，与S0不相邻的点，标记为T=+∞。

步骤二：在集合U 中，同一节点经对比所有T 标号中选择最小值标记为永久标号P，此时P 标号的来源即为一条最短路径。

步骤三：将P 标号从U 集合转移到S 集合。

步骤四：重复步骤二和步骤三，至所有节点都转移到S 集合时运算结束。

1.2 改进Dijkstra 算法

传统Dijkstra 算法最终只保留一条最短路径，而在计算的过程中可能会出现多个最优解，就有可能出现被筛除掉的路线是最多因素影响下最佳的路线。本文对Dijkstra算法进行改进，在路线规划时，将所有搜索到的最短节点不进行选择，都保留下来。再从这些节点搜索所用时间最短的路径，改进算法是考虑了相同路程长度时，由于拐弯时减速-拐弯-加速的过程导致的时间不同，改进单纯的最短路径，得到高效低成本的方案。

改进Dijkstra 算法具体步骤如下：

步骤一：初始化。设置初始集合S 与其余节点集合U，找到与S0点相邻距离最短的节点Si，将Si节点从集合U转移到集合S。其余集合U 中与S0不相邻的点，标记为T=+∞。

步骤二：从Si出发，在集合U 中寻找相邻节点Sj，同一节点经对比所有T 标号中选择最小值标记为永久标号P，同时将Si节点放入前驱节点集合B 中，此时保留P 标号的来源即为一条最短路径，放入最短路径集合C 中。

步骤三：将P 标号从U 集合转移到S 集合。

步骤四：重复步骤二和步骤三，至U 集合变为空集时，将保留的不唯一的最短路径分别计算其运行时间。

步骤五：对最短路径集合C 进行时间计算，并筛选保留运作耗时最少的路径为最优路径，计算结束。具体步骤如图1。

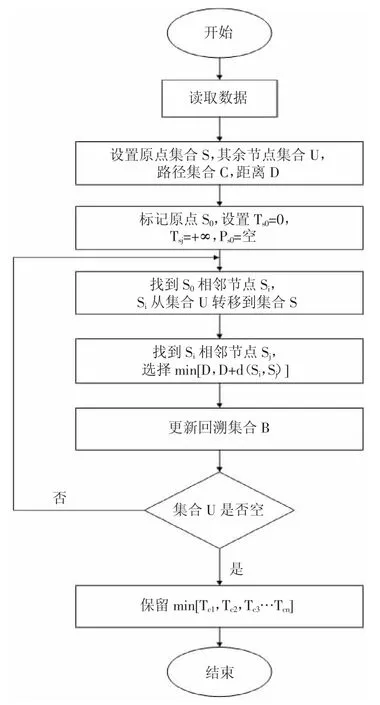
图1 改进Dijkstra 算法流程图

2 E 公司生产车间省时路径规划案例分析

E 公司是一家微波炉制造商，其生产车间采用柔性生产线，由于产品的组成重量大、体积大、易磕碰，为了在生产过程中搬运更方便安全，生产车间引进了智能搬运车。现为了使智能搬运车运行效率更高，将对E 公司生产车间的智能搬运车的行驶路线进行更新。

2.1 电子地图建模

地图建模通常有三种：栅格图法、可视图法、拓扑结构图法。本文的案例E 公司生产车间布局规整，搬运车行驶路程简单，车间内工作台、货物存放等清晰明了，可以看作为矩形。因此栅格图法更适合E 公司生产车间的环境地图建模。

根据E 公司生产车间的实地情况，采用16×16 的栅格计算结果会更精准，将生产车间智能搬运车可行驶的区域用白色表示；将操作台、货物、流水线看做障碍物，用黑色表示。

可行驶区域用0 代表，障碍物区域用1 代表，在MATLAB 中运用公式F={0，1}

输入每个格子的属性；用坐标（x，y）表示每个格子的位置，左下角为（1，1），右上角为（16，16），来表示16×16 的栅格图。其中右下角为生产车间的入口，根据E 公司生产车间的情况，建模地图如图2 所示。

图2 E 公司生产车间栅格图法电子地图

2.2 建立省时路径规划模型

根据E 公司生产车间实地情况，现对生产车间进行路径规划建模前，先进行相关条件假设与相关参数设置。以下求解计算基于该数据进行。

相关条件假设：

①智能搬运车拐弯时是直角原地拐弯，拐弯半径看作为0。

②智能搬运车拐弯时先减速到拐弯速度，进行拐弯，再加速为直线匀速行驶的速度。

③不考虑货物的重量对搬运车的速度影响。

④智能搬运车一趟只送一种货物，完成该任务后再进行下一项任务。

E 公司生产车间智能搬运车的相关参数设置如表1。

表1 智能搬运车相关参数设定

本文在计算最短路径的基础上多加了该路径对应的时间计算，更详细的解释了选择该路径的优点。将一条路径的总时间分为减速运动总时间、加速运动总时间、匀速运动总时间这三个部分计算。

减速运动总时间Ta1：

加速运动总时间Ta2：

其中，减速运动行驶的路程为：

加速运动行驶的路程为：

匀速直线所行驶的路程Lv1：

匀速直线运动总时间Tv1：

将减速运动总时间、加速运动总时间、匀速运动总时间相加的到一条路径的总时间Ttotal：

约束条件为：

优化目标为：

上述公式中i 为需要减速拐弯的节点，j 为拐弯后需要加速的节点，L原始为原来的智能搬运车的行驶路径的长短，T原始为原来的智能搬运车行驶路径所需的时间，使用MATLAB 进行路径及时间的建模，经过计算比较得出更省时、低成本、高效的路径。

2.3 改进算法流程的实施

求解过程使用到MATLAB，将改进的Dijkstra 算法代码输入进行运行求解，得到最终路径最短中的最省时路径。具体步骤如下：

①调查E 公司生产车间的实地情况，设计黑白两色栅格图，黑色代表障碍物，白色代表可通行。

②读取数据，设置初始集合S 与其余节点集合U，找到与起始点S0点相邻距离最短的节点Si，将Si节点从集合U 转移到集合S。

③从Si出发，在集合U 中寻找相邻节点Sj，同时将Si节点放入前驱节点集合B 中，此时保留P 标号的来源即为一条最短路径，放入最短路径集合C 中。将P 标号从U集合转移到S 集合。

④重复③，至U 集合变为空集时，保留所有最短路径。

⑤对最短路径集合C 进行时间计算，并筛选保留运作耗时最少的路径来源为最优路径，计算结束，输出结果。（图3）

图3 改进Dijkstra 算法的重点部分

3 搬运车路径优化前后对比

根据图2，将E 公司生产车间看作为256 个小方格，E公司生产车间共有5 项智能搬运车的运输任务，5 项任务分 别 为：（5，3）→（14，11）；（14，11）→（3，15）；（3，15）→（14，14）；（14，14）→（6，5）；（6，5）→（14，6），结合智能搬运车的相关参数，不受其他因素的影响，经过计算优化前后智能搬运车的路径具体信息如表2 所示。

表2 搬运车路径优化前后对比

优化前后对比可以看出，路程长度相等的情况下，也可能出现耗时不同，由于加速减速的过程可能会耗费不必要的时间，因此本次路径优化可以有效减少智能运输车的行驶时间，节省时间可以提高效率。任务一，在优化前路程长为17 米，所耗时间为19.78 秒，优化后路程长为17 米，所耗时间为18.6 秒，节省了1.18 秒；任务二，在优化前路程长为15 米，所耗时间为23 秒，优化后路程长为15 米，所耗时间为17.4 秒，节省了5.6 秒；任务三，在优化前路程长为12 米，所耗时间为14.6 秒，优化后路程长为12 米，所耗时间为13.8 秒，节省了0.8 秒；任务四，在优化前路程长为17 米，所耗时间为19.6 秒，优化后路程长为17 米，所耗时间为18.6 秒，节省了1 秒；任务五，在优化前路程长为13 米，所耗时间为15.4 秒，优化后路程长为9 米，所耗时间为10.8 秒，节省了4.6 秒。优化后的路径在长度的时间上优于优化前的，选择优化后的将更有利于E 公司生产车间的发展。

4 结语

当今制造业发展蓬勃，智能搬运车的使用也在快速普及。工作效率受到多重因素影响，只考虑路程长短已经不能被满足，路径规划中可以选择路程和时间双因素，全面计算更高效的路径方案，为企业实现降本增效。

本文基于改进Dijkstra 算法对E 公司生产车间的智能搬运车的路径进行重新规划，先是对Dijkstra 算法的后续加上了不进行筛选，保留所有最短路径，再对保留的所有路径进行时间计算。由于智能搬运车在行驶的过程中遇到拐弯时会出现变速的情况，进而影响到整体的运行时间，通过将保留的最短路径进行时间计算，可以有效的筛选出既路程短，又耗时少的路径，节省下来的时间可以做更多的工作，以提高整体的工作效率。通过E 公司生产车间的智能搬运车的五个任务线案例，数据清晰的表明了该Dijkstra 改进方法可以实现省时省力的目标，在未来可为企业带来更大的利润。