基于GPU加速的等几何拓扑优化高效多重网格求解方法

杨峰 罗世杰 杨江鸿 王英俊

摘要：

针对大规模等几何拓扑优化（ITO）计算量巨大、传统求解方法效率低的问题，提出了一种基于样条h细化的高效多重网格方程求解方法。该方法利用h细化插值得到粗细网格之间的权重信息，然后构造多重网格方法的插值矩阵，获得更准确的粗细网格映射信息，从而提高求解速度。此外，对多重网格求解过程进行分析，构建其高效GPU并行算法。数值算例表明，所提出的求解方法与线性插值的多重网格共轭梯度法、代数多重网格共轭梯度法和预处理共轭梯度法相比分别取得了最高1.47、11.12和17.02的加速比。GPU并行求解相对于CPU串行求解的加速比高达33.86，显著提高了大规模线性方程组的求解效率。

关键词：等几何拓扑优化；方程组求解；h细化；多重网格法；GPU并行计算

中图分类号：TH122

DOI：10.3969/j.issn.1004132X.2024.04.004

开放科学（资源服务）标识码（OSID）：

A GPU-accelerated High-efficient Multi-grid Algorithm for ITO

YANG Feng1  LUO Shijie1  YANG Jianghong1  WANG Yingjun1，2

1.National Engineering Research Center of Novel Equipment for Polymer Processing，School of

Mechanical and Automotive Engineering，South China University of Technology，Guangzhou，510641

2.State Key Laboratory of Digital Manufacturing Equipment and Technology，Huazhong University

of Science and Technology，Wuhan，430074

Abstract： An efficient multi-grid equation solving method was proposed based on the h-refinement of splines to address the challenges posed by large-scale ITO computation and low efficiency of traditional solving methods. By the proposed method， the weight information obtained through h-refinement interpolation between coarse and fine grids was used to construct the interpolation matrix of the multi-grid method， thereby enhancing the accuracy of mapping information for both coarse and fine grids and improving computational efficiency. Additionally， a comprehensive analysis of the multi-grid solving process was conducted， culminating in the development of an efficient GPU parallel algorithm. Numerical examples illustrate that the proposed method outperforms existing methods， demonstrating speedup ratios of 1.47， 11.12， and 17.02 in comparison to the linear interpolation multi-grid conjugate gradient method algebraic multi-grid conjugate gradient method， and pre-processing conjugate gradient method respectively. Furthermore， the acceleration rate of GPU parallel solution surpasses that of CPU serial solution by 33.86 times， which significantly enhances the efficiency of solving large-scale linear equations.

Key words： isogeometric topology optimization（ITO）; system of equations; h-refinement; multi-grid method; GPU parallel computing

收稿日期：20230813

基金項目：国家自然科学基金（52075184）；数字制造装备与技术国家重点实验室开放基金（DMETKF2021020）

0  引言

拓扑优化是一种根据给定载荷、约束条件及性能指标，对设计区域内材料按照优化准则自动分布，从而获得高性能结构的方法，具有较高的设计自由度，是近些年结构设计、增材制造等领域的研究热点［1］。目前常见的拓扑优化方法有变密度法［2］、均匀化方法［3］、水平集法［4］、渐进结构优化法［5］、移动变形组件法［6］等，这些方法已被广泛应用于航空航天［7］、船舶汽车［8］、医疗器械［9］、桥梁建筑［10］等领域，具有重要的工程价值。

传统拓扑优化的结构性能分析采用有限元法，其形函数单元间的C0连续在高阶问题上难以满足求解精度，而且在设计分析优化过程中，CAD数据与CAE数据表达方式不一致将导致模型转换繁琐，并导致优化结构模型的边界曲线轮廓无法精确表达［11］。为了解决求解精度和连续性的要求，HUGHES等［12］采用CAD系统中的B样条或非均匀有理B样条（non-uniform rational basis spline， NURBS）基函数替代拉格朗日插值函数作为离散物理场的形函数，实现了CAD模型和CAE模型的统一表达，避免了模型数据转化，并且提高了单元间连续性。

基于GPU加速的等几何拓扑优化高效多重网格求解方法——杨  峰  罗世杰  杨江鸿等

中国机械工程 第35卷 第4期 2024年4月

近年来，等几何拓扑优化（isogeometric topology optimization，ITO）得到了广泛的研究与发展。SEO等［13］基于等几何方法提出了一种新型拓扑优化方法（即ITO），为结构设计、分析、优化的一体化研究奠定了基础。KUMAR等［14］将等几何分析（isogeometric analysis， IGA）和变密度拓扑优化集成，得到了基于控制点密度的ITO方法。GAO等［15］公开了一套高效、紧凑的ITO的MATLAB代码，便于更多学者开展研究。关于ITO的介绍详见WANG等［16］和GAO等［17］的综述。目前，ITO已广泛应用于各种工程实际问题的优化，如对梁结构的优化［18］、振动膜的形状优化［19］、流体的优化［20］等。

ITO中每次迭代都需要对IGA方程进行求解［21］，该部分占据了ITO主要时间成本［22］，并且相比有限元分析，IGA刚度矩阵方程系数更加稠密，计算量更大。因此，研究IGA方程的高效求解方法是提高ITO计算效率的重要途径。多重网格（multigrid， MG）法是求解偏微分方程数值解的有效方法之一，具有收敛性能好、求解速度快的优势，通常用作黑箱求解器或者预处理共轭梯度法（preconditioning conjugate gradient， PCG）的预处理器［23］，被广泛应用于大规模线性方程组的求解。刘石等［24］通过将IGA与多重网格共轭梯度法（multigrid conjugate gradient method， MGCG）结合，用于计算泊松方程，结果表明MGCG比MG法的收敛速度更快。WANG等［25］通过将多级网格、多重网格共轭梯度法和局部更新策略三者相结合，实现了ITO的三重加速，计算时间与传统ITO相比减少了37%～93%，且优化结果保持一致。

在ITO中，即便使用了高效线性方程组求解方法MGCG，串行程序的计算成本仍很高，故必须寻求更高效率的解决方案。GPU并行计算是一种高效且经济的加速方法，仅依赖普通显卡即可实现数十倍甚至上百倍的加速比。因此，众多学者采用GPU并行计算对线性方程组求解以及拓扑优化流程进行加速。邓亮等［26］将GPU并行计算应用到流体力学偏微分方程的求解中，相对于串行算法实现了17倍左右的加速比。XIA等［27］将GPU并行和ITO结合，速度相比串行程序提升了两个数量级。韩琪等［28］对双向渐进结构拓扑优化算法进行改进，实现了大规模迭代算法的并行计算，验证了并行计算方法的稳定性和高效性。

在ITO中，采用线性插值的多重网格共轭梯度法（linear interpolation MGCG， L_MGCG）的效果较好，但该方法存在数值不稳定的现象，该现象可能是线性插值关系不能精确表达ITO中样条粗细网格的映射信息所导致的。基于上述研究，本文提出一种基于h细化插值网格的多重网格共轭梯度法（h-refinement interpolation MGCG， h_MGCG），在ITO中，该方法的插值关系相比L_MGCG更加准确，能更高效地完成方程求解。同时结合GPU并行计算，从硬件和算法两个方面提高加速比，显著提高了求解效率。最后，通过二维与三维的数值算例验证了所提方法在ITO中具有适用性强、迭代收敛速度快、求解效率高以及稳定性能好的优点，并证明了基于GPU并行计算的求解方法与单CPU计算的求解方法具有相同的计算精度。

1  理论基础

1.1  NURBS基函数

IGA将NURBS基函数作为单元的形函数，从而实现CAD建模和CAE分析的统一表达。B样条曲线是在Beziers曲线的基础上提出的更为灵活的建模方式，它在精确表达模型的同时还能随意增加控制点个数，从而进行局部修改。NURBS在B样条的基础上加入了权重系数，使其能够准确表示二次规则曲线曲面，在ITO中获得广泛应用。NURBS包括节点矢量、控制点向量和权重等要素，其节点矢量可以是非均匀的，即相邻節点间的距离可以不相等，可记为Ξ=（ξ1，ξ2，…，ξn+P+1），其中，ξi为第i个节点，P是基函数的阶次，n是基函数和控制点的个数。B样条的基函数由Cox-deBoor递推公式定义为

P=0时：

Ni，0（ξ）=1  ξi≤ξ≤ξi+1

0其他（1）

P≥1时：

Ni，P（ξ）=ξ－ξiξi+P－ξiNi，P－1（ξ）+

ξi+P+1－ξξi+P+1－ξi+1Ni+1，P－1（ξ） （2）

引入权重系数wi，j，得到二维NURBS基函数表达式：

R（P，Q）i，j（ξ，η）=Ni，P（ξ）Ni，P（η）wi，j∑ni=1∑nj=1Ni，P（ξ）Nj，Q（η）wi，j（3）

式中，Ni，P、Nj，P分别为两个参数方向对应的B样条基函数；P、Q分别为沿曲面两个参数方向的基函数阶次。

1.2  基于控制点密度的ITO

在基于密度法的ITO中，采用的材料插值方法为固体各向同性材料惩罚法（solid isotropic material with penalization，SIMP），每个单元将被赋予取值范围在0～1之间的相对单元密度，而其单元e（e=1，2，…，n）的密度xe和弹性模量Ee之间的关系为

Ee（xe）=Emin+xpe（E0－Emin）  xe∈［0，1］（4）

式中，Emin为弹性模量最小值（Emin>0），其作用为防止刚度矩阵发生奇异；E0为相对单元密度为1的实心单元的弹性模量；p为惩罚系数，通常取3。

经典的以柔度为目标、以体积为约束的拓扑优化问题可表示为

find x=（x1，x2，…，xn）T

min C（x）=UTKU=∑Ne=1Ee（xe）uTekeue

s.t.KU=F

V（x）/V0≤VF

0≤xe≤1（5）

式中，C（x）为目标函数，表示结构柔度值；x为设计变量；N为设计域中设计变量的个数；U为总体位移向量；F为施加载荷向量；K为总体刚度矩阵；ue为单元e的位移向量；ke为单元e的单元刚度矩阵；V0为最初设计域总体积；VF为体积比约束（VF∈［0，1］）。

在IGA中，单元刚度矩阵ke计算公式如下：

ke=∫Ω^eSTDS|J1|d=∫eSTDS|J1||J2|d（6）

式中，S为应变位移矩阵；D为弹性矩阵；、分别为NURBS参数空间Ξ（m）和高斯积分参数域（m）对应的参数空间；J1、J2分别为从NURBS参数空间转换到物理空间和从高斯积分域转换到NURBS参数空间的雅可比矩阵。

与传统的基于单元密度的SIMP法不同，基于控制点密度的ITO可将设计变量作为控制点网格中的高一维坐标。ITO中参数坐标为ξ的点的密度x可由附近控制点的密度求出：

x（ξ）=∑iNi（ξ）xi（7）

式中，Ni为第i个控制点的NURBS基函数；xi为控制点密度，本文以单元中心点的密度作为该单元的密度。

目标函数C对xe的偏导数由下式求得：

Cxe=－p（xe）p-1（E0－Emin）uTekeue（8）

因此，在ITO中计算灵敏度的公式由传统SIMP法求解灵敏度公式改写成

Cxi=∑j∈eiCxeijxeijxi=

∑j∈ei－p（xeij）p-1uTeijkeijueijxeijxi（9）

式中，ei为控制点i影响的所有单元；eij为ei中的第j个单元。

1.3  基于h细化的多层网格策略

在ITO的实际应用中，精确表示物理模型需要使用精细网格。ITO通常采用h细化、p细化和k细化等方法进行细分，这些方法都可以保持原始形状不变。本文采用h细化，即将多个节点插入NURBS曲线而不改变其阶次，该过程只改变向量空间的基底，而曲线的几何形状和参数化保持不变。在h细化中，插入节点∈［ξk，ξk+1］到节点向量T=（ξ0，ξ1，…，ξn+k+1）可得到新的节点向量

=（0=ξ0，…，k=ξk，k+1=，k+2=ξk+1，…，n+k+2=ξn+k+1），然后得到新樣条控制点对应的坐标计算公式：

Qnewi=αiQoldi+（1－αi）Qoldi－1（10）

其中，Qnew为新控制点的齐次坐标；Qold为旧控制点的齐次坐标；αi由下式得到：

αi=1      i≤k－p

－ξiξi+p－ξik－p+1≤i≤k

0i≥k+1（11）

因此，h细化在数学上可表示为矩阵运算：Qnew=P·Qold，P为将旧控制点序列映射到新控制点序列的投影系数矩阵。而细网格到粗网格的限制矩阵求解比较困难，本文直接取投影系数矩阵的转置R=PT。二维的情况同理，只需在u、v两个方向分别进行h细化得到映射矩阵Pu、Pv，从旧控制点到新控制点的投影系数矩阵为

Puv=Pu·Pv（12）

以图1为例，细化前节点向量为（0，0，0，0.5，1，1，1）×（0，0，0，1，1，1），在u、v方向进行h细化，细化后向量为（0，0，0，0.25，0.5，0.75，1，1，1）×（0，0，0，0.5，1，1，1），细化前后各参数方向的NURBS基函数如图1所示。

2  h_MGCG及其并行算法实现

2.1  基于h细化的MGCG

多重网格方法主要包括几何多重网格

（geometric multigrid， GMG）和代数多重网格（algebraic geometric multigrid， AMG）两类，AMG不依赖实际网格信息与几何模型，完全根据矩阵的代数信息求得各层级的系数矩阵，GMG依赖几何信息得到一系列不同规模的矩阵。但是两者求解的流程基本相同，都可分为前处理阶段和求解阶段。前处理阶段生成多层级矩阵以便于后续的求解；求解阶段由共轭梯度（conjugate gradient， CG）和多重网格（MG）两部分组成，通过反复迭代来获得满足条件的最终结果。具体过程包括将网格进行粗化，在细网格上先进行迭代以消除高频残差分量，然后将难以消除的低频分量映射到粗网格，使其变成相对高频分量，并在粗网格上进行求解以消除相对高频分量，最后将结果返回到细网格，循环反复前述过程直至达到设定的精度要求。

本文中，位移向量为U，载荷施加向量为F，刚度矩阵为K，对应不同层级的向量和矩阵分别表示为Ul、Fl、Kl，多重网格中的插值矩阵Pl即为前文所述h细化中新旧控制点的映射关系，限制矩阵用Rl=PTl代替，粗化矩阵Kl+1可以通过Galerkin投影方法［29］计算得到：

Kl+1=RlKlPl（13）

MG求解阶段可以分为前光滑处理、计算残差、限制投影、粗矩阵直接求解、插值校正、后光滑处理这6个步骤，MG算法具体求解流程见表1。

前后光滑处理的目的是减小求解中的振荡误差，通常采用Jacobi、Gauss-Seidel和SOR平滑处理。本文的光滑处理采用带权重的Jacobi矩阵：

Ul=Ul+wD-1l（Fl-KlUl）（14）

式中，Dl为矩阵Kl的对角矩阵；w为权重系数，具体细节可参考文献［30］。

预处理共振梯度（PCG）方法收敛速度快，但需要良好的预条件，而MG本身就是一种有效的预条件。将MG与PCG相结合，通过调用MG_Solve求解一次Kzi=ri方程取得的近似解代替PCG中的zi=M-1ri。MGCG算法流程见表2。

如前文所述，h_MGCG与其他MGCG方法的主要区别在于插值矩阵和限制矩阵的获取方式不同，其他实现步骤相同。在h细化过程中，尽管提取插值矩阵P需要通过样条插值完成，但是在整个拓扑优化过程中P保持不变，故只需在拓扑优化前处理阶段执行一次提取操作。相比之下，在AMG中每次进行拓扑优化迭代得到新刚度矩阵K后都要重新提取代数网格信息。因此，h_MGCG求解方法能减少拓扑优化过程中MGCG前处理阶段的总时间。

2.2  h_MGCG并行计算流程

由2.1所述理论基础，h_MGCG求解过程中CG迭代和MG部分求解阶段，主要进行的是易于并行的矩阵运算，故该部分可采用GPU进行并行计算。而在MG部分的前处理阶段，主要工作是通过h细化得到插值矩阵P，该阶段只需进行一次且花费时间很少，所以不采用GPU并行计算。本文为了提高粗矩阵部分的求解效率，采用cholesky分解进行直接求解，该求解算法为串行算法，且粗矩阵规模较小，GPU与CPU之间的通信开销很小，故该部分为CPU串行计算。最后再将结果返回到GPU，进行后续插值修正和后光滑处理。h_MGCG并行求解方法（GPU_h_MGCG）以及整个ITO中的流程如图2所示。

2.3  并行计算关键核函数

结合MGCG算法流程及图2所示的流程图，在h_MGCG求解线性方程组KU=F的过程中，耗时较多的部分有向量的加减运算、标量与向量的乘法运算、矩阵与向量的乘法运算、向量的点积运算，在CPU串行求解方法中这些运算占用大部分时间。针对这些耗时较多的求解过程，利用CUDA架构将其在GPU上实现并行化。向量的加减运算、标量与向量的乘法运算根据向量元素个数n分配线程块（block）数量num_blocks，将每个Block中线程（thread）数目num_threads取512，则num_blocks可通过下式求得：

num_blocks=（n+num_threads-1）/num_threads

其中，第id个线程将X、Y向量的第id个元素分别和常数a、b相乘并相加，将结果存在Z向量中，伪代码如下：

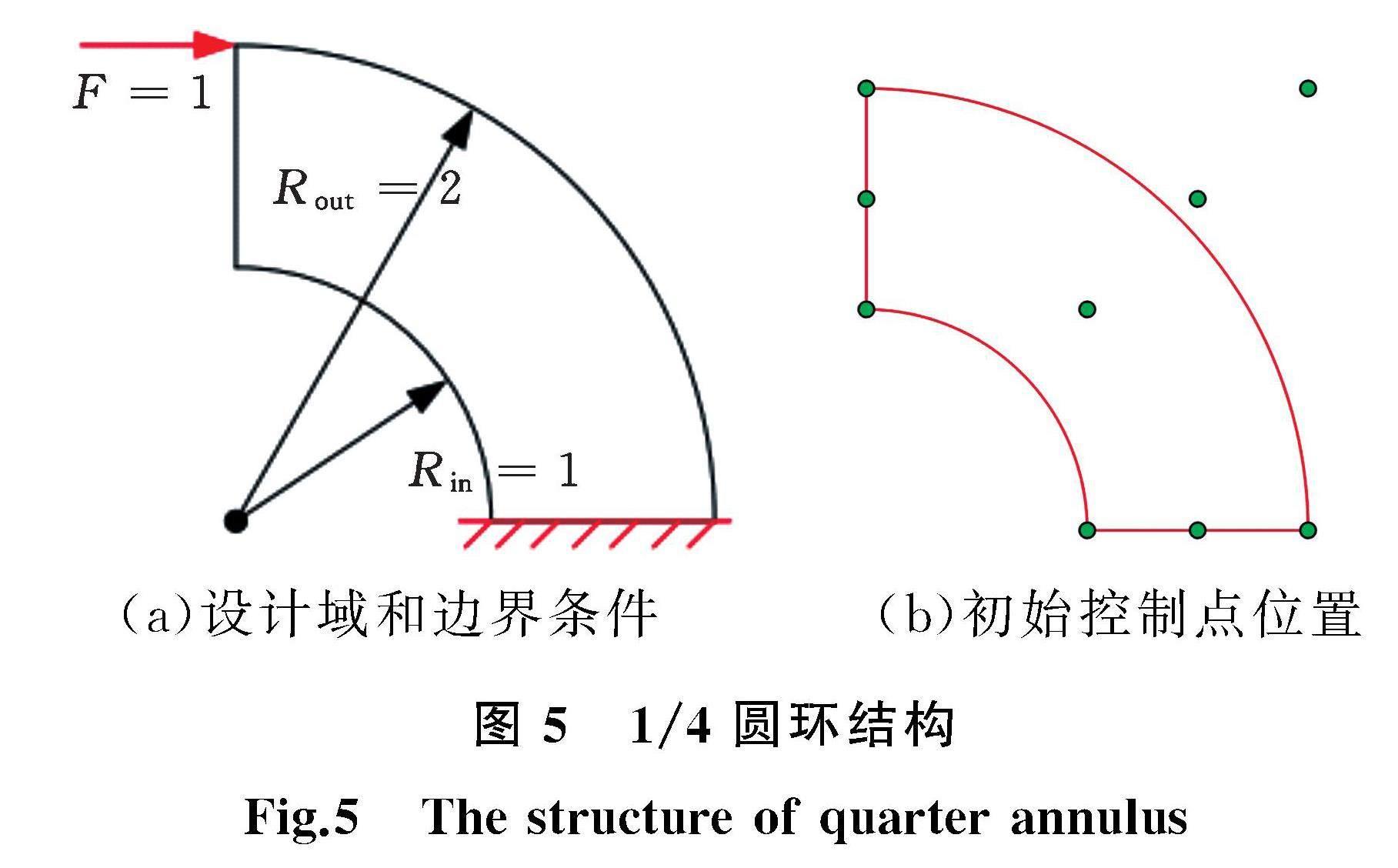
if（id

Z［id］=aX［id］+bY［id］;

end

在MG中前后光滑处理的带权重的Jacobi迭代法的迭代式即为式（14），

其中涉及矩阵求逆，由于该Dl矩阵为对角阵，故对其求逆只需取对角线元素的倒数即可，其线程分配同上，伪代码如下：

if（id

d［id］［id］=1/D［id］［id］;

end

矩阵与向量的乘法运算实现难度相对较高，也是GPU_h_MGCG并行求解方法中最耗时的部分。为了节省空间和提高运算效率，该求解方法使用了压缩行存储（compressed sparse row， CSR）格式，IK、JK、val分别表示矩阵非零元素的行偏移量、列索引和值，例如矩阵K的存储：

K=1700028050800604

IK=［0  2  4  6  8］

JK=［0  1  1  2  0  2  1  3］

val=［1  7  2  8  5  8  6  4］

矩阵K与向量X的乘法运算的一种简单实现方式如下：在GPU中分配n个线程，其中第id个线程负责矩阵K中第id行与向量X相乘，并将结果储存为向量Y的第id的元素。该方法的伪代码如下：

if（id

for（i=IK［id］; i

Y［id］+=val［i］X［i］;

end

end

但是这种分配方式的缺点是同一线程束（warp）中相邻线程不能访问相邻地址，因而内存访问效率低下。为了提高内存访问效率，同时减少线程资源闲置，本文的并行方案采用LightSpMV（light sparse matrix vector multiplication）方法［31］，该方法线程块和线程调整更合理，从稀疏矩阵平均每行非零元素数量动态分配线程束子块来求解，通过线程束shuffle指令实现同一线程束的线程交互，减小访存的延迟（latency）。因为直接访问寄存器比从共享内存（shared memory）中取值的延迟更低，因此LightSpMV方法实现了内存合并访问，避免了线程资源的浪费，大幅提高并行求解效率，其线程块及线程的分配、核函数的并行策略等具体细节可参考文献［31-32］。

向量的点积运算的速率也是影响求解时间的关键因素，其步骤包括将两个向量的对应元素相乘并将相乘的结果进行累加求和。由于最终结果依赖于每个线程求得的结果，故需要进行归约求和。其核函数步骤比较复杂，包括申请共享内存空间、向量运算及同步操作。具体流程如下：①每个GPU线程负责两对元素的相乘并求和，同时对线程块内进行同步操作，保证向量运算结束时将所得的值存在共享内存之中；②将每个线程块中的共享内存元素相加，每次分配num_threads/2n个线程，线程编号连续从0到num_threads/（2n-1），避免出现线程分支；③使用一个核函数，分配Block數量为1，负责块内元素求和，得到最终结果。向量点积并行计算方式如图3所示，该算法使线程资源得到充分利用，并且合并访问与存储，达到最大的带宽。

结合上述关键运算，基于CUDA架构的h_MGCG并行程序整体框架如图4所示。

3  数值算例

本节通过1/4圆环和三维悬臂梁这两种经典的数值算例来验证ITO高效求解方法的准确性和高效性。1/4圆环用来验证该求解方法的计算准确性、迭代收敛效果，并与常用求解方法Jacobi共轭梯度法（Jacobi_PCG）、不完全Cholesky分解共轭梯度法（ichol_PCG）、L_MGCG，以及AMG中常用三种不同粗化方式（基于R-S方法的beck_PCG［33］、基于非光滑聚合的HEM_PCG［34］、基于光滑聚合的CW_PCG［35］）的方法进行对比，比较这些求解方法在线性方程组求解时的加速效果。最后，通过三维悬臂梁进一步验证该高效求解方法的通用性，以及在ITO迭代过程中的有效性和高效性。涉及的MGCG中多级矩阵最大层数均设为10，最粗矩阵规模为2000，即MGCG的网格层数达到10或者粗化的矩阵规模小于2000时，不再粗化网格，所有串行和并行程序都采用双精度浮点型运算，测试的计算机CPU型号为Intel Xeon Gold 5218，GPU型号为NVIDIA GeForce RTX 3090。

3.1  1/4圆环

图5给出了1/4圆环的参数设置，其中圆环算例内圆半径为1，外圆半径为2，底边施加固定约束，在左上角施加一个水平向右的集中载荷F=1。

将1/4圆环离散为64×64规模的二阶NURBS单元，在拓扑优化中，体积分数设置为0.5，收敛准则设置为设计变量的最大变化量小于1%或者最大迭代次数为250，不同求解方法的残差均设置为10-10，带权重Jacobi的权重固定为w=0.4，在此算例中，MGCG的网格层数为2。图6所示为用直接法和h_MGCG这两种不同求解方法的拓扑优化最终迭代结果，可以看出h_MGCG求解方

法得到的最终优化结构和直接法的一致，其中本文的直接法采用Cholesky分解。

拓扑优化过程中两种求解方法的柔度变化如图7所示，拓扑优化过程中柔度变化一致，由表3可以看出h_MGCG求得的最终柔度与直接法的最终柔度一致，证明了h_MGCG求解算法的准确性。

将1/4圆环离散为256×256规模的二阶NURBS单元，自由度数目为133 128，并以ITO中第12次迭代的线性方程求解为例，观察求解过程中残差变化。MGCG中光滑处理的Jacobi权重均选取w=0.4，网格层数为4。

图8所示为第12次迭代中不同求解方法求解线性方程的残差变化，可以看出，相比三种基于不同粗化方式的AMG方法，h_MGCG求解方法的收敛速度更快，

by different solving methods

在200次迭代内即可将求解残差收敛到10-10，特别是与传统的Jacobi_PCG方法相比，其迭代次数远远少于Jacobi_PCG方法的5000余次。此外，h_MGCG方法比L_MGCG方法的迭代次数少29，展现出更好的收敛效果。

各种求解方法花费的时间如图9所示。结果表明，相较于其他求解方法，h_MGCG方法更加高效，比L_MGCG方法的速度提高了22.8%，与Jacobi_PCG和ichol_PCG方法相比分别具有16.48和2.60的加速比，与HEM_PCG、CW_PCG、beck_PCG方法相比，其加速比分别为6.20、6.27和6.43。

在求解拓扑优化第12次迭代时，不同多重网格求解方法的并行求解时间如图10所示。结果表明，h_MGCG并行求解方法（GPU_h_MGCG）最为高效，仅需0.328 s即可完成一次求解计算，相比L_MGCG并行求解方法的0.406 s，其求解速度提高了23.8%，也远超三种粗化方式AMG的并行求解速度。同时，GPU_h_MGCG方法相对于串行h_MGCG方法的加速比达到29.65，相对于传统的串行Jacobi_PCG方法，加速比更是高达497.53，证明了h_MGCG方法的高效性。

3.2  三维悬臂梁

为了验证基于ITO的高效求解算法在三维问题上的适用性，本文采用三维悬臂梁算例，比较串行求解方法h_MGCG和并行求解方法GPU_h_MGCG的计算效率，并与其他传统串行求解方法做对比。图11所示为三维悬臂梁的设计域、边界条件、外载荷，对其中一个大小为10×4的端面施加完全约束，在另一端施加密度为1、方向垂直向下的均布线载荷，ITO的体积分数设置为0.3，收敛准则设置为设计变量最大变化量小于1%或者最大收敛次数为250。在求解部分，所有MGCG、AMG中Jacobi权重都选择收敛效果最好的固定权重w=0.3，MGCG层数为3，并将不同求解方法的求解残差设置为10-8。

将三维悬臂梁离散为规模32×16×4的二阶NURBS单元，自由度数目为11 016，不同求解方法在计算线性方程时得到的最终柔度值见表4，可以看出，h_MGCG和GPU_h_MGCG求解方法获得的最终柔度值与直接法的最终柔度值几乎一致。图12所示为三维悬臂梁不同求解方法收敛曲线对比结果，可见h_MGCG方法和直接法求解依然具有几乎相同的优化收敛曲线和结果，证明在三维结构上h_MGCG方法仍然准确。图13所示为用直接法和h_MGCG這两种不同求解方法的三维悬臂梁最终优化结果，可以看到三维算例中h_MGCG求解方法得到的最终优化结果和直接法的最终优化结果仍保持一致。

经过不同算例验证，在ITO过程中，线性方程组的求解占据了大部分时间，占比甚至达90%以上。特别是就三维算例而言，由于刚度矩阵稠密度更高，故求解时间更长。本文对不同求解方法的效率进行比较。如图14所示，在每次ITO的线性方程求解中，h_MGCG方法所需迭代次数明显少于其他传统求解方法，并优于L_MGCG方法，这再次验证了由于h_MGCG方法具有更准确的插值关系而带来的收敛性能的优势。同时，由图15可以看出，在每次迭代中线性方程求解所需时间上，h_MGCG方法也表现出比传统求解方法更高效的特点，特别是相较于Jacobi_PCG方法。

各求解方法在网格规模为32×16×4时ITO的线性方程组总求解时间对比如图16所示，相较于Jacobi_PCG方法，h_MGCG求解方法速度提高了17.02倍，与三种粗化方式AMG求解方法相比提高了9～11倍，相比L_MGCG求解方法则提高了47%。此外，在GPU并行计算的支持下，h_MGCG方法进一步实现加速，并将串行计算所需244.904 s的时间缩短至52.856 s，但其加速比仅为4.63，加速比不大的原因是规模较小。

为了研究网格规模与并行算法加速比之间的关系，图17比较了64×32×8、128×32×8和128×64×16三种网格规模下的GPU_h_MGCG相对于h_MGCG的加速比，三種网格规模自由度数目分别为67 320、13 260和463 320，结果表明，相对于各串行算法，总求解时间的加速比分别为19.89、23.75和33.86。这是由于随着规模的增大，GPU时间开销占据总时间开销的占比变大。因此在处理实际大规模问题时，GPU_h_MGCG求解方法能高效、准确地进行求解，其加速比是串行h_MGCG求解方法加速比的数十倍，是串行PCG求解方法加速比的数百倍甚至更高。

4  结语

本文提出了一种基于h细化的高效多重网格方程求解方法，该方法利用h细化插值得到的粗细网格之间的权重信息构造多重网格方法的插值矩阵，获得比传统的线性插值方法更加准确的网格信息。将该方法与ITO相结合，只需在ITO细化过程中提取一次网格信息，可提高求解效率。同时，结合GPU并行计算，大幅提高ITO中线性方程组的求解速度。从硬件和算法两方面提高求解速度，进而加快ITO求解效率。数值算例表明，h_MGCG求解方法最终的柔度值与直接法求解的结果几乎一致，表明其求解结果能达到精度要求，同时其拓扑优化最终结果也保持一致。与其他求解方法相比，h_MGCG还具有更快的收敛速度和求解速度，与Jacobi_PCG、AMG和L_MGCG相比，取得了最高17.02、11.12和1.47的加速比。此外，结合GPU并行的GPU_h_MGCG求解方法充分利用了计算机资源，使得h_MGCG并行相对串行获得了最高33.86的加速比，与传统求解方法相比提升巨大。在大规模方程求解中，本文方法能够快速高效、准确求解，对求解大规模ITO问题具有重要意义。

虽然本文方法实现了等几何方程的高效求解，但仍有一些工作亟待完善。本文方法在进行平滑处理时，Jacobi迭代法权重的选取上采用了固定最佳权重，而对于不同算例，该最佳权重并不总是相同的。今后会针对不同算例自适应地选取Jacobi迭代法的权重，在增强通用性的同时减少迭代次数，以提高求解效率。此外，结合文献［36］的工作，今后可以较容易地将本文方法扩展到复杂模型的等几何分析之中，为实际工程应用提供更高效的求解方法。

参考文献：

［1］  杨雨豪，郑伟，王英俊.一种自由度缩减和收敛加速的高效等几何拓扑优化方法［J］.中国机械工程，2022，33（23）：2811-2821.

YANG Yuhao， ZHENG Wei， WANG Yingjun. An Efficient Isogeometric Topology Optimization Methods Using DOF Reduction and Convergence Acceleration［J］. China Mechanical Engineering， 2022， 33（23）：2811-2821.

［2］  BENDSE M P. Optimal Shape Design as a Material Distribution Problem［J］. Structural Optimization， 1989， 1（4）：193-202.

［3］  BENDSE M P， KIKUCHI N. Generating Optimal Topologies in Structural Design Using a Homogenization Method［J］. Computer Methods in Applied Mechanics and Engineering， 1988， 71（2）：197-224.

［4］  ALLAIRE G， JOUVE F， TOADER A-M. ALevel-set Method for Shape Optimization［J］. Comptes Rendus Mathematique， 2002， 334（12）：1125-1130.

［5］  QUERIN O M， STEVEN G P， XIE Y M. Evolutionary Structural Optimisation（ESO） Using a Bidirectional Algorithm［J］. Engineering Computations， 1998， 15（8）：1031-1048.

［6］  GUO X， ZHANG W， ZHANG J， et al. ExplicitStructural Topology Optimization Based on Moving Morphable Components（MMC） with Curved Skeletons［J］. Computer Methods in Applied Mechanics and Engineering， 2016， 310：711-748.

［7］  WANG Chuang， ZHU Jihong， WU Manqiao， et al. Multi-scale Design and Optimization for Solid-lattice Hybrid Structures and Their Application to Aerospace Vehicle Components［J］. Chinese Journal of Aeronautics， 2021， 34（5）：386-398.

［8］  GAO B， MENG D， SHI W， et al. Topology Optimization and the Evolution Trends of Two-speed Transmission of EVs［J］. Renewable and Sustainable Energy Reviews， 2022， 161：112390.

［9］  BRANDO P， SILVA P T， PARENTE M， et al. μSmartScope—Towards a Low-cost Microscopic Medical Device for Cervical Cancer Screening Using Additive Manufacturing and Optimization［J］. Proceedings of the Institution of Mechanical Engineers， Part L：Journal of Materials：Design and Applications， 2022， 236（2）：267-279.

［10］  LI Y， LAI Y， LU G， et al. Innovative Design of Long-span Steel-concrete Composite Bridge Using Multi-material Topology Optimization［J］. Engineering Structures， 2022， 269：114838.

［11］  丁延冬，羅年猛，杨奥迪，等.Bézier单元刚度映射下的高效多重网格等几何拓扑优化方法［J］.中国机械工程，2022，33（23）：2801-2810.

DING Yandong， LUO Nianmeng， YANG Aodi， et al. Efficient Multigrid Isogeometric Topology Optimization under Bézier Element Stiffness Mapping［J］. China Mechanical Engineering， 2022， 33（23）：2801-2810.

［12］  HUGHES T J R， COTTRELL J A， BAZILEVS Y. Isogeometric Analysis：CAD， Finite Elements， NURBS， Exact Geometry and Mesh Refinement［J］. Computer Methods in Applied Mechanics and Engineering， 2005， 194（39/41）：4135-4195.

［13］  SEO Y D， KIM H J， YOUN S K. IsogeometricTopology Optimization Using Trimmed Spline Surfaces［J］. Computer Methods in Applied Mechanics and Engineering， 2010， 199（49/52）：3270-3296.

［14］  KUMAR A V， PARTHASARATHY A. Topology Optimization Using B-spline Finite Elements［J］. Structural and Multidisciplinary Optimization， 2011， 44（4）：471-481.

［15］  GAO J， WANG L， LUO Z， et al. IgaTop：an Implementation of Topology Optimization for Structures Using IGA in MATLAB［J］. Structural and Multidisciplinary Optimization， 2021， 64（3）：1669-1700.

［16］  WANG Y， WANG Z， XIA Z， et al. Structural Design Optimization Using Isogeometric Analysis：a Comprehensive Review［J］. Computer Modeling in Engineering & Sciences， 2018， 117（3）：455-507.

［17］  GAO J， XIAO M， ZHANG Y， et al. A Comprehensive Review of Isogeometric Topology Optimization：Methods， Applications and Prospects［J］. Chinese Journal of Mechanical Engineering， 2020， 33（6）：34-47.

［18］  NAGY A P， ABDALLA M M， GURDAL Z. Isogeometric Sizing and Shape Optimization of Beam Structures［J］. Computer Methods in Applied Mechanics and Engineering， 2010，199：1216-1230.

［19］  NGUYEN D M，ANTON E，ALLAN R G，et al. Isogeometric Shape Optimization of Vibrating Membranes［J］. Computer Methods in Applied Mechanics and Engineering， 2011， 200：1343-1353.

［20］  YOUN D H， KIM M G， KIM H S. Shape Design Optimization of SPH Fluid-structure Interactions Considering Geometrically Exact Interfaces［J］. Structural and Multidisciplinary Optimization， 2011， 44：319-336.

［21］  刘宏亮，祝雪峰，杨迪雄.基于等几何分析的结构优化设计研究进展［J］.固体力学学报，2018，39（3）：248-267.

LIU Hongliang， ZHU Xuefeng， YANG Dixiong. Research Advances in Isogeometric Analysis-based Optimum Design of Structure［J］. Chinese Journal of Solid Mechanics， 2018， 39（3）：248-267.

［22］  AAGE N， ANDREASSEN E， LAZAROV B S， et al.Giga-voxel Computational Morphogenesis for Structural Design［J］. Nature， 2017， 550（7674）：84-86.

［23］  THOMAS S J， ANANTHAN S， YELLAPANTULA S， et al. AComparison of Classical and Aggregation-based Algebraic Multigrid Preconditioners for High-fidelity Simulation of Wind Turbine Incompressible Flows［J］. SIAM Journal on Scientific Computing， 2019， 41（5）：S196-S219.

［24］  刘石，陈德祥，冯永新，等.等几何分析的多重网格共轭梯度法［J］.应用数学和力学，2014，35（6）：630-639.

LIU Shi， CHEN Dexiang， FENG Yongxin， et al. A Multigrid Preconditioned Conjugate Gradient Method for Isogeometric Analysis［J］. Applied Mathematics and Mechanics， 2014， 35（6）：630-639.

［25］  WANG Y， LIAO Z， YE M， et al. An Efficient Isogeometric Topology Optimization Using Multilevel Mesh， MGCG and Local-update Strategy［J］. Advances in Engineering Software， 2020， 139：102733.

［26］  邓亮，徐传福，刘巍，等.交替方向隐式CFD解法器的GPU并行计算及其优化［J］.计算机应用，2013，33（10）：2783-2786.

DENG Liang， XU Chuanfu， LIU Wei， et al. Parallelization and Optimization of Alternating Direction Implicit CFD Solver on GPU［J］. Journal of Computer Applications， 2013， 33（10）：2783-2786.

［27］  XIA Z， WANG Y， WANG Q， et al. GPU Parallel Strategy for Parameterized LSM-based Topology Optimization Using Isogeometric Analysis［J］. Structural and Multidisciplinary Optimization， 2017， 56：413-434.

［28］  韓琪，蔡勇.基于GPU的大规模拓扑优化问题并行计算方法［J］.计算机仿真，2015，32（4）：221-226.

HAN Qi， CAI Yong. An Efficient Parallel Implementation of Large-scale Topology Optimization Problems Using GPU［J］. Computer Simulation， 2015， 32（4）：221-226.

［29］  AVNAT O， YAVNEH I. On the Recursive Structure of Multigrid Cycles［J］. SIAM Journal on Scientific Computing， 2022（V3）：S103-S126.

［30］  MADAMS A， SIFAKIS E， TERAN J. A Parallel Multigrid Poisson Solver for Fluids Simulation on Large Grids［C］∥Proceedings of the 2010 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Madrid，2010：65-74.

［31］  LIU Y， SCHMIDT B. Lightspmv：Faster Cuda-compatible Sparse Matrix-vector Multiplication Using Compressed Sparse Rows［J］. Journal of Signal Processing Systems， 2018， 90：69-86.

［32］  LIU Y， GONZLEZ-DOMNGUEZ J， SCHMIDT B. Faster Compressed Sparse Row（CSR）-based Sparse Matrix-vector Multiplication Using CUDA［C］∥GPU Technology Conference. Silicon Valley， 2015：17-20.

［33］  BECK R. Algebraic Multigrid by Component Splitting for Edge Elements on Simplicial Triangulations［R］. ZIB-Report（SC-99-40），1999.

［34］  NOTAY Y. Aggregation-based Algebraic Multigrid for Convection-diffusion Equations［J］. SIAM Journal on Scientific Computing， 2012， 34（4）：A2288-A2316.

［35］  BERNASCHI M， DAMBRA P， PASQUINI D. AMG Based on Compatible Weighted Matching for GPUs［J］. Parallel Computing， 2020， 92：102599.

［36］  WANG Y， GAO L， QU J， et al. Isogeometric Analysis Based on Geometric Reconstruction Models［J］. Frontiers of Mechanical Engineering， 2021，16：782-797.

（編辑  陈  勇）

作者简介：

杨  峰，男，1998年生，硕士研究生。研究方向为拓扑优化、GPU并行计算。

王英俊（通信作者），男，1984年生，教授、博士研究生导师。研究方向为拓扑优化、等几何分析、CAD/CAE一体化。E-mail：wangyj84@scut.edu.cn。