基于分类-关联-修正的电力需求预测方法研究

杨 萌,邓振立,李虎军,邓方钊,李文琦,孙伟卿

(1.国网河南省电力公司经济技术研究院,河南 郑州 450052;2.上海理工大学机械工程学院,上海 200093)

0 引言

电力行业作为碳排放较高的行业,在新时代“双碳”背景以及电力市场化改革背景下,亟需进行绿色低碳转型[1]。近年来,我国电力行业发展成效显著,但也出现了一些新问题和新风险。电力供需总体上处于紧张状态。尤其在夏季和冬季用电高峰时期,电力出现了一定范围内的供需失衡局面。这严重阻碍了我国社会经济的可持续发展。因此,在电力供需矛盾日趋加剧的今天,对电力行业的电力需求形势进行预测具有重要的现实意义。

针对电力需求预测,国内外众多学者已经开展了大量研究。文献[2]探究了新时代背景下南通市电力需求的变化特点和影响因素,对南通市电力需求进行灰色预测,并提出了有助于电力发展的相关建议。文献[3]借助果蝇算法对支持向量机模型参数进行优化,并通过季节指数对预测的中美两国电力需求量结果进行修正,从而提高预测精度。文献[4]采用灰色预测模型对中国电力需求进行预测分析,并借助粒子群算法优化模型大幅提高了预测精度。文献[5]使用差分进化法将误差反向传播(back propagation,BP)神经网络、模糊推断系统和季节差分算法进行赋权集成,建立预测模型以对电力需求序列进行预测,从而取得了更好的预测效果。文献[6]采用先进计量基础设施(advanced metering infrastructure,AMI)分析智能电表数据,提高了短期预测的准确性。文献[7]利用灰色关联模型对电力需求的影响因素进行分析,构建了基于灰色预测和粒子群优化-极限学习机的电力需求组合预测模型,取得了更高的预测精度,并预测了吉林省“十四五”期间的电力需求量。

上述文献采用了众多预测方法对电力需求形势进行预测。这些方法大多利用预测算法直接对总电力需求进行预测,而缺乏对总电力需求进行分类并单独预测的研究,不能很好地体现各行业用电需求特性。

本文首先利用灰色关联分析方法筛选出与全社会用电量关联程度较大的三类产业用电,并建立回归分析方程;其次,分别选出对上述三类产业用电影响程度较大的三个影响因素,并分别建立产业用电与影响因素的回归分析方程;然后,以产业电量占全社会电量的比值作为修正系数,提高了模型的预测精度;最后,采用灰色预测方法获得各影响因素的预测值,并结合产业用电回归方程和电量占比系数得到电力需求预测结果。

1 电力需求量预测模型

1.1 灰色关联分析方法

灰色关联分析方法是一种多因素统计数据分析方法。该方法根据各因素的样本数据计算灰色关联度,并以该关联度指标来描述所选样本因素间的关系,包括强弱、大小和次序关系等。由于影响电力供需变化的因素复杂且众多,灰色关联分析方法可以从众多影响因素中筛选出影响程度较大的几个因素,并以此作为后续回归分析时的指标。

灰色关联分析方法进行影响因素分析的一般过程如下。

①确定反映系统行为特征的母序列X0和影响系统行为的子序列Xi。

X0=[x0(1),x0(2),…,x0(n)]

(1)

式中:n为母序列中元素的个数。

Xi=[xi(1),xi(2),…,xi(n)],i=1,2,…,m

(2)

式中:m为子序列的总数。

②对数据进行无量纲化处理,求得各序列的初值像。

无量纲化有两种方法,分别为初值化和均值化。

初值化:

(3)

式中:Xi(1)为原始子序列中的第一个值。

均值化:

(4)

③计算关联系数。

(5)

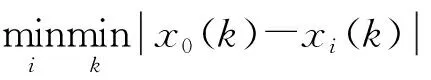
④计算灰色关联度。

(6)

式中:γ0i为xi对x0的综合关联系数值。

⑤根据灰色关联度的大小对影响因素进行排序。关联度值越大,则影响因素对目标的影响程度越高。

1.2 回归分析方法

回归分析方法是一种确定两种或两种以上变量间相互依赖的定量关系的统计分析方法。由于影响电力需求的因素很多,本文主要采用多元线性回归分析方法。预测目标y受p个影响因素x1,x2,…,xp的影响。多元线性回归模型表达式为:

y=a0+b1x1+b2x2+…+bpxp

(7)

式中:xp为可控变量;a0和b1,b2,…,bp均为模型参数。

对x1,x2,…,xp进行q次观测,可得q组观测值(xi1,xi2,…,xip,yi)(i=1,2,…,q),即:

(8)

未知参数a0和b1,b2,…,bp的值可用最小二乘法求解。这些未知参数代入原方程后,得到的回归分析方程为:

(9)

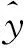
1.3 灰色预测方法

灰色预测方法通过对原始数据序列的整理,建立累加和累减数列,进而建立相应的微分方程以获得数据序列的发展趋势,从而对未来的数据进行预测。常用的灰色预测模型为GM(1,1)模型。GM(1,1)模型建模步骤如下。

长度为n′的时间数值序列设时间序列X(0)为:

X(0)=[x(0)(1),x(0)(2),…,x(0)(n′)]

(10)

X(0)中的值依次累加得到长度为n′的时间数值序列X(1)。

X(1)=[x(1)(1),x(1)(2),…,x(1)(n′)]

(11)

X(1)的紧邻均值生成序列Z(1)为:

Z(1)=[z(1)(1),z(1)(2),…,z(1)(n′)]

(12)

Z(1)为用均值生成方法填补原非等时序列而生成的等时序列。

GM(1,1)模型的灰微分方程模型为:

x(0)(s)+ez(1)(s)=g

(13)

式中:e为发展系数;g为灰色作用量;s=2,3,…,n′。

利用最小二乘法求解微分方程,可得灰色预测方程为:

(14)

2 算例分析

2.1 电力需求影响因素分析

电力需求变化受政治、经济、生活水平等各方面因素的影响,存在影响因素众多、影响机理复杂的特点。因此,在进行电力需求预测过程中,要考虑各种相关因素对电力需求的影响。例如:国内生产总值(gross domestic product,GDP)的变化与电力需求的变化正相关;电价的波动会影响高耗能企业的生产成本,从而影响用电情况[8]。而在进行电力需求预测过程中,要根据预测的实际情况选择合适的数据。例如,文献[9]选取GDP、城镇化水平、工业化水平、人口数量、产业结构、居民消费水平、电价和用电基数作为影响电力需求的因素,从中筛选出关键影响因素以建立电力需求预测模型。因此,不同的预测方法需要选取不同的自变量数据。

本文按产业用电将全社会用电量分为五类,分别为第一产业用电、第二产业用电、第三产业用电、城镇居民用电和乡村居民用电。在对电力需求进行分析时,本文选取了河南省几个能够明显影响电力需求、方便进行定量化处理、易于获取系统行为特征的数据序列的因素进行各产业用电关联度分析。选取的影响因素分别为GDP、人口数、居民人均可支配收入、固定资产投资总额、城市化水平[10]。本文选取了2011—2021年的上述因素数据。这些数据可在国家能源局河南监管办公室网站以及河南省统计年鉴中查询得到。出于数据保密性的考虑,本文对所有真实电力数据乘以了一个系数。

2.2 产业用电灰色关联分析及回归分析

本文利用灰色关联分析方法分析第一产业用电、第二产业用电、第三产业用电、城镇居民用电、乡村居民用电与全社会用电量的关联程度,得到各产业用电的关联度和关联序。产业用电灰色关联分析如表1所示。

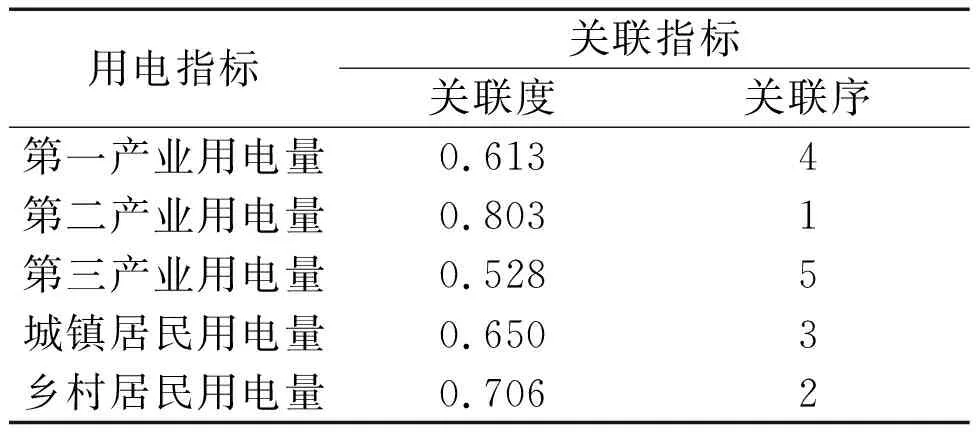
表1 产业用电灰色关联分析表

由表1可知,产业用电与全社会用电量的关联程度由高到低依次为第二产业用电量、乡村居民用电量、城镇居民用电量、第一产业用电量、第三产业用电量。因此,本文选取关联程度较大的第二产业用电量、乡村居民用电量和城镇居民用电量,建立与全社会用电需求的多元回归方程。

E=C+x1×N1+x2×N2+x3×N3

(15)

式中:C为后验差比;N1为第二产业用电量,亿千瓦时;N2为乡村居民用电量,亿千瓦时;N3为城镇居民用电量,亿千瓦时。

本文利用2011—2021年的产业用电数据对模型进行基于最小二乘法的线性回归分析,得到的线性回归方程为:

E=9.635 62+1.011 454×N1-1.641 601×N2+5.920 340×N3

(16)

2.3 影响因素灰色关联分析及回归分析

本文选取的数据有GDP、居民人均可支配收入和固定资产投资总额等经济性指标,并且所选数据的时间跨度较大,因此指标会受到实际通货膨胀的影响,从而对关联性分析带来一定影响。为此,本文在进行灰色关联分析计算时,已将通货膨胀影响纳入考虑,并对数据作了相应处理。本文利用灰色关联分析理论,分别对N1、N2、N3与GDP、人口数、居民人均可支配收入、固定资产投资总额等影响因素进行灰色关联分析,从而得到各产业用电需求与各指标的灰色关联度与关联序。

影响因素灰色关联分析如表2所示。

表2 影响因素灰色关联分析表

由表2可知:与N1关联程度较大的三个影响因素为人口数、城市化水平、居民人均可支配收入;与N2和N3关联程度较大的三个因素均为GDP、居民人均可支配收入和全社会固定投资总额。因此,本文分别对各产业用电与关联程度较大的三个影响因素建立多元回归分析方程,并利用最小二乘法求解。

N1=-3 519.340 941+0.604 567×f2-29.287 189×f5+0.031 917×f3

(17)

式中:f2为人口数,万;f3为居民人均可支配收入,元;f5为城市化水平,%。

N2=-90.718 531+0.027 787×f1+0.007 888×f3-0.015 271×f4

(18)

式中:f1为GDP,亿元;f4为全社会固定资产投资总额,亿元。

N3=-115.293 128+0.031 219×f1-0.002 360×f3-0.014 791×f4

(19)

2.4 影响因素灰色预测

为了获得未来全社会的电力需求量,必须先获取各影响因素的未来预测数据。本文采取灰色预测的方法对各影响因素进行预测。

灰色预测模型构建参数如表3所示。

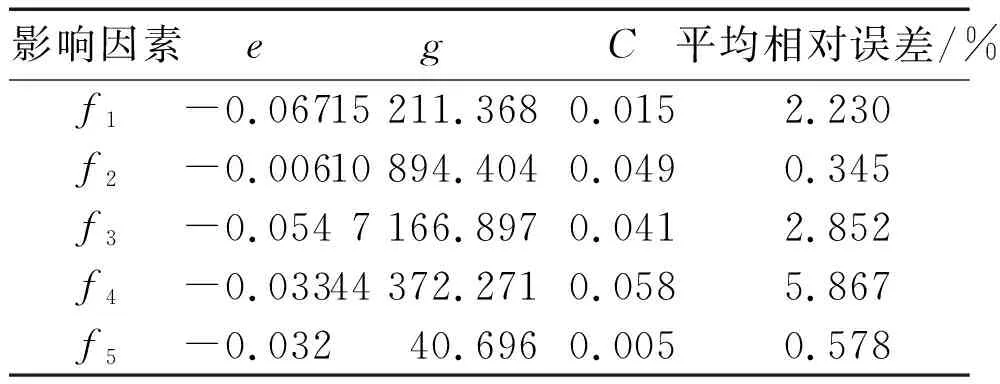
表3 灰色预测模型构建参数

将表3的C值与灰色模型预测精度检验等级参照表对照可知,各影响因素的灰色预测模型精度高。由平均相对误差可知模型拟合效果良好。因此,本文构建的灰色预测模型符合要求。

2.5 电量占比修正系数

本文建立的电力需求回归预测模型采用全社会电力需求量与第二产业用电、乡村居民用电和城镇居民用电进行回归。由于所选取的产业用电在每年全社会总电力需求量中的占比都不相同,利用此模型进行预测会导致部分误差。因此,本文采用第二产业用电、乡村居民用电和城镇居民用电占全社会用电需求的电量比例作为修正系数,进一步提高预测结果的精度。本文采用二次多项式拟合模型对2011—2021年的电量占比系数进行拟合。拟合模型为:

r=-0.001 221×t2+0.005 165×t-0.884 730

(20)

式中:r为电量占比系数;t为年份,表示自2011年开始的年数。本文设2011年为t=1、2012年为t=2,以此类推。

2.6 电力需求预测

本文构建的灰色预测模型、各产业用电回归预测模型以及二次多项式拟合模型可以对电力需求进行预测。

本文将2022年的N1、N2、N3预测数据代入式(16),可得多元回归预测中2022年全社会电力需求量为5 675.893亿千瓦时。这个结果与2022年实际全社会用电量5862.27亿千瓦时的误差为3.179%。利用2022年的N1、N2、N3和r预测数据计算得到2022年全社会电力需求量为5 847.118亿千瓦时,与实际用电量误差为0.258%。由此可知,采用电量占比预测电力需求量可减小每年各产业用电占比的不同而带来的误差,进一步提高预测结果的准确性。

2022—2026年影响因素及产业用电预测数据如表4所示。

表4 2022—2026年影响因素及产业用电预测数据

由表4可知,2023—2026年的全社会电力需求量分别为6 209.653、6 635.171、7 137.113、7 732.190亿千瓦时。经过对电力需求的预测分析,以及对历史用电形势的总体判断,所研究地区电力需求的总体水平将保持平稳增长,且到2025年将突破7 000亿千瓦时。基于此,可提前制定合适的电力生产计划。

3 结论

在进行电力需求预测时,影响电力需求预测的因素较多、影响机理复杂、影响程度不同。基于以上特点,本文提出一种基于分类-关联-修正的电力需求预测方法。该方法首先按照产业用电量将全社会用电量分为五类;其次,利用灰色关联分析方法选取关联程度较大的三类产业用电;然后,利用灰色关联分别筛选出对三类产业用电影响程度较大的三个因素,并建立回归预测方程;最后,利用产业电量占比作为修正系数对电力需求进行预测。该方法提高了预测结果精度、保证了预测结果的准确性,对于制定电力生产计划有一定的指导作用。本文在采用灰色预测对全社会固定资产投资总额进行预测时的误差相对较大。后续研究可采用其他更适合的预测方法,从而进一步提高预测的准确性。