电力通信数据流量异常的并行检测方法设计
2024-05-07刘璐
刘 璐
(北京科东电力控制系统有限责任公司,北京 100192)
0 引言
电力通信数据技术被广泛应用于智能电网的设计中[1]。为了创造安全、高效的电力通信网络运营环境,通信数据流量的异常监测技术已成为电力工作人员的研究重点[2]。姜丹等[3]首先采用大数据分析技术得到电力通信数据流量的最大似然值;然后构建数据流量异常监测模型,并通过子序列聚类处理最大似然值得到异常流量的特征;最后将特征输入到异常监测模型中,从而完成电力通信数据流量的异常监测。周伯阳等[4]首先构建基于多尺度低秩序的电力数据异常监测模型;然后对电力通信数据流量作归一化处理,并采用改进的递归特征选择法得到流量的聚类结果;最后将聚类结果输入到监测模型中进行分类,从而完成电力通信数据流量的异常监测。孙滢涛等[5]首先根据趋势性、动态性和变换性,分别提取电力通信数据流量的特征;然后对特征作降噪处理;最后采用支持向量数据构造一类分类器模型,并将特征输入到模型中,从而完成电力通信数据流量的异常监测。数据流量的异常监测是电力通信网络使用过程中不可缺少的环节。但该环节受不同信道流量冗余性、异常数据类型等问题的干扰,导致监测过程耗时长且误差大。
为了进一步优化电力通信数据流量异常监测过程,本文设计电力通信数据流量异常的并行检测方法。本文在对电力通信数据流量降维的基础上:采用并行分解传感算法,对多信道数据流量进行并行分解;采用并行检测算法,实现了电力通信数据流量异常监测。试验结果表明,本文方法具有较好的监测效果,有助于保证电力通信网络运营环境的通信质量。
1 数据流量的处理
1.1 数据流量的降维处理
为了保证电力通信数据流量具有良好的并行分解效果,本文采用自适应邻域法对数据流量作降维处理。具体步骤如下。
①通过自适应邻域法选取所有电力通信数据流量样本点的e个近邻点,计算任意两个样本点间的欧式距离[6]。
(1)
式中:a、b均为电力通信数据流量的样本点;D为数据流量样本点之间的欧氏距离;M为样本点的总数量,个。
②对欧氏距离作优化处理[7],并结合限制条件计算出数据流量的局部重建权值矩阵,将电力通信数据流量的降维过程转换为寻找最优解问题。
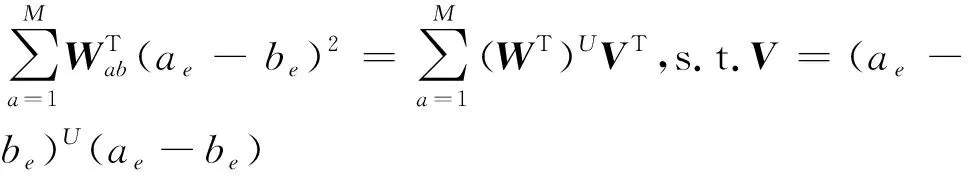
(2)
式中:V为局部协方差矩阵;W为重建权值矩阵;U为限制条件;α为优化系数。
③引入拉格朗日乘子[8],解决式(2)中的限制条件。
(3)
式中:β为算法迭代次数,次;K为引入的拉格朗日乘子。
④通过寻找最优解问题,将高维度的电力通信数据流量映射到低维度空间,以完成数据流量的降维处理。这不仅使降维后的数据流量保留了原始的内部特征,还为后续的并行分解处理创造出更具体的可分性。
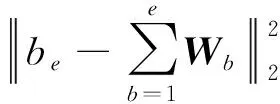
(4)
式中:minα(b)为最优求解结果;L为单位矩阵;s.t.bU为在bU=L的条件下进行寻优;bU为电力通信数据流量样本点b在限制条件U下的降维处理过程中的特征参数。
1.2 多信道数据流量的并行分解
针对降维后的电力通信数据流量,本文在变换矩阵的基础上[9]采用并行分解传感算法实现多信道数据流量的并行分解,从而有效地降低数据流量的冗余性。具体步骤如下。
①设降维后的电力通信数据流量维度为B、其对应的列向量为J、在变换矩阵的作用下系数向量的维度为P。则在维度为B×P的变换矩阵C下,数据流量为:
(5)
式中:Z为电力通信数据流量在变换矩阵中的系数向量。
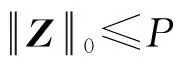
③在电力通信数据流量满足稀疏表达后,引入传感矩阵T,将数据流量通过传感矩阵进行投影[10]。
φ=TJ=TCZ
(6)
式中:φ为解压后的电力通信数据流量,GB。
④独特的数据流量分解由若干棵随机二叉树构成。
随机二叉树划分过程如图1所示。
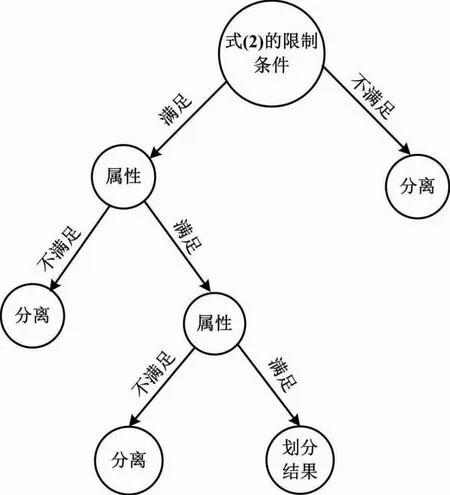
图1 随机二叉树划分过程
通过随机抽样一致算法[11]从电力通信数据流量集合中选取m个样本点构成子集I,并从其中随机抽选一个属性A与分离值z。
I=[I1,I2,…,Im],A,z∈Im
(7)
属性A从电力通信数据流量样本四类属性中随机选取。第一类属性为基本特征,主要包括连续时间、协议类型和传输字节数等。第二类属性为内容特征。第三类属性为基于时间的网络流量统计特征。第四类属性为基于主机的网络流量统计特征。
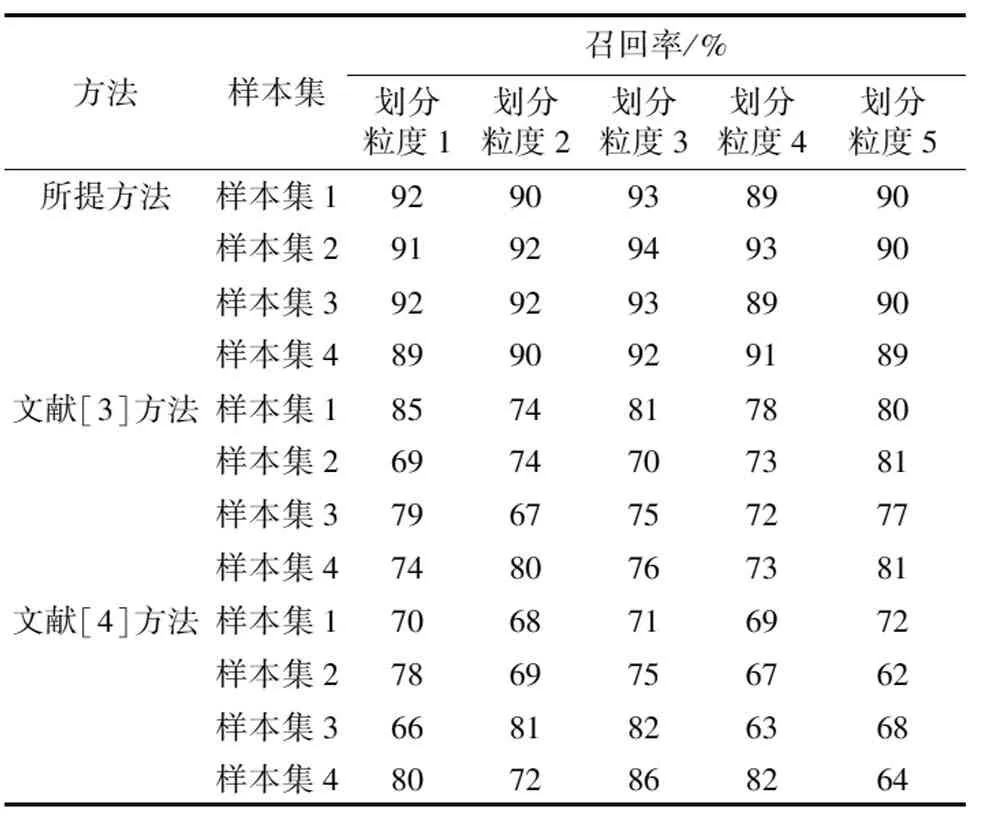
⑤考虑到基本特征属性可以更好地判断电力通信数据流量是否存在异常,本文将式(7)中随机选取的属性A定义为基本特征属性。在随机二叉树中,根据基本特征属性值和分离值对所有电力通信数据流量样本点实行并行划分。若Im(A) ⑥在随机二叉树的每次划分过程中,本文采用随机生成的超平面构造一个分离超平面,以保证分解的高效运行。 (8) 式中:u为随机系数;Ai为第i个属性值;d为分离超平面;ε为属性之间的标准差;r为属性指标。 本文针对并行分解后的电力通信数据流量,设计并行检测算法,以完成数据流量的异常监测。 电力通信数据流量异常的并行检测流程如图2所示。 图2 电力通信数据流量异常的并行检测流程图 并行检测步骤如下。 ①确定电力通信数据流量的并行划分粒度。假设在并行检测过程中单个数据流量的检测时间相同,则总耗时由并行任务的解压耗时与衍生耗时构成。 (9) 式中:t为并行检测过程的总耗时,s;E为并行分解的数据流量总数,GB;x为衍生耗时,s;G为单个并行检测的消耗时间,s;N为检测任务总量,个;R为并行分解数据流量的体积;Q为划分粒度,维。 ②在并行检测过程中,引入常量δ以表示Q与t之间的关联,即可得到Q与t的关系。 (10) 式中:S为并行检测算法的复杂度,%。 ③将经过划分的电力通信数据流量传输到分布式计算框架中,同时成立节点协作传输策略,对所有划分块作检测处理。 ④当分布式计算框架中所有节点完成检测任务时,将结果汇总至框架的主节点中,从而完成电力通信数据流量的并行检测输出[12]。 (11) 式中:O为电力通信数据流量的并行检测输出。 本文将并行检测处理后的电力通信数据流量输入到孤立森林模型,通过寻找出与大部分数据流量不同的样本点,并将这些样本点视为异常点,从而完成数据流量的异常监测。 ⑤根据随机二叉树叶子节点到根节点的路径长度来寻找电力通信数据流量中的异常值。路径的数量由随机二叉树的根节点与叶子节点经过的边的数量决定。 (12) 式中:φ为欧拉常数,φ≈0.577 2;g为路径的数量,条;L′为路径长度。 ⑥路径长度可以反映数据流量样本点的异常离群状况。a的异常得分k为: (13) 式中:H为样本点在随机森林模型中的离群度。 ⑦当k值趋近于0.5时,表明电力通信数据流量样本中不存在异常现象;当k值趋近于1时,表明此时对应的样本点是一个异常值。 为了验证电力通信数据流量异常的并行检测方法的整体有效性,本文需要进行以下测试。 测试使用四组不同的电力数据流量样本集作为试验数据。这四组数据均来自辽宁省某电力公司2020年的分布式控制系统(distributed control system,DCS)运营数据。其编号分别为数据流量集1~4。试验以均方误差、时间消耗、召回率作为评价指标,采用所提方法、文献[3]方法和文献[4]方法完成对比测试。 通过所提方法对电力通信数据并行分解,并比较分解后的数据与原始数据的区别,判断重构信号是否可以客观地反映原始电力网络异常数据信号的特征。异常数据并行分解试验结果如图3所示。 图3 异常数据并行分解试验结果 由图3可知,所提方法重构后的异常数据基本上还原了原始数据原貌,只是在细节上的数据有所损失。由图3(b) 、图3(c)可知,在并行分解过程中,所提方法较为完整地保存了平缓区和突变区的信号,说明所提方法可以有效分解异常数据。 ①均方误差。 均方误差描述方法监测结果与真实结果之间的差距。其值越大,表明方法的拟合能力越弱、监测结果偏差越大;其值越小,表明方法的拟合能力越强、监测结果偏差越小。 (14) 式中:MSE为均方误差;n为电力通信数据流量的数量;Xj为第j个输入样本;F(Yj)为各方法的监测结果。 不同方法的均方误差测试结果如表1所示。 表1 不同方法的均方误差测试结果 由表1可知,针对电力通信数据流量的监测,无论在哪组数据流量集中,所提方法的均方误差均小于文献[3]方法与文献[4]方法。这表明所提方法的拟合效果更好、监测结果更精准。 ②时间消耗。 时间消耗指各方法在电力通信数据流量异常监测过程中所消耗的时间。时间消耗越大,说明方法的监测性能越低;时间消耗越小,说明方法的监测性能越高。在数据监测中,拉格朗日乘子用于处理带有时间约束的电力通信数据流量异常监测问题。如果将拉格朗日乘子看作一个惩罚项,则拉格朗日乘子越高,对违反时间约束的数据的惩罚越严厉,因此监测时间越长。 不同方法的时间消耗测试结果如表2所示。由表2可知,针对电力通信数据流量的异常监测,所提方法的时间消耗在45 s附近波动,而文献[3]方法与文献[4]方法的时间消耗分别在75 s和56 s附近波动。不同拉格朗日乘子下,所提方法的时间消耗均小于文献[3]方法与文献[4]方法。这说明所提方法的监测性能高于文献[3]方法与文献[4]方法。 表2 不同方法的时间消耗测试结果 所提方法在对电力通信数据流量的异常监测过程中,采用自适应邻域选择法对数据流量作了降维处理,并采用并行分解传感算法实现数据流量的并行分解。预处理后的数据流量便于传输与存储,进一步降低了时间消耗。 ③召回率。 召回率用来衡量各方法监测出异常数据流量的能力。召回率越高,表明方法的异常监测能力越强;召回率越低,表明方法的异常监测能力越弱。 (15) 式中:R为召回率,%;K′为被监测错误的数据流量数量;T′为正确监测的数据流量数量。 不同方法的召回率测试结果如表3所示。 表3 不同方法的召回率测试结果 由表3可知,针对电力通信数据流量的异常监测,无论在哪组测试样本集中,所提方法的召回率均高于89%。其相较于文献[3]方法、文献[4]方法的召回率更高。这是由于所提方法采用并行检测方法处理数据流量,并将预处理后的电力通信数据流量输入到构建的孤立森林异常监测模型,提高了数据流量异常监测能力。 电力通信数据流量监测过程中,受数据冗余的影响,产生了均方误差大、时间消耗长、召回率高等问题。为此,本文提出电力通信数据流量异常的并行检测方法。该方法首先采用自适应邻域算法对电力通信数据流量作降维处理,并采用并行分解传感算法实现数据流量的并行分解;其次采用并行检测方法处理数据流量;最后将预处理后的电力通信数据流量输入孤立森林异常监测模型中,从而完成电力通信数据流量的异常监测。试验结果表明,该方法不仅降低了电力通信数据流量监测过程中的均方误差和时间消耗,也在一定程度上提高了召回率。2 数据流量的并行检测
3 试验与分析
3.1 试验设置
3.2 并行分解试验
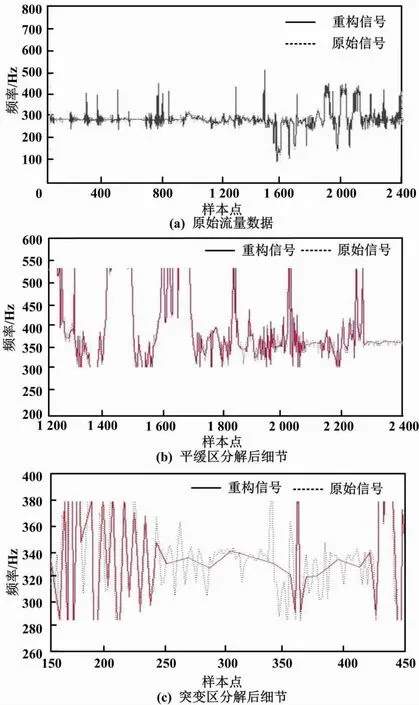
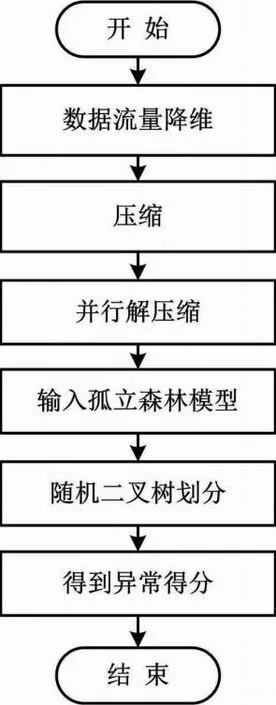
3.3 异常数据检测试验结果分析
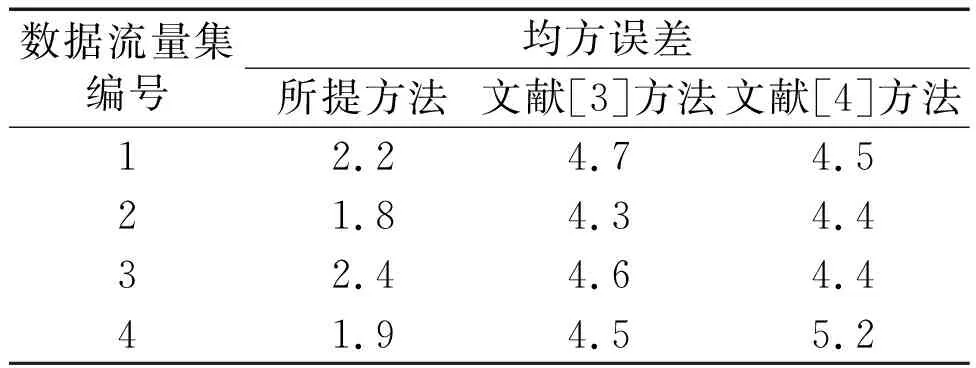
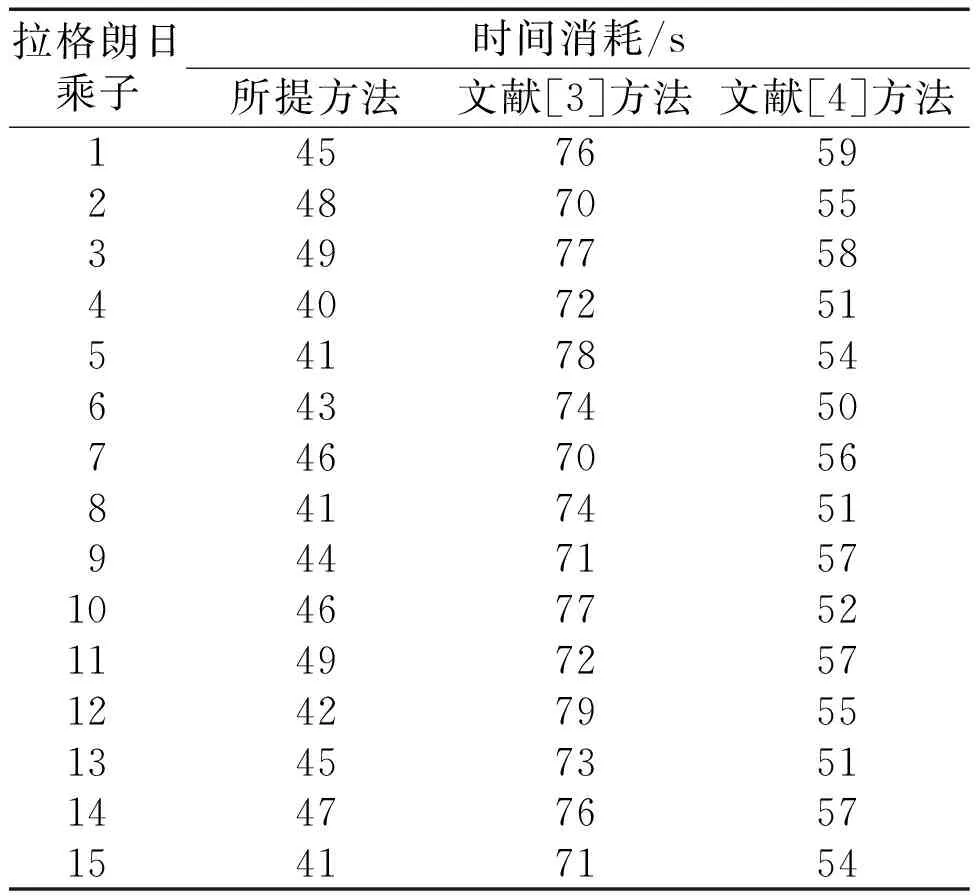
4 结论
