电力工程数据自动分类提取与分析技术研究
2024-05-07雷振华李小云陈屹东陈芃起李雯乐
雷振华,李小云,陈屹东,陈芃起,李雯乐
(湖南省电力有限公司经济技术研究院,湖南 长沙 410007)
0 引言
随着大数据时代的来临,各行业的数据量均在急剧增加。为了促进双碳目标的实现,电网的建设速度持续加快且项目种类愈加丰富,导致电力工程数据的规模越来越大、类型也更为复杂。由于传统的数据管理方法已无法满足当前电力工程的需求,亟需一种新的方法来实现对相关数据的分类和处理[1-2]。目前常用的数据分析管理算法主要有聚类和分类两种,包含K-means聚类、K-Medodis聚类、朴素贝叶斯(naive Bayes,NB)分类以及K最近邻(K-nearest neighbor,KNN)分类算法等[3-6]。文献[7]利用K-means算法对电力工程数据进行了聚类分析研究。该算法能够有效提高数据分类的效率。但传统K-means聚类的K值选取存在不确定性,同时电力数据与簇中心点的相关性也偏弱。这会导致分类结果出现较大误差,从而影响数据分类结果的准确性。
为了解决上述问题,本文提出了1种基于改进K-means聚类算法和长短期记忆(long short-term memory,LSTM)神经网络的电力工程数据自动分类提取与分析技术。首先,本文基于阈值判定来选择K值,即将每个应用场景聚类所设置的阈值进行对比,选择出理想的K值,并使其与电力工程的数据相匹配。其次,本文采用属性加权法对空间距离进行优化,并通过对数据点间的距离赋予附加权值来进一步凸显数据之间的关联程度。最后,本文利用LSTM神经网络对数据间的特征进行自适应学习,从而实现工程数据的分析与预测。
1 K-means聚类算法的改进
1.1 K-means聚类算法
K-means是1种基于划分思想的典型聚类算法。其主要原理是将原始数据集划分为若干个簇,进而令待分类数据集内具有较高相似度的簇互相分离[8-9]。该算法具有收敛性能良好、分类过程简便且速度较快的优势。K-means聚类算法的计算流程如图1所示。
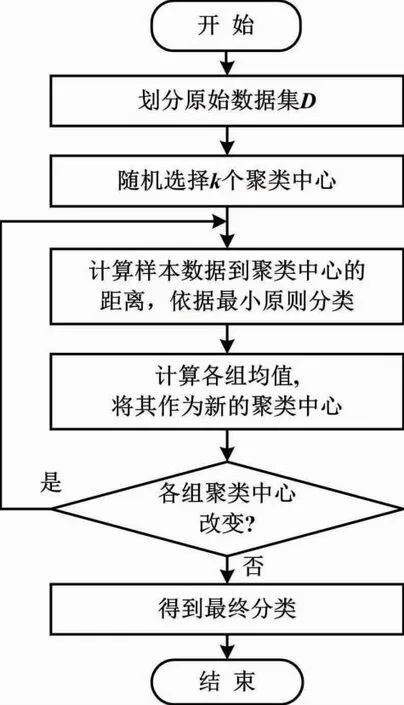
图1 K-means聚类算法的计算流程图
1.2 K值的选取
K-means聚类算法在计算时所使用的K值均是随机选取的。这会导致分类结果有所不同,存在一定的不稳定性。同时,对于不同场景和类型的数据而言,其分类结果也不尽相同。在应用中通常采用反推逆向法来解决这一问题。反推逆向法即根据不同的K值得出其相应的分类结果,并依据该结果选择最佳的K值。这种方法在绝大多数的应用中均能解决问题。然而,电力工程数据庞大且种类繁杂,使用此种方法不仅效率低下,而且效果不理想。
针对上述问题,本文提出了1种基于阈值判定的K值选取方法。在电力工程的各类数据中,同一类型、同一级别区域的数据均会集中在一定的范围内,因此可以给该范围内的数据设定1个距离阈值,并计算每个簇中的数据到该簇聚类中心的距离。若该距离小于设定的阈值,说明该聚类中心可以代表该簇;反之,则表示该聚类中心无法完全代表该簇,即K值选取不合理,需要重新选择。
K值选取的具体步骤如下。
①选取待分类电力工程数据集D′={l1,l2,…,lp-1,lp},并设聚类数值为K。
②计算任意2个样本间的空间距离d(li,lj)与每个样本聚类中心的空间距离d(lm,lk)。
(1)
式中:x和y为2个样本点的坐标;d(x,y)为两个样本点间的欧氏距离。
③计算任意2个样本间的平均空间距离d。
(2)
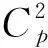
④计算当前数据集中的阈值q:
q=∑|d-d(li,lj)|
(3)
⑤比较所有d(lm,lk)及q的大小。当大多数的d(lm,lk)大于阈值时,说明当前聚类中心能够代表该簇,且K值的选择也是合理的;否则,K值加1,并重复步骤②~步骤④,直至满足条件。
1.3 属性加权优化空间距离算法
在常规的应用场景中,采用欧几里得式可计算出2个数据点的空间距离,进而衡量前2个数据间的关系。这种方法可行[10]。但随着电力系统中的能源种类越来越多,相关工程数据也愈加复杂。若仅依靠简单的欧几里得式,会导致电力数据的分类结果存在较大的偏差,难以正确体现出数据的真实特性。例如,在电力工程造价数据中就存在天气、地形、负荷需求等不确定因素。当数据点与簇中的聚集中心较远时,通过欧几里得式计算出的结果会存在距离过大以及相关性偏弱的问题。但实际上,该数据点与簇中心的相关性较强。针对上述问题,本文提出了1种属性加权优化空间距离算法,通过附加权重突出数据点与簇中心的相关性。以地形因素为例,其权重值Wp可定义为:
(4)
式中:D″为地形数据;g为地形系数,代表不同地形的情况,且地形越复杂,g值越大。
经过优化后的空间距离dij可以表示为:
(5)
通过给不同数据赋予不同的权重,可以突显出数据间的相关性。
2 数据预处理与评价指标
2.1 异常数据清理
电力系统的智能设备在采集数据时偶尔会出现故障,使得所采集的数据存在缺失、异常等问题,从而在对数据进行预测和处理时产生不良影响。因此,有必要对异常数据进行清理,即剔除重复性数据、利用差值法填充缺失数据,并对含有噪声的数据进行降噪和去噪处理。
2.2 数据归一化处理
电力工程数据的数量众多、类型繁杂且数值较大。为了提高算法的迭代速度并实现模型的快速收敛,需要对原始数据进行归一化处理,并将其缩小到(0,1]范围之内。本文采用最大最小值归一化式对数据进行处理。
(6)
式中:xr为经归一化处理后的数据;xmax、xmin分别为原始电力数据中的最大值与最小值。
2.3 评价指标
在数据分类中,通常采用准确率和容错率对算法的分类效果进行评价。本文也使用了这2个评价指标。
在数据分类完成之后,本文利用麻雀搜索算法(sparrow search algorithm,SSA)[11-12]优化了参数设置的LSTM神经网络,以实现对电力工程数据的预测功能。对于预测结果则采用平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)及决定系数(R2)进行评价。
(7)
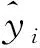
(8)
式中:RMSE为RMSE值。
(9)
3 算例分析
本文通过算例试验,验证所提改进K-means聚类算法是否能够快速、准确地对电力工程数据进行分类,并有效预测出相应的工程数据。算例分析试验所采用的数据集为澳大利亚某地区2017—2020年的相关真实数据。这些公开数据集记录了电力系统输电、配电等工程的历史造价、环境和评估指标。数据主要包括电压等级、土地面积、建筑工程、设备配置、生产过程、天气状况和地形条件等信息。
试验硬件平台为Intel Core i7-4500M CPU/16 GB RAM GPU/NVIDIA GT880M;软件平台为Windows 11操作系统常用的Jupyter Notebook编辑器。试验采用Python语言基于Tensorflow2.1 GPU进行算法搭建。
为了验证所提改进K-means聚类算法分类的有效性,本文将其与传统的K-means聚类、K-Medodis聚类、模糊聚类、NB分类以及KNN分类算法进行对比。为了避免随机性,每个聚类模型均进行20次的仿真试验。各算法的分类结果对比如表1所示。
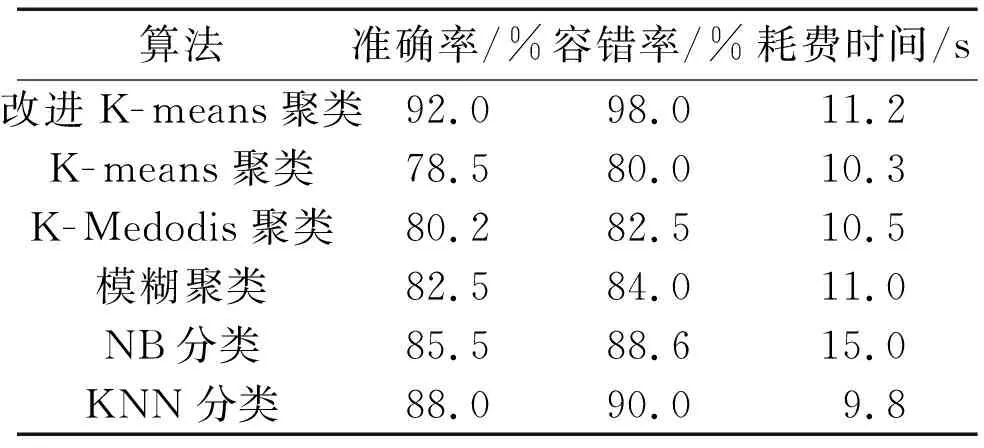
表1 各算法的分类结果对比
由表1可知,与传统K-means聚类算法相比,改进的K-means聚类算法准确性及容错率分别提高了13.5%及18%。其原因在于K值的选取对K-means聚类算法的分类结果会有较大影响。虽然改进后的算法在自动化选取K值时多花费了0.9 s,但整体耗费时间对运算的影响较小,故牺牲少量的时间成本来获得准确性更高的分类性能是值得的。综合对比,改进算法的分类效果在所有对比算法中最佳。
基于改进K-means聚类算法的数据分类结果,本文首先利用LSTM神经网络构建了工程数据的预测算法,然后利用SSA对LSTM神经网络的结构参数设置加以优化。为了验证所提SSA-LSTM算法能够满足实际的应用,本文将其与LSTM、遗传算法(genetic alginthm,GA)-LSTM、粒子群优化(particle swarm optimization,PSO)-LSTM及蝙蝠算法(bat algorithm,BA)-LSTM进行了对比测试。在本文所用造价数据集上进行的各算法的数据预测结果对比如表2所示。
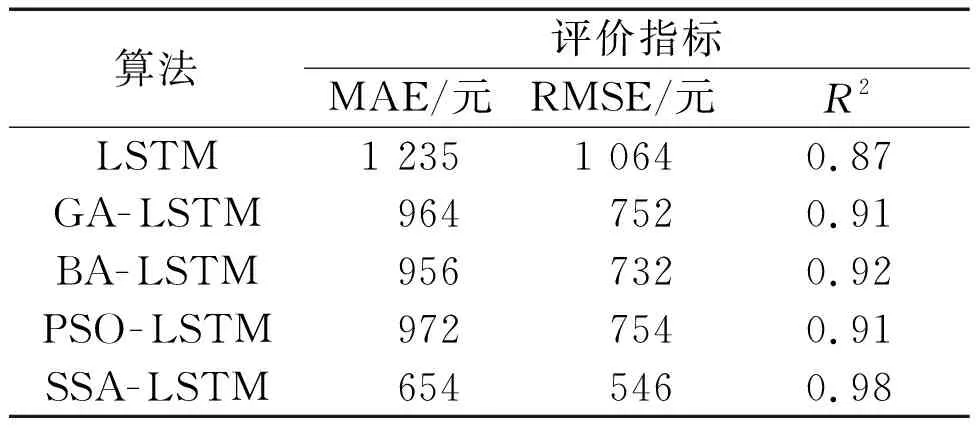
表2 各算法的数据预测结果对比
由表2可知,与常用的预测算法相比,所提SSA-LSTM算法的平均误差最小,RMSE与MAE至少分别降低了186元和302元,而R2则至少提高了6%。由此可得,所提SSA-LSTM算法可以快速、有效地实现电力工程数据的分类,且能够高精度、自动地预测出相关的工程数据。
4 结论
为了能够充分利用电力工程的信息数据库并得到高精度的工程数据预测结果,进而为电力工程的精细化管理提供数据支撑,本文设计了1种基于改进K-means聚类算法与LSTM神经网络的电力工程数据自动分类提取与分析技术。经过理论设计与测试分析可知,所提基于阈值判定的K值选取方法通过自动化选取最优K值,解决了传统K-means聚类算法因K值的不确定性而导致的最终分类结果不稳定的问题。本文采用属性加权的思想对空间距离的计算方法进行优化,通过对不同类型的数据赋予不同权重,突出簇中样本数据与聚类中心的相关性,进一步提高了分类算法的准确性及容错性。同时,本文还在高准确性分类结果的基础上,构建了基于SSA改进的LSTM工程造价预测算法。该算法对LSTM的参数结构进行优化后,预测精度得到了显著提高,能够满足目前对电力工程造价数据进行处理的需求。
后续研究可以在本文基础上增加超参数的数量和复杂度,以进一步提高预测精度。
