基于HySime 算法的端元个数估计

侯 璨，李志飞

（1. 上海飞未信息技术有限公司湖南分公司，湖南 长沙 410005；2. 湖南星图空间信息技术有限公司，湖南 长沙 410004）

高光谱遥感是用很窄而连续的光谱通道对地物持续遥感成像的技术。在可见光到短波红外波段其光谱分辨率高达纳米数量级，通常具有波段多的特点，光谱通道数多达数十甚至数百个以上，而且各光谱通道间往往是连续的[1]。目前高光谱遥感已经在自然资源、农业、林业等领域得到广泛应用，与高光谱有关的处理技术也迅猛发展。由于高光谱影像空间分辨率相对较低，在影像中普遍存在混合像元，混合像元的存在严重影响遥感分类和面积计算精度。为提高高光谱遥感应用的精度，首先需要解决混合像元分解的问题。混合像元分解的关键问题有2 个：①如何准确地估计端元的数目；②如何更有效地寻找出端元[2-3]。目前端元数目估计算法根据原理可以大致分为2 类：第①类是基于信息理论准则法，包括Akaike 信息准则（AIC，akaike’s information criterion）、最小描述长度（MDL, minimum description length）、贝叶斯信息准则（BIC,bayesian information criterion）等。第②类是基于特征值阈值法，常用的有HFC 算法（Harsanyi-Farrand-Chang）、噪声白化HFC 法（NWHFC,Noise whitened HFC）[4]、基于最小误差的高光谱信号识别算法（hyperspectral signal identification by minimum error，HySime）[5]等。AIC、MDL、BIC 算法都建立在似然函数对数的基础上，主要缺点之一是它们基于高斯噪声的假设。众所周知，高光谱遥感图像中的噪声一般不是高斯分布的。HFC、NWHFC 算法来源于涅曼皮尔森的探测理论，通过计算得到的相关特征值和协方差特征值分别表示由样本相关矩阵和样本协方差矩阵产生的特征值，HFC和NWHFC算法由于受误警率设置的影响，不同的误警率会导致不同的端元个数估计值。如何设定合适的误警率通常是算法的关键，基于高光谱数据的先验知识难以获取，因此我们很难确定合适的误警率。HySime 算法的自适应性强，不需要输入任何参数，因此广泛应用于估计端元个数。

本文采用HySime 算法对不同信噪比的高斯白噪声、高斯有色噪声模拟高光谱数据以及马蹄湾村真实高光谱数据的端元个数进行估计，科学评估算法的有效性、稳健性，为真实高光谱遥感影像端元个数估计提供参考依据。

1 HySime算法

HySime 算法首先是Bioucas-Dias 和Nascimento 提出来的，其基本原理是使用多元线性回归估计信号和噪声的相关矩阵。算法采用信号相关矩阵的特征向量子集来代替信号子空间，通过最小化投影误差功率之和与噪声功率来推断子空间，即通过增加或减少子空间的维数来估计端元个数。因此，如果子空间维数估计过高，噪声占支配因素；反之如果子空间维数估计过低，投影误差占支配因素。该算法的优点是计算效率高、非监督及全自动化。HySime算法主要包括噪声估计（Noise Estimation）和信号子空间估计（Signal Subspace Estimation）2个部分。

1.1 噪声估计

在数据分析特别是高光谱遥感数据处理中，噪声估计是一个常见的典型问题。移动差值法（Shift Difference）是最简单的噪声估计法，也被称为邻近像素差值法（nearest neighbor difference[6]，NND）。该方法首先假设邻近像素之间的噪声独立并且具有相同的统计量，同时其光谱信息也假定基本相同。为了获取有效的噪声估计值，移动差分法必须采用均质区域而不是整个影像区域。该方法存在2 种不足：①该方法假定邻近像素间有相同的信号信息，而在高光谱数据中该假设不一定满足；②为了改善噪声估计效果，必须采用监督方法选择均质区域。

HySime算法中噪声估计采用多重回归理论（multiple regression theory）。首先假设Y为N个L维光谱观测向量，定义Z=YT,zi=[Z]:,i，其中[Z]:,i为矩阵Z的第i列（zi为第i个波段的所有图像像素数据）。假定zi为其余L-1波段的线性组合，即

式中，Z∂i=[z1,…,zi-1,zi+1,…,zL] ∊RN×(L-1)；βi∊RL-1为回归向量；εi∊RN为模型误差；利用最小二乘法求得βi的估计值[7]：

噪声估计值为：

噪声相差矩阵。为了减小计算量，经过推导发现 可以通过去掉(ZTZ)-1的第i行、第i列后经过变换得到。具体算法如下：

1）输入高光谱数据Y=[y1,y2,…,yN] ；

2）令Z=YT,̂=ZTZ；

3）令；

4）for i=1:L

5）输出。

1.2 信号子空间估计

信号子空间估计是HySime 算法的核心。首先根据前节提到的噪声估计法确定信号空间的正交方向子集，然后通过寻找原始信号x和由y=x+n得到的x的噪声投影两者之间的最小均方根误差确定子集。假设噪声服从均值为零，协方差为的高斯分布，即。假定信号样本相关矩阵为，特征分解为：

式中，E=[e1,…,eL] 为的特征向量按特征值大小排列的特征向量矩阵。将空间RL分解为由Ek=[ei1,…,eik] 确定的k维子空间和由确定的子空间。假定为投影矩阵，经过推导可知子空间参数k的计算公式为[7]：

具体算法如下：

1）输入高光谱图像数据Y=[y1,y2,…,yN] ，并计算R̂y=(YYT)/N；

3）计算估计的信号相关矩阵；

4）计算；

5）计算k=argmin。

2 实验与结果分析

2.1 实验数据

为了更好地评价算法有效性，实验采用模拟数据和真实高光谱数据2种数据。模拟数据采用USGS光谱库[8]中明矾石、水铵长石、方解石、高岭石、云母5种光谱作为端元构建大小200×200 共224 个波段的模拟图像，光谱范围0.38～2.5 μm，光谱分辨率为10 nm ，其光谱曲线如图1所示。模拟图像的背影为5种光谱的均值，并构建25个模块，每一列的模块有相同的尺寸，如图2所示[9]。

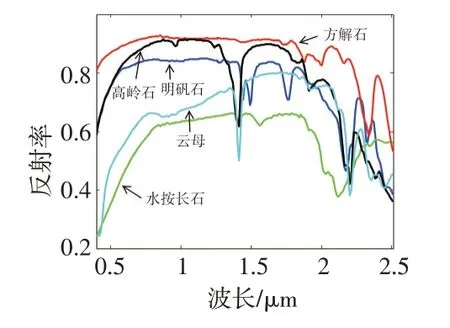
图1 5种光谱曲线

图2 25个模块

真实数据为雄安（马蹄湾村）高光谱数据集，该数据由中国科学院上海技术物理研究所研制的高分专项航空系统全谱段多模态成像光谱仪采集，光谱范围为400～1000 nm，波段数为256 个，影像大小为3750×1580，空间分辨率为0.5 m，数据的真彩色影像如图3所示。

图3 马蹄湾村高光谱数据真彩色影像

2.2 模拟数据实验结果及分析

考虑到算法的随机性，本次实验共分为5 组，每组实验采用HySime 算法分别对不同信噪比的高斯白噪声（η=0）和高斯有色噪声（η=1/18）高光谱影像进行端元个数估计，实验结果如图4所示。

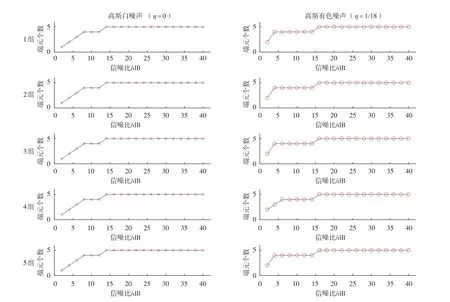
图4 模拟数据实验结果

采用HySime 算法估计高斯白噪声（η=0）高光谱模拟影像的端元个数，5 组实验估计端元个数的结果均相同，当信噪比SNR=2 dB时，估计端元个数为1；当信噪比SNR=4 dB时，估计端元个数为2；当信噪比SNR=6 dB 时，估计端元个数为3；当信噪比SNR=8、10、12 dB 时，估计端元个数为4；当信噪比SNR≥14 dB 时，估计端元个数为5。采用HySime 算法估计高斯有色噪声（η=1/18）高光谱模拟影像的端元个数，除第4组实验信噪比SNR=4 dB时估计的端元个数为3 外，其余估计的结果均相同，即当信噪比SNR=2 dB 时，估计端元个数为2；当信噪比SNR=4、6、8、10、12、14 dB 时，估计端元个数为4；当信噪比SNR≥16 dB时，估计端元个数为5。

综上所述，当信噪比SNR≥16 dB时,HySime算法能很好地估计法出端元个数，当信噪比低于16 dB时，HySime 算法估计的端元个数略低于实际端元个数。通过实验表明在高信噪比高光谱遥感数据中该算法可靠性高、稳定性好。

2.3 真实数据实验结果及分析

经过实地考察发现，该地区存在地物类别共计19 类，包括水稻茬、草地、榆树、白蜡、国槐、菜地、杨树、大豆、刺槐、水稻、水体、柳树、复叶槭、栾树、桃树、玉米、梨树、荷叶、建筑。为了科学评价HySime算法，本次实验分别采用HFC、NWHFC、HySime 算法对真实数据进行端元个数估计，并通过计算信号分量投影在信号子空间的相对功率来评价算法的精度，计算式为e=1-PE/PN，其中PE为信号分量投影在信号子空间的功率，PN为总功率。其端元估计的实验结果如表1所示，HySime算法的均方误差分布如图5所示。

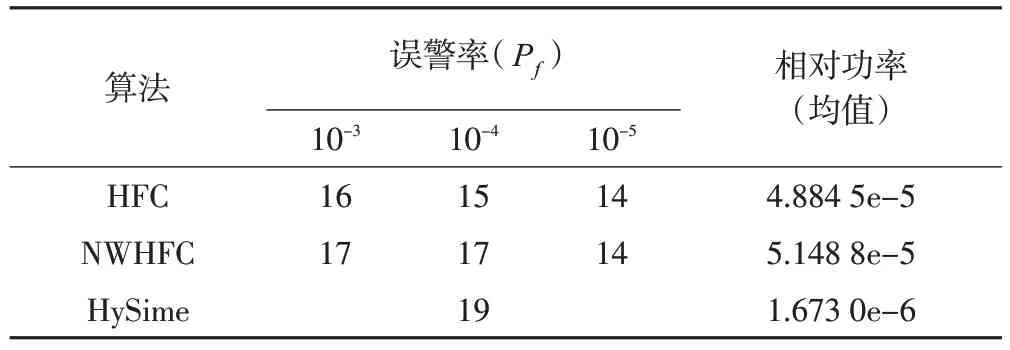
表1 雄安（马蹄湾村）数据端元个数估计结果

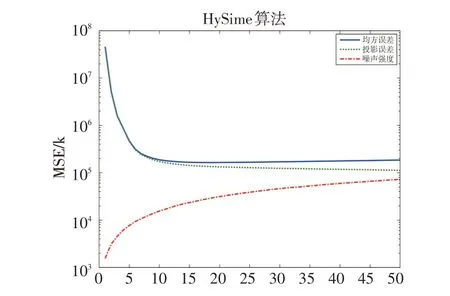
图5 端元个数估计均方误差分布图

在误警率为10-3条件下，HFC 和NWHFC 算法估算的端元个数分别为16、17；在误警率为10-4条件下，HFC 和NWHFC 算法估算的端元个数分别为15、17；在误警率为10-5条件下，HFC 和NWHFC 算法估算的端元个数均为14；通过表1的实验结果分析可知，HFC 和NWHFC 算法由于受误警率设置的影响，不同的误警率会导致不同的端元个数估计值。其整体趋势为正相关，即误警率越小，端元个数的估计值越少。而使用HySime 算法不受误警率设置影响，该实验所得的端元个数估计值为19。估算的端元个数与实地考察结果基本一致。通过相关学者的进一步研究发现，端元个数的差异会严重影响高光谱遥感影像地物分类精度，严重影响地物和光谱特征间的精确数量关系模型，在地物识别方面容易忽略微小地物等问题。

综上所述，由于HySime 算法适应性强，稳定性好，不需要输入任何参数等特点，通常采用此算法估算真实高光谱遥感影像估算端元个数。

3 结语

HySime算法首先使用多元回归估计信号和噪声相关矩阵，然后使用信号相关矩阵的特征向量子集来表示信号子空间。该子空间是通过最小化投影误差功率与噪声功率之和来推断的，它们分别是子空间维度的递减函数和递增函数。因此，如果子空间维度被高估，则噪声功率项占主导地位；如果子空间维度被低估，则投影误差功率项占主导地位。通过一系列模拟数据及真实高光谱数据进行的实验结果表明该算法自适应性强，稳定性好，不需要输入任何参数，是一种准确估计高光谱影像的端元个数的算法。通过相关学者对HySime 算法进一步的研究，我们可以了解Hy-Sime算法对弱端元的探测能力较差，算法过程中容易忽略弱端元。但是，由于高光谱数据的空间分辨率较低，采用高光谱数据通常是基于宏观上的分析研究，而忽视弱端元的存在对精度影响较小，基本能够满足需求，因此在端元个数不清楚的地区通常使用此算法估计端元的个数。