基于改进粒子群的配网多无人机灾损巡检任务分配方法

胡振维 莫一夫 李 钰 郑松源 潘岐深

（广东电网有限责任公司）

0 引言

随着我国经济快速发展，配电网规模不断扩大，覆盖范围逐渐扩展至城市及农村地区。传统的巡线方式已难以满足配电网设备的巡检需求，其存在效率低、巡检周期长等问题。因此，借助现代化的无人机技术进行配电网巡检成为一种具有广阔前景的选择［1］。无人机具有高效、灵活、全面的特点，可大幅提高配电网巡检效率，减少人力资源投入，并能够覆盖更广泛的区域，在这一背景下，如何合理地利用多架无人机进行配电网巡检成为迫切需要解决的问题［2］。目前，众多研究者关注如何根据电网设备的分布情况、巡检区域的特点、无人机的属性等因素，通过优化算法来实现任务的合理分配和调度，从而最大程度地提高巡检效率和覆盖范围［3］。同时，还有一些研究致力于利用人工智能技术，如深度学习和强化学习，对无人机巡检数据进行高效处理和分析，进一步提升无人机巡检的智能化水平。在该背景下，本次研究开展基于改进粒子群的配网多无人机灾损巡检任务分配方法设计研究。

1 构建配网多无人机灾损巡检任务分配模型

在进行配电网灾损任务巡查时，其巡查目标常分布于不同地点、不同高度，故常常需要配备一个高空无人机和低空无人机一同进行巡查任务，以提升任务巡查的成功率。在配电网灾损巡检时，其协同任务的分配主要受到五个因素影响，可对其表示为｛E，V，T，M，P｝。其中E表示配电网巡检任务环境，假定无人机群在三维环境E中执行任务，三维环境包含三要素｛x，y，z｝，因此在t时刻编号为i的无人机地理位置坐标可表示为｛xi（t），yi（t），zi（t）｝［4］。设Vi为给定的一个无人机群，Nv为给定无人机群中无人机的数量。其中，这Nv架无人机中有Ns架低空无人机和M架高空无人机，即有Vi(Vi∊V,i=1,2…,NS)和Vi(Vi∊V,i=NS+1,…,NV)，且存在NS+NM=NV［5］。将多个巡检任务目标设为Ti，其中任务数大于无人机数可表示为NT>NV。MT表示无人机群需要执行的任务类型，Ktype为任务类型数，若每个目标Ti上都有Ktype种类型，则总共有Ti⋅Ktyре个任务。每架无人机都有一个任务集合，其可表示为Si={Ti1,…,Tin}，则所有任务分配可以描述为：在输电线路灾损巡检环境中进行多无人机任务分配目标函数设计时，需要考虑以下几个因素：第一，无人机与线路中巡检目标的空间位置关系；第二，多巡检无人机在完成任务时的定位关系；第三，无人机巡检时的飞行时间；第四，无人机灾损巡检的作业成功率［6］。

本次设计的多无人机灾损巡检任务分配目标函数主要由代价函数构成，其可表示为：

式中，JCost为代价函数；a1代表加权系数［7］。其代价函数主要由航程代价、时间代价和无人机损耗代价构成，可表示为：

式中，Jpath为航程代价；Jtime为时间代价；JRisk为无人机损耗代价；C1，C2，C3均为大于0小于1的常数，大小由决策者决定，其可反映各个目标函数的重要程度及指挥决策人员事先确定的倾向性选择，且其参数间存在C1+C2+C3=1。

综上，完成其目标函数整理，其可表示为：

接下来，对其约束条件进行分析，其分别为：

1）每架低空巡检无人机必定配有一架无人机用于监控，则有：

2）对于各个待巡检目标而言，其每个任务都只能完成一次，则有：

2）每架巡检无人机从TStart时刻开始，最多访问巡检节点一次，其可表示为：

3）无人机飞行时间最长tmax，则每架无人机任务执行期间时间不得超过最长飞行时间，其可表示为：

综上，完成配网多无人机灾损巡检任务分配模型构建。

2 基于改进粒子群的任务分配模型求解

在完成配网多无人机灾损巡检任务分配模型构建后，为获得模型最优解，避免模型求解陷入局部最优，本次采用粒子群算法完成求解。粒子群算法是一种常用的群集智能搜索方法，其通过模仿鸟类的行为，在一个特定的空间中搜索最优解。在传统粒子群算法中，由于其对参数配置及搜索空间的处理方式较为简单，难以在复杂的多目标、约束条件等问题上获得较好的效果，故本次对其进行改进，以提升其泛化能力，获得任务分配模型的最优解。应用改进后的粒子群优化算法进行求解的步骤如下所示：

1）先建立粒子群，并完成其群体的初始化，对粒子检索速度、位置和最大迭代数进行设置，然后将学习因子设置为c1，c2，惯性权重设置为ω；

2）对现有群体中各个粒子的位置进行求解，并判断其是否满足约束条件；如满足则直接输出；如不满足，则利用粒子进行检索，更新粒子位置；

3）计算各个粒子的适应度值，保存每个粒子所能达到的最优位置和适应度值。

4）完成粒子惯性权重的更新，并调整两个学习因子，利用下式完成群体中粒子速度和位置的更新，其可表示为：

式中，d表示区域空间维度，Vid为粒子速度，Xid（k）为粒子位置，c1，c2为学习因子，r1，r2为［0，1］区间内两个随机正数，Pid为粒子个体的位置最优解，Pgd为粒子群体的位置最优解。

5）搜索粒子群中适应度最佳个体的最优位置和适应度值，判断其优于上次检索，如满足则直接替换，如不满足则持续检索。

6）判断当前算法迭代次数是否满足要求，如满足则直接输出最优群体中最佳粒子个体的最优位置，其即为最佳目标分配方案；如不满足，则跳转至步骤3，继续搜索。

通过上述，将输出带入目标函数中，完成任务分配模型求解，实现配网多无人机灾损巡检任务分配功能。

3 实验与分析

为验证所提方法的先进性，选择了一条输电线路作为研究对象，并获得了线路环境等数据，以便后续进行测试。首先，将利用MATLAB软件搭建仿真模型，设置任务分配区域大小为100×100，然后模拟由2架MUAV监控下的4架SUAV执行8个任务的动态分配情况，通过编号为S-1、S-2、S-3和S-4的SUAV执行这些任务，其三维坐标分别为：（10，70，35），（20，80，35），（15，20，30），（25，10，35）；2架MUAV中编号为M1的三维坐标分别为（50，80，60）；M-2的三维坐标分别为（45，30，75），其任务坐标分别为：（45，55，15），（65，75，10），（65，35，20），（75，25，10），（75，45，15），（73，68，15），（30，35，20），（80，65，20），以此为基础，采用所提方法进行配网多无人机灾损巡检任务分配，并将其效果与未应用前规划效果相比较，得到对比结果如下图1所示：

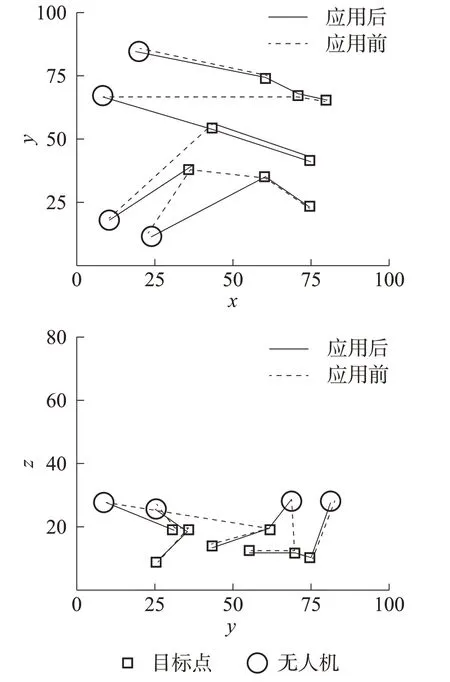
图1 任务分配结果

如图1所示，应用所提方法后，在两架MUAV的监控下，待执行的任务被有序地分配给了SUAV编队，而未应用所提方法时，其规划效果较差，存在无人机反复巡检的过程，应用效果较差，验证此时应用所提方法设计的任务分配方案应用效果较好。

4 结束语

本次研究提出的基于改进粒子群的配网多无人机灾损巡检任务分配方法在提高任务分配效果方面有一定的潜力。该方法通过充分考虑任务环境、无人机群和巡检任务目标等因素构建任务分配模型，并应用改进粒子群算法进行求解，实现了避免无人机反复巡检的优化效果，应用效果较好。