R语言实例解析肿瘤治疗药物经济学评价的分区生存模型

刘家一，李 伟

1.中国人民大学公共管理学院（北京 100872）

2.北京医院麻醉科（北京 100005）

分区生存模型（partitioned survival model，PSM ） 是国外肿瘤治疗药物经济学（pharmacoeconomics，PE）评价中应用较多的一种决策模型，用于肿瘤药物的报销决定[1-2]。PSM已在英国国家卓越健康与护理研究所（National Institute for Health and Care Excellence，NICE） 技术评估（Technology Appraisal，TA）计划和加拿大药物与卫生技术局（Canadian Agency for Drugs and Technologies in Health，CADTH）评价中广泛使用，是目前NICE 评估晚期或转移性癌症干预措施的最常用方法[1,3]。与国内研究者常用的状态转移模型相比，PSM 具有简洁、直观的特点，它直接利用肿瘤治疗药物临床报告中的无进展生存期（progression free survival，PFS）、总生存期（overall survival，OS）数据，避免在数据有限的情况下计算并验证复杂的状态间转移概率[4-8]。

在PSM 应用中，尽管TreeAge 等软件在建模方面具有一定优势，但其固有设置要求定义状态间转移概率，限制了其在PSM 中的应用[9]。相较之下，R 语言在药物成本效用分析中灵活性更强，专用程序包可直接应用PSM，同时提供了丰富的数据处理与可视化功能。国际研究者已在不断尝试和探索新的模型结构和变量选择方法过程中产生了不同功能的专用程序包，如健康经济模型分析的heemod[10-11]、提供灵活生存分析方法的flexsurv[12]、集成了健康经济模型模拟分析的hesim[13]、标准生存数据分析的survival[14]、结合了生存分析与健康经济评估的survHE[15-16]、执行贝叶斯成本效益分析的BCEA[17]等。利用R 语言进行肿瘤治疗药物的PSM 分析，能够快速、直观地复现结果，在缺乏患者个体数据（individual patient data，IPD）的情况下，研究者可直接提取临床试验报告中公开的PFS、OS 曲线数据[13,18]，以重新构建IPD 并完成整个PE 评价，但这要求研究者具有数理统计、健康经济分析与编程的综合知识背景，国内采用R 语言进行PSM 分析的应用报道不多，且缺乏具体实施案例。本研究以帕博利珠单抗治疗非小细胞肺癌（non-small cell lung cancer，NSCLC）的 KEYNOTE189 临床试验（简称KN189）[19-20]为例，实现从数字化提取PFS、OS 曲线数据，然后由R 语言实现PE 分析与评价的全过程，以期为研究人员利用R 语言进行PE评价提供参考。

1 临床试验数据提取

基于帕博利珠单抗Pembrolizumab KN189临床试验数据[19-20]（图1、图2），使用GetDataW 2.26.0.20 软件分别对其OS、PFS 曲线数据进行提取，同时提取number at risk 数据，一并保存为xlsx 文件。针对提取后数据进行整理，使后一个时间点的生存率小于或等于前一个时间点数值。

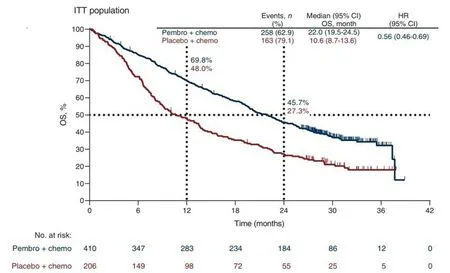
图1 KN189临床试验OS曲线数据Figure 1.OS curve data of KN189

图2 KN189临床试验PFS曲线数据Figure 2.PFS curve data of KN189

2 重构IPD

2.1 R语言环境设置

打开Rstudio 2023.09.1+494 软件，设定工作路径，安装并下载软件包：survial（v 3.5-7）、survHE（v 2.0.1）、IPDfromKM（v 0.1.10）、readbitmap（v 0.1.5）、survminer（v 0.4.9）、flexsurv（v 2.2.2）、data.table（v 1.15.2）、hesim （v 0.5.4）、openxlsx（v 4.25.2）。

2.2 定义数据集

基于KN189 试验方案，将对照组命名为cemo，帕博利珠组定义为comb，OS 曲线命名为surv，PFS 曲线命名为pfs。分别通过read.xlsx()函数读取第1 步中提取的xlsx 文件，整理并保存为如下数据集：survcomb、survcemo、nriskcomb、nriskcemo、pfscomb、pfscemo、nsirkcomb，表1、表 2分别展示了survcomb 与nriskcemo 数据集的数据结构。此处仅示例OS 曲线的数据重构过程，PFS 曲线与OS 曲线的数据提取过程类似。

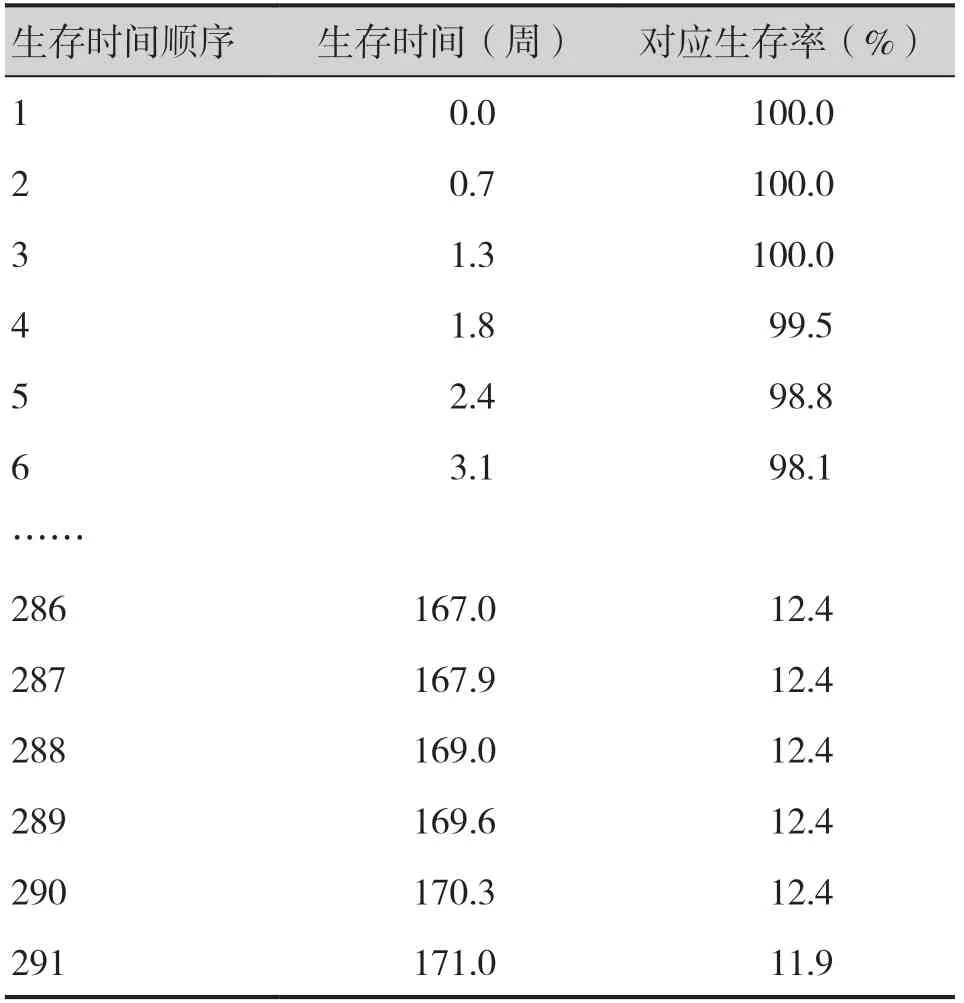
表1 KN189试验comb组OS曲线数据Table 1.OS curve data of the comb group in KN189

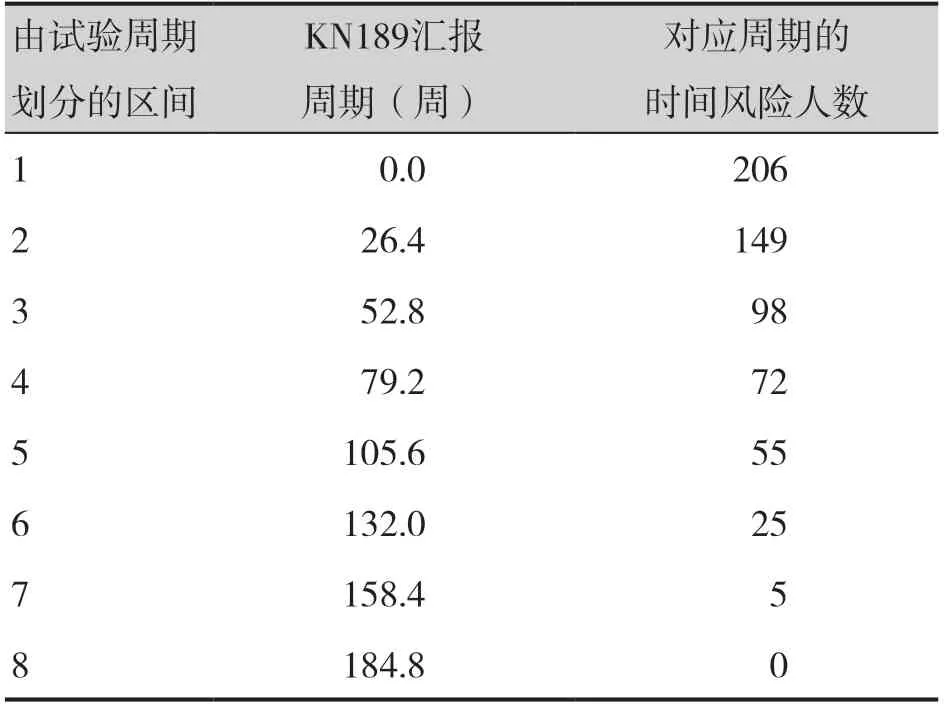
表2 KN189试验cemo组OS曲线风险人数数据Table 2.OS curve data of the cemo group in KN189

2.3 预处理与重构IPD数据

2.3.1 预处理IPD对象格式

使用preprocess()函数预处理为IPD 对象适当格式，R 语言代码如下：

pre_comb＜- preprocess (dat=survcomb,trisk=nriskcomb$time, nrisk=nriskcomb$nrisk,totalpts=410)

totalpts 为指定试验的初始人数；

pre_cemo＜- preprocess (dat=survcemo,risk=nriskcemo$time, nrisk=nriskcemo$nrisk,totalpts=206)

206 为cemo 组试验的初始人数。

2.3.2 重构IPD数据

使用getIPD 函数重建comb 组OS 曲线IPD数据，运行代码如下：

est_comb＜ getIPD (prep=pre_comb, armID=1,tot.event=NULL)

summary (est_comb)

查看est_comb 数据集可知，采用IPDfromKM包的Kolmogorov_Smirnov(K-S) Test，得到D 值为0.053，p_value 为0.99，预测值est_comb 与read _in的临床数据pre_comb 数据无显著性差异，可进行后续分析，代码如下：

est_cemo＜-getIPD (prep=pre_cemo, armID=2,tot.event=NULL)

同理获得cemo 组OS 曲线IPD 数据，armID定义为2。

2.3.3 对比重构IPD数据与KN189的HR值

重构IPD 数据与KN189 报告的风险比（hazard ratio，HR）值对比分析的R 语言运行代码如下：

est_IPD_comb_cemo＜-rbind (est_comb$IPD,est_cemo$IPD)

提取comb、cemo 组的重构IPD 为新数据集；

hr_est_IPD＜-coxph (Surv(time,status)～treat,data=est_IPD_comb_cemo)

计算重构IPD数据中comb、cemo组的HR值；

exp (coef (hr_est_IPD)

运行并提取HR 值为0.57，与KN189 报告中数值0.56 相近。

2.4 绘制重构IPD数据与原read_in曲线对比检验

使用plot 绘制comb 组与cemo 组重构IPD 数据与read_in 的临床数据比较图，图3 显示两组数据重合度较高。若重构IPD 与read_in 曲线对比图可见明显差异，则需从第1 步开始重复以上开始步骤，并检查原始数据，具体代码如下：

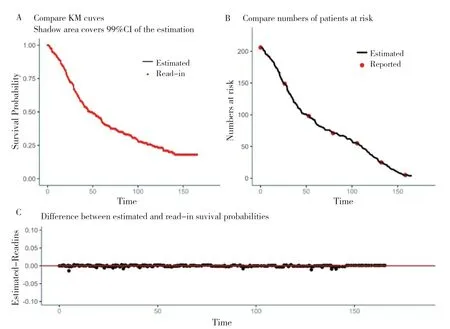
图3 cemo组重构IPD数据OS曲线与read-in KN189数据OS曲线对比Figure 3.Comparison of OS curves of reconstructed IPD data and read-in KN189 data in cemo group

plot(est_comb)

Estimated 为重构IPD 数据，Reported 为read_in KN189 临床数据；

plot(est_cemo)

如图3 所示，图3-A 为基于重构IPD 数据的OS 曲线与数字化读取的KN189 临床试验的OS 曲线的视觉对比图。

将两组IPD 数据分别加上treat 列并分别赋值为1、2，然后将comb 与cemo 组的重构IPD 数据整合为数据框（表3），具体代码如下：

表3 OS曲线重构IPD数据Table 3.Reconstructed IPD data of OS curve

IPD_comb_cemo_os

surcombIPD＜- transform (est_comb$IPD,treat=1)

将治疗方案comb 组定义为1；

surcemoIPD＜- transform (est_cemo$IPD,treat=2)

将治疗方案cemo 组定义为2；

IPD_comb_cemo_os＜- rbind (surcombIPD,surcemoIPD)

重复以上2.2 至2.4 步骤，得到OS 曲线的重构数据框IPD_comb_cemo_os。

3 生存曲线参数分布拟合与评估

定义待拟合模型名称的向量，同时考虑指数、威布尔、伽玛、对数正态、对数逻辑及广义伽玛多个模型，运行代码如下：

mods1＜-c (＂exponential＂, ＂weibull＂, ＂gamma＂,＂lognormal＂, ＂loglogistic＂, ＂gengamma＂)

定义模型公式，采用Surv()函数，以数据框中分类变量treat 作为协变量分析，具体代码如下：

formula＜- Surv (time, status)～ as.factor (treat)

执行批量生存模型分析，采用最大似然估计（maximum likelihood estimates，MLE），使 用flexsurv 包fit.models()函数创建survHE 对象KN189case_mle，其中存储了所考虑的多个参数模型的拟合结果，代码如下：

KN189case_mle＜-fit.models (formula=formula,data=IPD_comb_cemo_os, distr=modsl, method=＂mle＂)

KN189case_mle$model.fitting

显示批量拟合的结果AIC、BIC、DIC 值。

基于AIC、BIC 较小者模型拟合佳的原则，本例结果显示AIC、BIC 值最小的拟合为loglogistic，即loglogistic 模型拟合度最优。同样步骤进行MLE 批量拟合IPD_comb_cemo_pfs，结果也显示loglogistic 拟合模型的AIC、BIC 值最小，拟合度最优。

4 构建生存、效用、费用模型

4.1 定义模型

调用R 软件hesim 包的hesim_data 函数[13]，用以标准化后续生存效用模型的数据准备，代码如下：

hesim_dat＜- hesim_data (strategies =data.table (strategy_id=1 : 2, strategy_name=c (＂comb＂,＂cemo＂))，

patients=data.table (patient_id=1, grp_id=1),states =data.table (state_id=1 : 2, state_name=c(＂Stable＂, ＂Progression＂)))

分别定义分区生存模型中治疗方案strategies、患者类型patients、试验疾病状态states，死亡状态不用列出。

labs＜- get_label (hesim_dat)

4.2 建立生存模型

将IPD_comb_cemo_os、IPD_comb_cemo_pfs数据合并，并整理为数据框surv_est_data，整理后的数据结构见表4。

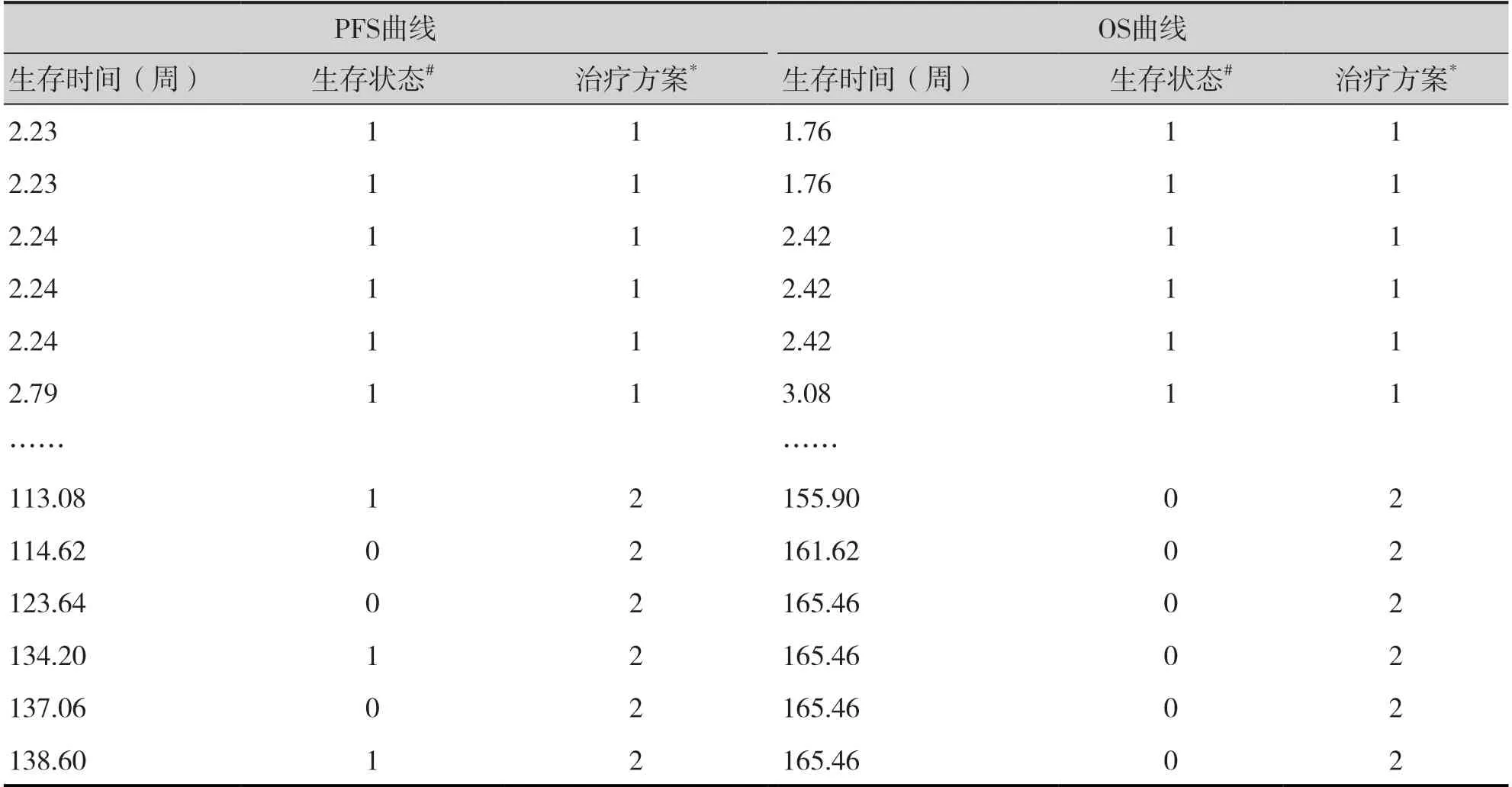
表4 comb与cemo组OS及PFS曲线的重构患者数据Table 4.Reconstructed patient data of OS and PFS curves in comb group and cemo group

采用flessurvreg()函数，基于重构IPD 数据集surv_est_data，分别拟合OS 及PFS 生存模型，代码如下：

flex_fit_os＜- flexsurvreg (Surv (os_time, os_status) ～strategy_name, data=surv_est_data,dist=“llogis”)

选择步骤3 中pfs 及os 曲线最优拟合模型llogis：

flex_fit_pfs＜- flexsurvreg (Surv(pfs_time, pfs_status)～strategy_name, data=susurv_est_data,dist=＂llogis＂)

综合flex_fit_os 及flex_fit_pfs 模型为psfit_wei，代码如下：

psfit_wei＜- flexsurvreg_list (flex_fit_pfs, flex_fit_os)

包含了3 个状态分别的生存拟合结果对象。

建立生存模型survmods，调用hesim 程序包的create_PsmCurves()函数。在其参数设定中，明确boostrap 为确定生成结果不确定性的方法，n为boostrap 的样本数，运行代码如下：

n_samples＜- 300

设定生存模型中将要模拟的样本数量；

surv_input_data＜- expand(hesim_dat,by=c(＂strategies＂, ＂patients＂）

从hesim_dat 中指定参数进行模拟；

survmods＜- create_PsmCurves (psfit_wei, n=n_samples, input_data=surv_input_data,

uncertainty=＂bootstrap＂, est_data=＂surv_est_data＂)

input_data: hesim 数据框架，包含了需要生成生存函数的所有患者和策略组合形式；n 为用于bootstrap 的样本数；uncertainty 用于确定生成结果的不确定性的方法，本例使用bootstrap 方法；est_data: hesim 数据集，类似于IPD 生存状态与时间数据及其他如年龄等所有额外信息。

4.3 建立效用模型

疾病状态的效用值采用文献数据[21]，即pfs=0.815、pd=0.321，其效用值参数的变化范围：DSA 在+15%范围，PSA 为beta 分布。据此定义状态效用值数据框（表5），运行代码如下：

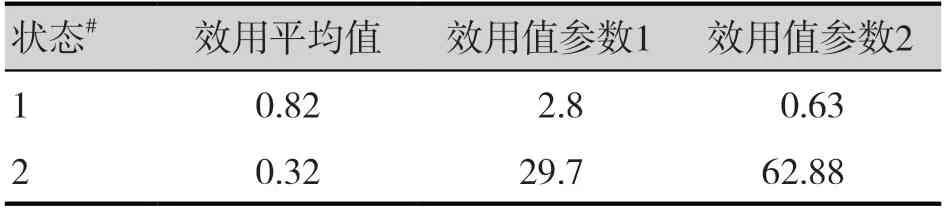
表5 不同状态效用值Table 5.Utility values for different states

utility_tbl＜- stateval_tbl (utility_data,dist=＂beta＂)

utilitymod＜- create_StateVals (utility_tbl, n=n_samples, hesim_data=hesim_dat)

4.4 建立费用模型

根据KN189 临床设计方案，针对使用药品费用（包括疾病进展后使用二线治疗方案药物、不同方案治疗比例）、检查检验的周期计划及费用、不良反应发生率及相应治疗费用、临终关怀费用等，采用药智网及北京市医疗费用收费标准进行综合计算，得出comb、cemo 组各自总体费用的均值（表6），运行代码如下：

表6 不同治疗方案费用Table 6.The cost of different plans

cost_strategy_id

cost_tbl＜- stateval_tbl (cost_strategy_id,dist=＂fixed＂)

costmod＜- create_StateVals (cost_tbl, n=n_samples, hesim_data=hesim_dat)

5 实例化PSM并计算质量调整生命年

5.1 定义模型

生存模型survmods 与后续的效用模型、费用模型汇总进行PSM 的实例化，并进行时间外推，分析代码如下：

psm＜- Psm$new (survival_models=survmods,utility_model=utilitymod, cost_models=list(medical=costmod))

times＜- seq (0, 1000, by=50)

定义生存模型实例化外推时间的范围为20年，与前数据统一以周为单位，将时间范围带入psm 进行生存预测；

psm$sim_survival (t=times)

将定义的外推时间输入psm 进行生存预测。

5.2 绘制外推生存曲线图

基于以上所定义的外推时间范围times 内，将实例化PSM 中的生存概率绘制生存曲线，结果见图4，分析代码如下：

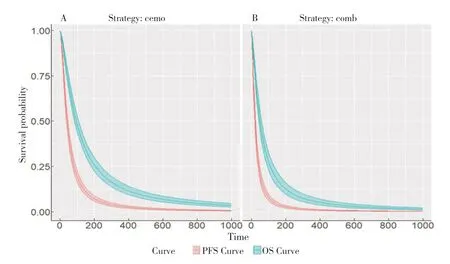
图4 外推时间内的PFS和OS曲线Figure 4.PFS and OS curves over time

labs$curve＜- c(＂PSF_Curve＂=1, ＂OS_Curve＂=2)

autoplot (psm$survival_, lables=labs, ci=TRUE,ci_style=＂ribbon＂,

scale_x_continuous (breaks=seq (o, max (times), 50))

psm$sim_stateprobs()

整理状态概率数据框，用于后续视图表现；

stateprobs＜-psm$stateprobs_[sample==2&patient_id==1]

从psm 对象中任选一个子集，选择sample=2且patient_id=1，将其状态概率定义给到stateprobs；

stateprobs [, state: =factor (state_id, state,levels=rev (unique (state_id)))]

在stateprobs 数据框中增加state 列，将state_id 转换为因子类型的变量赋值给state 列，并指定其级别为唯一值且逆序排列；同理增加strategy 列如下：

stateprobs [, strategy: =factor(strategy_id,labels=c (hesim_dat$strategies$srategy_name))]

基于整理的stareprobs 绘制状态概率曲线，见图5，分析代码如下：

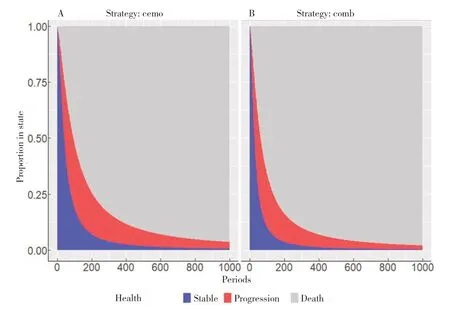
图5 外推时间内的状态曲线Figure 5.State curves over time

ggplot (stateprobs [strategy_id % in% c (1 : 2)]

指定数据来源stateprobs 中strategy_id 列数据绘图；

aes(x=t, y=prob, fill=state, group=state))+

定义x、y 轴分，根据state 列不同值着色分组；

geom_area (alpha-.65), facet_wrap(～strategy)

将图形分面，每个分面表示不同的策略(strategy)；

abs (x=＂Periods＂, y=＂Proportion in state＂)

设定x、y 轴的文字标识；

scale_fill_manual (name=＂Health state＂

设置图例的标题；

values=c(＂gray＂, ＂red＂, ＂blue＂)

设置填充图形的颜色映射；

lables=c (＂Death＂, rev (hesim_dat$states$stat e_name)))+

标识每个状态的文字内容；

scale_x_continuous (breaks=seq(0, max(times), 50)+

设置x 轴的刻度标签；

guides (fill= guide_legend (reverse=T, nrow=2,byrow=TRUE))+

调整图例以逆序的方式且排2 行；

theme (legend.position=＂bottom＂)

设置图例的位置在底部。

5.3 模拟成本与质量调整生命年

基于5.2 中的状态概率进行数值积分模拟贴现成本与质量调整生命年（quality-adjusted life years，QALYs），选择5%进行贴现，分析代码如下：

psm$sim_costs (dr=0.05)

运行后结果见图6。

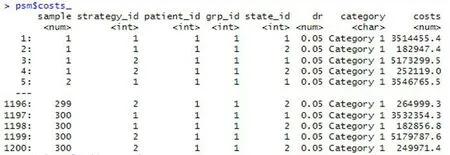
图6 基于PSM以5%的折现率模拟的贴现成本Figure 6.Discounted cost simulated based on PSM at a 5% discount rate

psm$sims_qalys (dr=0.05)

运行后结果见图7。

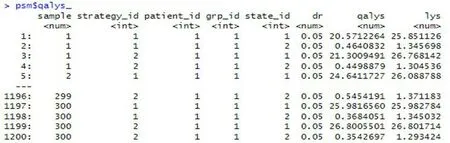
图7 基于PSM以5%的折现率模拟的贴现效用Figure 7.Discounted utilities simulated based on PSM at a 5% discount rate

6 视图辅助决策的成本效用分析

6.1 创建模拟数据

调用hesim 包的cea()和cea_pw()函数分别执行单一或成对的两种治疗策略的成本效益分析，其运行结果对象中包含有每个PSA 样本的平均成本与QALYs。先用summarize()方法创建一个具有平均值的hesim::ce 对象，并将其赋值给变量ce_ sim，该对象包括了在概率敏感分析PSA 中使用的模拟结果的摘要统计信息，分析代码如下：

ce_sim＜- psm$summarize()

wtp＜- seq (from=0, to=20 000, by=2 000)

定义支付意愿阈值wtp 的范围，以此进行CUA 分析；

cea_out＜- cea (ce_sim, dr_qalys=.05,dr_ costs=.05, k=wtp)

将cea()函数分析结果赋值给变量cea_out；

cea_pw_out＜- cea_pw (ce_sim, comparator=1,dr_qalys=.05, dr_costs=.05, k=wtp)

cea_pw()函数计算人群加权增量成本-效果比（populattion-weighted incremental costeffectiveness ratio，PWICER），comparator=2 即将strategy_id=2 的cemo 组为基准策略分析偏好权重，K 为支付意愿阈值。

6.2 绘制成本效果可接受曲线

从cea_out 中提取strategy_id=1 的comb 组成本效果数据，并绘制单组的成本效果可接受曲线，分析代码如下：

strategy_1_data＜- cea_out$mce [strategy_id==1]

cea_ac_plot＜- ggplot (data=strategy_1_data,aes(x=strategy_1_data$k, y=strategy_1_data$prob,group=1))+

geom_line (linewidth=1), xlab (＂k＂)+ylab(＂prob＂)+

ggtitle (＂Cost-Effectiveness Acceptability Curve＂), theme_minimal()

提取strategy_id=2 的cemo 组数据，将两组数据合并后，同时绘制cemo 与comb 组的成本效果可接受曲线：

strategy_2_data＜- cea_out$mce [strategy_id==2]

combined_data＜- rbind (strategy_1_data,strategy_2_data)

colors＜- c (＂blue＂, ＂red＂)

labels＜- c (＂Strategy 1＂, ＂Strategy 2＂)

cea_ac_plot＜- ggplot (data=combined_data, aes(x=k, y=prob, color=factor (strategy_id))) +

geom_line (linewidth=1), xlab (＂Willingness to pay＂) , ylab (＂Probability Acceptable＂)+

scale_color_manual (values=colors,lables=lables),

guides (color=guide_legend (title=＂Strategy＂))+

ggtitle (＂Cost-Effectiveness Acceptability Curve＂), theme_minimal()

print(cea_ac_plot)

由图8 可知，当支付意愿值超过4 800 元时，comb 组具有成本效益的可能性开始大于cemo 组。

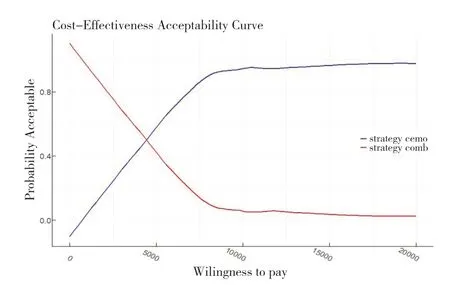
图8 comb组与cemo组成本效果可接受曲线Figure 8.Acceptable cost-effectiveness curves of the comb group and the cemo group

6.3 绘制增量成本-效益比值散点图

绘制增量成本-效益比值（incremental costeffectiveness ratio，ICER）散点图，设定支付意愿值上下限并在图中添加97.5%和2.5%可能性的正比例函数线条，运行代码如下：

strategy_1＜- cea_pw_out$delta [strategy_id==1, ]

提取cea_pw_out 数据集中comb 组的数据；

startegy_1$icer＜- strategy_1$ic/strategy_1$ie

计算comb 组的ICER；

wtp_2＜- quantile (strategy_1$icer, probs=0.975)

wtp_3＜- quantile (strategy_1$icer, probs=0.025)

cea_sensitivity_plot＜- ggplot (data=cea_pw_out$delta,

aes (x=ie, y=ic, color=strategy_id, size=3,alpha=0.8))+

geom_point (color=＂red＂, size=3, alpha=0.8)+

geom_abline (slope=wtp_2, intercept=0,color=＂blue＂, linetype=＂dashed＂)+

geom_abline (slope=wtp_3, intercept=0,color=＂red＂, linetype=＂dashed＂)+

geom_text (data=data.frame (x=0.2, y=3 000,lable=paste0 (＂97.5% ICER=＂, round (wtp_2,2))) ,

geom_text (data=data.frame (x=1.8, y=3 000,lable=paste0 (＂2.5%ICER=＂, round (wtp_3,2))),

xlab(＂Incremental Effectiveness＂),ylab(＂Incremental Cost＂)+

ggtitle (＂Sensitivity Analysis＂), xlim (0, 1.25),ylim (1650000, 1800000)+

theme_minimal()

print (cea_sensitivity_plot)

由图9 可知，当意愿支付阈值为14 312 时，comb 组干预方案具有成本-效益的可能性为97.5%；当意愿支付阈值为3 123 时，comb 组干预方案具有成本-效益的可能性仅为2.5%。

图9 comb组Bootstrap自助法抽样300次后得到的ICER散点图Figure 9.Scatter plot of ICER obtained after 300 iterations of Bootstrap resampling in the comb group

7 讨论

本研究展示了R 语言在成本效用分析中的高效性，具体表现在：一是代码透明性，分析过程完全通过代码记录，确保模型运行的透明性；二是计算可重复性，仅需重新运行代码即可重复整个计算过程并更新结果；三是错误识别与调整便捷性，模型设计及参数设定的错误或假设调整易于发现与更正；四是结果输出直接性，PE 评价结果可直接通过R 代码生成；五是敏感分析，可通过扩大分析的范围评估关键参数和假设变化对模型输出的影响，从而捕捉不确定性、识别关键参数及优化模型；六是结果输出直接性，PE 评价结果可直接通过R 代码生成。此外，还具有模型的灵活性，hesim 程序包[13]为健康经济学模拟提供了一个灵活的框架，除PSM 外，还提供马尔科夫模型（Markov models）、状态转换模型（state- transition models，STM）、队列状态转换模型（cohort state-transition models）和个体状态转换模型（individual state-transition models）。上述模型均支持对成本和效用的模拟分析，适用于多种健康状态和时间点的数据。

PSM 作为决策支持工具，在本研究中展现了其优势与局限性。通过GetDataW 软件提取KN189 试验的PFS 和OS 数据，为生存分析提供了基础，避免了获取临床试验IPD 的需求。然而，PSM 的应用依赖于临床试验文献对生存曲线的详细报告，若需分析特定亚组或多状态患者的时间相关数据，而文献未提供必要信息时，分析可能受限。此外，PSM 能准确模拟疾病事件，但在随访时间超出临床试验报告时，需通过参数法外推PFS 和OS 曲线，这一过程对于晚期和转移性肿瘤药物的成本效用分析至关重要，但需要注意PSM 方法本身限制了敏感性分析的范围，当长期的总生存期外推存在不确定性时，局限性就会显现。因此，建议将PSM 与STM 一起使用，以支持对其推断的评估[4]。研究者需仔细检查外推拟合结果，利用个体临床事件的试验数据、外部数据和专家意见综合评估PSM 和STM 的生存预测可信度，避免出现不合理的统计现象[13]，后续进一步通过实例进行研究和说明。采用R 语言进行肿瘤治疗药物的成本效用分析要求研究者具备临床知识、数理统计能力及编程经验，研究者需在临床方案设计理解、参数设定、模型假设及验证等方面谨慎设定与检查，以确保分析结果的真实性和可靠性。

本研究聚焦于使用hesim 建立模型及PSM 辅助决策的视图功能，未能详尽阐述R 软件及相关程序包安装、PFS 和OS 曲线的数字化提取、参数分布的拟合与评估、生存分析的完整性及费用模型的数据来源和计算方法等内容，感兴趣的读者可参考文献[10-17]，以获取更多关于上述内容的详细信息。本研究为了突出PSM 模型建立，采用简单数值演示费用及效用模型，若需进行复杂的费用及效用模型分析，如疾病进展后多线治疗方案的比例、不良反应发生率及治疗费用等，则需单独建立模型，然后并入第5 步的实例化PSM，并进行概率敏感性分析。