大思政背景下《线性代数》课程混合式教学模式的改革研究

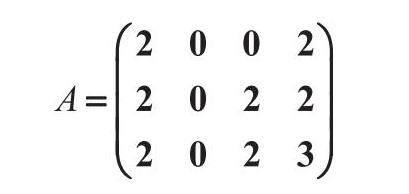
[摘要]为了提升教学效果和学生的自主学习能力，并结合张家界学院学生的实际情况，对《线性代数》课程开展了线上+线下的混合式教学，同时探索了该课程中蕴含的一些思政元素，以期达到润物无声的效果。

[关键词]混合式教学；课程思政；线性代数

[中图分类号]G641      [文献标识码]A

[DOI]：10.20122/j.cnki.2097-0536.2024.04.046

《线性代数》课程是针对于各高校理工类和经管类的本科一年级所开设的一门公共基础课程，也是考研数学中必考的科目之一，占比20%左右，主要内容包括：行列式、矩阵、线性方程组、特征值与特征向量、二次型[1]。该课程具有逻辑性强、抽象度高和应用性强的特点，实际应用覆盖各个领域，如航空航天、计算机通信、生物医疗、电力交通等都有广泛的应用[2]。学好该课程可以提高学生的抽象思维能力、逻辑推理能力以及应用代数知识解决实际问题的能力，同时也可以为学生学习后续的课程，如理论力学、材料力学、电路、数字信号处理等课程打下坚实的基础。

然而我们现在所教授的学生（本校的学生），通过问卷调查显示，80%的学生高考数学成绩在80分以下，95%的学生认为该课程的学习难度比较大；同时，学生思维非常活跃，对现代化的信息技术手段接受能力强。基于以上的学情和课程的特点，本文对传统的授课模式（PPT+板书）进行改革和实践，转变为线上+线下的多元混合式教学模式，并探索融入课程思政来提升教学的温度和效果。

一、线上+线下混合式教学模式的设计与实施

结合传统课堂教学和网络在线教学的优势，依托超星泛雅平台，我们建立了在线开放课程，在平台上借助于示范教学包，已导入18个授课视频（视频总时长985分钟）、非视频资源82个、发帖总数18094。丰富的在线资源保障了线上+线下混合式教学模式的开展，依托现代信息技术手段，我们构建了“三阶段”的授课模式，即课前、课中、课后：课前，教师在学习通上提前发布教学任务，学生提前在平台上观看相应的教学视频、完成自测，并将学习中的难点问题提前标注，教师通过后台数据实时督促学生们完成预习任务，并以线上讨论的方式汇总学生在自学过程中出现的难点问题；课中，针对学生们在课前出现的难点问题，教师以在线下课堂上通过案例教学法、问题驱动法等方式进行重点的讨论和讲授，并且利用学习通的随堂练习、抢答、选人、投票等方式进行课堂互动，一方面可以提高学生的课堂参与度，另一方面教师可以掌握到每个学生课堂学习的效果；课后，教师通过发布任务点检测、线上作业、线上讨论、和章节测试等方式用于学生们进行课后的自我提升，也会通过学习通平台、微信、QQ等方式对学生出现的问题进行答疑解惑。这种“三阶段”的授课模式极大程度拓展了课程教学的时间和空间，也让学生在课后真正的忙起来和动起来。

二、课程思政元素的探索和实施

《线性代数》课程作为公共基础课受众面广，因此这门课为思政教育提供了很好的平台。为了让课程思政自然地贯穿于教学的全过程，我们深度挖掘和探索了该门课程所蕴含的思政元素，主要从哲学思想、数学思想、文化自信、爱国情怀、科学精神、正确的三观等思政元素入手，得到了以下的思政案例。

（一）融入哲学思想

数学家德莫林斯（B.Demollins）说：“没有数学，我们无法看穿哲学的深度，没有哲学，我们也无法看穿数学的深度，而若没有这两者，我们什么也看不清”，这充分说明数学与哲学密不可分，线性代数课程蕴含着丰富的哲学思想。

案例1：对比行列式与矩阵的区别及讲解和时（这里的向量都是列向量，前者算出来是一个矩阵，后者本质上就是一个数），引出“现象与本质”的辩证关系，教会学生要学会透过现象看到本质。

案例2：矩阵的初等变换和初等矩阵、利用初等变换化矩阵为行阶梯形和行最简形所蕴含的“变与不变”的辩证思想。

案例3：向量组的线性相关与不相关、矩阵的可逆和不可逆、二次型的正定与负定所体现的“对立与统一”的辩证思想。

案例4：利用方程组的系数矩阵和增广矩阵的秩来判断方程组是否有解问题中所蕴含的“量变与质变”的辩证关系。

（二）融入数学思想

案例5：利用“倒数”概念理解“逆矩阵”，利用数字“1”来理解单位矩阵，通过这样的类比思想提升学生的数学素养和创新思维。

案例6：在讲解行列式按行按列展開时，将高阶行列式化成低阶行列式；在讲解二次型的正定性，利用矩阵来化成标准形；通过划归思想将数学中复杂的问题转化为简单问题，从而化繁为简、化难为易。

案例7：利用逆矩阵进行信息的加密和解密处理时，通过数学建模的思想让学生感受到线性代数的实际应用，从而激发学生学习的兴趣。

（三）融入文化自信、爱校爱国情怀以及中国传统文化

案例8：在讲解线性方程组时，引入中国著名数学著作《九章算术》，该著作中研究解线性方程组时使用的直除法与矩阵的初等变换一致，这也是世界上最早的完整的线性方程组的解法，比欧洲至少早了1500年（直到17世纪才由莱布尼兹提出完整的线性方程的解法法则），让学生感受到中国古代数学的辉煌成就，激发学生爱国情怀。

案例9：在讲授矩阵的定义时，巧妙地构造矩阵。

告诉学生吉首大学张家界学院成立于2002年，2022年是学校建校20周年，2023年是学院发展的关键之年，学院将成功转设为独立设置的普通本科高校。通过讲解学校的发展历史，增强学生的归属感和荣誉感，激发学生对学校的自豪感、使命感和责任感。

案例10：在每一章学完后，我们都会引入由东南大学张小向教授为《线性代数》课程填写的七言律诗，例如为行列式写的七律“众数纵横成方阵，多少玄机藏其中。行列算尽得一值，却是智取胜强攻。奇次对换变符号，转置倍加果相同。妙手巧化繁为简，八仙过海显神通”。该首诗词的第一句、第三句道出了行列式必须是一个方阵，本质就是一个数；第五、六句道出了行列式的性质，让学生在欣赏诗的同时，也深入理解了线性代数有关概念，更领略了中华传统诗词之美。

（四）融入科学精神

案例11：学习数学家的先进事迹，如法国数学家范德蒙德—行列式理论的奠基人、瑞士数学家克拉默—克拉默法则、英国数学家西尔维斯特—矩阵概念的提出者、清代数学家李善兰—首次把“Algebra”翻译成代数，培养学生勇攀科学高峰的科学精神。

案例12：通过引入线性方程组在中国自主研发的北斗卫星导航系统BDS（2020年7月31日，北斗三号全球卫星导航系统正式开通，全球一共四大导航系统）中的应用，用“北斗精神”引导学生关注国家大事、感受“大国制造”的魅力，同时体会中国科技知识强国梦。

（五）融入做人做事的基本道理及正确的价值观

案例13：利用矩阵乘法不满足交换律，但是满足结合律来计算，从而引导学生做人、做事要遵守规则、遵守法律，同时也要学会利用规则、提升能力。

案例14：在介绍拉普拉斯定理时，让学生做游戏，意选8个数构成一个八阵图：

然后将这些数字按照在矩阵中的排列顺序分为两组，相乘再进行加减运算，即为：

利用拉普拉斯定理，學生很容易发现上面的八阵图游戏计算形式与定理的计算形式类似，事实上：这个行列式始终等于0（行列式有两行完全一样），从而破解“八阵图游戏玄机”。

该八阵图游戏是日本一个小寺院大和尚所展示的“玄机”，由于日本人崇尚数字0，因为0和“灵”相通。游客来这里问卜，得到的总是他们喜欢的“0”，也正因为这个原因，寺庙才游客不断。通过游戏的方式让学生感受到数学的魅力和价值，从而使学生“相信科学，反对迷信”。

三、结语

在信息化时代，这种线上+线下的多元混合式教学模式确保了师生交流的超时空性，增加了课堂教学的容量，提高了教学的有效性；既能发挥教师的主导地位，也能充分发挥学生的主体地位，同时还可以提高学生的自主学习能力。自然地融入思政能使教学变得有温度，把课堂变成一个有情有义有爱的教学过程，但课程思政任重道远，在今后的教学中还要不断地探索和挖掘课程中蕴含的思政元素，以期达到润物无声的教学效果[3]，落实立德树人的根本任务。

参考文献：

[1]赵立军.线性代数[M].北京：北京大学出版社，2019.

[2]胡军，杜军花，徐龙，等.“互联网+”背景下线性代数混合式教学方法探讨[J].高师理科学刊，2021，41（3）：79-83.

[3]刘红霞.“线上线下 混合式学习”模式下线性代数课程思政建设的新探索[J].济南职业学院学报，2021（1）：45-47.

[4]王涛，马新顺，郭燕.《线性代数》课程思政的案例及思考[J].数学学习与研究，2020（10）：54-55.

[5]阎昕明，田德路，张然然.《线性代数》课程混合式教学的设计与实施[J].广东第二师范学院学报，2020，40（5）：106-112.

基金项目：张家界学院院级教学改革研究项目资助，项目名称：大思政背景下《线性代数》课程混合式教学模式的改革研究（项目编号：Jxjg2112）

作者简介：秦晶（1988.6-），女，土家族，湖南永顺人，硕士，讲师，研究方向：应用数学。