基于改进混沌算法的供热机组热电负荷优化分配系统

韦淑敏

（国网湖南供电服务中心（计量中心），湖南长沙 410007）

混沌算法是一种为混沌序列加密算法，通过单向Hash 函数求解密码序列表达式，并根据混沌映射条件，计算迭代初值指标的取值范围[1]。考虑到混沌映射条件对于数据样本的承载能力有限，在构建混沌算法时，要求同一Hash 函数区间内数据样本的最大取值不得超过密码序列对于信息参量的最大承载能力[2]。改进混沌算法是传统混沌算法的优化形式，能够通过混沌序列提升加密能力，既可以增大Hash函数区间对于数据样本的承载能力，并定义全新的混沌映射条件，从而使得迭代初值指标的取值范围可以更好匹配加密算法表达形式。

对于供热机组设备而言，如何在保证热电负荷拟合效果的同时，控制供热机组的实际耗能量水平成为了一项亟待解决的问题。基于Ziegler-Nichols优化算法的PID 控制技术根据电网负荷峰谷差数值，对供热机组的热电负荷水平进行调节，再通过求解PID 控制指标的方式，确定机组设备的实际耗能量[3]。基于大数据技术的优化分配方法以模糊粗糙集理论为基础，在分配热电负荷的同时，完成对热电负荷曲线的拟合处理[4]。然而上述两种方法不能有效控制热电负荷参量与标准拟合曲线之间的误差水平，故而并不能实现对供热机组耗能量的按需分配与节约。为解决上述问题，针对基于改进混沌算法的供热机组热电负荷优化分配系统展开研究。

1 分配系统设计方案

供热机组热电负荷优化分配系统借助主供热单元，对热电负荷循环模式进行完善，从而实现对负荷参量的按需布置，具体设计方法如下。

1.1 主供热单元

供热机组热电负荷优化分配系统的主供热单元由继电元件、供热设备、负荷电阻三部分共同组成。其中，继电元件接收外部输入的电负荷参与与热负荷参量，并可以利用多个已连接的负荷电阻R，对负荷参量进行平均分配处理，从而避免热量信号、电量信号出现不匹配问题，使得热电负荷循环回路内的传输信号始终保持相对稳定的状态[5-8]。完整的主供热单元回路连接结构如图1 所示。

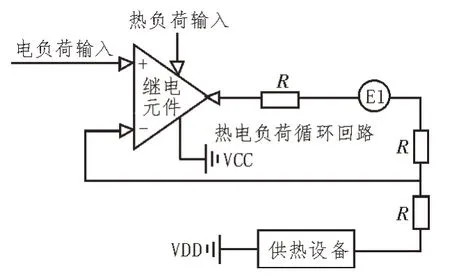
图1 主供热单元回路

热负荷、电负荷均以正极节点作为接入位置，在节点元件接入主供热单元回路的情况下，负荷参量完成输入后，首先，通过热电负荷循环回路，然后，在供热设备中大量聚集，最后，经由传输回路，回传至继电元件负极节点。

1.2 热电负荷循环模式

热电负荷循环模式就是指负荷参量在供热机组内的循环形式（如图2 所示），由于主供热单元对于电量信号的负载能力有限，所以机组设备内热信号传输量始终大于电信号[9]。

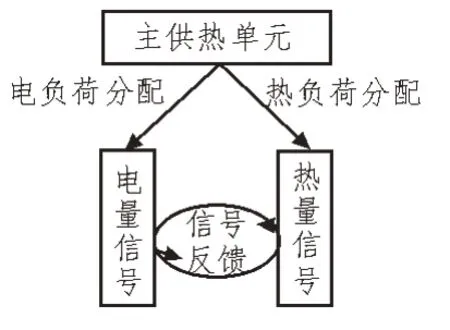
图2 热电负荷循环模式

设s表示热电负荷转化系数，φ表示电信号输出量，φ表示热信号输出量，d˙表示负荷信号循环特征。在上述物理量的支持下，构建推导热电负荷循环模式表达式为：

由于φ系数取值恒大于φ系数，所以热电负荷循环模式表达式计算结果不大于自然数“1”。

1.3 热电负荷优化布置

热电负荷优化布置就是依照改进混沌算法元件，对热电负荷信号进行分配处理。一般来说，待分配的电负荷信号总量越大，完成优化布置后的信号覆盖面积也就越大[10-12]。规定λ′表示主供热单元内的热电负荷量残差值，λ0表示热电负荷量残差的初始取值，联立式（1），可将基于改进混沌算法的热电负荷优化布置表达式定义为：

2 供热机组热电负荷分配的数学模型

2.1 约束条件

单纯的混沌算法可能会忽略罚向量（热电负荷参数）的取值区间，从而使得优化分配系统失去准确判断供热机组热电负荷水平的能力，通过设计供热机组热电负荷分配的约束条件，获取改进罚函数条件，定义罚向量（热电负荷参数）的取值约束条件。由于约束条件只影响罚向量取值范围，故而只有当罚向量取值属于热电负荷参数赋值范围之内时，按照改进罚函数推导所得的约束条件才成立。

改进混沌算法约束条件定义式为：

其中，γ表示罚向量赋值参数，ℜ 表示热电负荷参数赋值区间。由于约束条件直接影响改进混沌算法的作用能力，故而其赋值方向与改进罚函数直接相关。

2.2 混沌算法的改进

混沌指数决定了混沌算法的基本特性，在对供热机组热电负荷进行分配处理时，混沌算法影响机组设备对于热电信号的提取能力，因此混沌指数取值是否合理是构建优化分配系统的关键步骤[13]。

规定i表示混沌偏差项，pi-1表示与第i-1 个偏差项相关的负荷参数，β表示分配系数，联立上述物理量，计算第i个负荷参数pi，如下：

求解pi相反数，如下：

混沌指数表达式为：

其中，α表示迭代参数，ui表示第i个偏差项的混沌化程度。混沌化程度不具有关联性，所选取混沌化参数只影响当前偏差项的混沌水平。

一般性罚函数可表示为：

其中，u为罚向量（热电负荷参数），χ(u)为理想约束函数，δ(u)为理想导向量函数，ε(u)为可导函数。

利用混沌指数改进罚函数[14]，推导计算式为：

其中，χ′(u)为约束函数改进条件，δ′(u)为导向量函数改进条件，ε′(u)为可导函数改进条件。混沌算法要求罚函数具有可导能力，故而函数表达式改进方向不得违背罚向量（热电负荷参数）可导条件[15]。就此完成供热机组热电负荷优化分配系统设计。

3 实例分析

3.1 拟合误差分析

热电负荷参量与标准拟合曲线之间的误差水平可以反映出热电负荷信号的拟合效果，直接影响供热机组的实际耗能量[16]。

对于拟合误差的求解满足式（9）：

其中，σmax表示热电负荷参量的最大取值，σ0表示当前时刻标准拟合曲线热电负荷参量的取值。

图3 为该次实验所选的LSQWRF100 供热机组设备。

图3 供热机组

对于LSQWRF100 供热机组而言，热量探头采集到的电负荷信号、变电板输出的电负荷信号可以在换热装置的作用下，进行直接转换，所以热量负荷与电量负荷的损失情况都能得到较好控制，故而热电负荷参量与标准拟合曲线之间的误差值越小，表示供热机组的实际耗能量越小。

3.2 拟合误差实验

选择基于改进混沌算法的优化分配系统、基于Ziegler-Nichols 优化算法的PID 控制技术、基于大数据技术的优化分配方法作为待测实验方法，第一组方法为实验组，后两组方法分别为对照组A和对照组B。

图4 反映了实验组、对照组热电负荷参量与标准曲线之间的拟合情况。

图4 拟合曲线

分析图4 可知，实验组方法作用下，热电负荷参量曲线的曲率变化程度较小，整个实验过程中，其负荷量数值与标准拟合曲线之间的差值水平也相对较低；对照组A 方法作用下，热电负荷参量数值一直保持不断增大的变化态势，实验结束时，其负荷量数值与标准拟合曲线之间的差值水平最高；对照组B 方法作用下，热电负荷参量数值保持先上升、再下降的变化情况，实验时间等于4 h 时，其负荷量数值与标准拟合曲线之间的差值最大。

取热电负荷参量与标准拟合曲线之间的最大差值，对拟合误差进行计算，详情如表1 所示。

表1 拟合误差

分析表1 可知，应用实验组方法所得的拟合误差值最小，应用对照组A 方法所得的拟合误差值最大，与实验组差值为40.0%；应用对照组B 所得的拟合误差值处在实验组方法、对照组A 方法之间，与实验组差值为38.7%。所设计系统可以将热电负荷参量与标准曲线之间的拟合误差控制在30%以内，与两种传统方法相比，在控制供热机组实际耗能量方面具有突出应用能力。

4 结束语

供热机组热电负荷优化分配系统在改进混沌算法的基础上，求解了约束条件的应用表达式，又根据主供热单元对于热电负荷循环模式的影响能力，确定热电负荷的优化布置形式。随着这种新型分配系统的应用，因热电负荷拟合效果不佳导致的供热机组实际耗能量增加的问题得到了较好解决，在实用性方面，该系统确实与设计初衷更加贴合。