基于改进的禁忌搜索算法在有序用电中的应用
2024-05-06王卓城杜江帆段凤熙黄惠倩蔡伟鸿
王 烁,王卓城,杜江帆,段凤熙,黄惠倩,蔡伟鸿
(1.广东电网有限责任公司汕头供电局,广东 汕头 515041;2.汕头大学数学与计算机学院计算机系,广东 汕头 515063)
0 引 言
随着电力等清洁能源受到越来越多关注,电力系统负荷与日俱增,用户用电数据海量增长,政府及用户对电力企业的电力信息调度系统的智能化建设提出了更高的要求.为了促进电力供需平衡,保障电网稳定运行,国内外学者主要围绕需求响应和有序用电提出解决方案.需求响应手段包括市场化调整、补贴激励、分时电价等.当灵活需求响应仍不能满足电网的稳定运行时,就需要有序用电手段的参与,维护供用电秩序平稳有序的管理工作.有序用电的主要措施有削峰填谷、错峰避峰、拉闸限电等.如何在衡量高效性和公平性的基础之上选出参与有序用电的用户组合以填补负荷缺口,是一个值得研究的重要问题.
许多实际的工程和管理问题可以被提炼为优化问题,通过优化方法快速找到最优解决方案,以实现最佳效益,并最大限度地提高生产效率[1].在最近几年中,随机搜索优化算法备受关注,因为它可以高效地解决现实世界中的复杂优化问题,具有求解准确度高、速度快、成本低和强鲁棒性等优点.相比于传统的优化算法,随机搜索算法较少关注目标问题的梯度信息,并且易于进行计算机编程实现[2].在诸多随机搜索算法中,群体智能优化算法(Swarm Intelligence Optimization Algorithm,SIOA)备受科学研究者的关注和改进. SIOA 是参考个体之间为了求得生存和发展而展现出独有的协同自适应行为,如觅食、迁徙、求偶等,来对复杂问题进行求解.例如,受蚂蚁搜索行为启发的蚁群优化算法对结构优化问题[3]、交通区域控制问题[4]以及基因组优化问题[5]等都具有良好的应用效果;粒子群优化算法对双边规划问题[6]、电力系统[7]、海洋石油存储[8]和图像处理等[9]问题的解决带来了便利.其中,在电力领域,大量研究成果表明个体间相互作用所构成的群体行为对解决智能电网系统的复杂优化问题十分有效.因此,SIOA 的不断发展和广泛应用为电力系统优化问题提供了新思路.
禁忌搜索算法(Tabu Search,TS)是一种启发式邻域搜索算法.该算法从迭代中的可行解开始,依照预定义的移动策略生成一组相邻解,最后使用其最佳邻域解替换可行的解决方案[10].同时,禁忌搜索中的邻域解提供了同时评估多个目标函数的机会,因此它可被用于解决多目标优化问题.Moch 等将禁忌搜索过程和遗传算法相结合,以解决最大限度减少流水车间调度的单目标优化问题,平衡探索和开发能力[11].Maria da 和Luisa等提出一个搜索算法来设计最低成本的循环配水网络,在经典配水网络案例上产生一个更高质量的解决方案[12].Martínez-Puras 和Pacheco 提出了一种周期性车辆路由问题的解决方案,该方法结合了禁忌搜索和多目标自适应记忆编程策略,并与非主导排序遗传算法相比,表现出更好的性能[13].
如文献所述,禁忌搜索具有很强的本地搜索能力,在解决大规模的复杂优化问题上非常有竞争力[14].然而,尽管它在单目标优化问题中很受欢迎,但使用多目标版本的禁忌搜索来处理有序用电中的用户组合调配负荷缺口问题的成果较少.因此,为了加强禁忌搜索在多目标问题上的应用,同时,为了满足智能电网安全、可靠、高效的需求,本文提出了一种基于改进的禁忌搜索算法,用于搜索多目标电网用户组合的最优解.
1 有序用电用户调度能力的组合优化问题
1.1 问题建模
在有序用电项目中,主要有两种角色,一是电能供应商,二是使用电力的用户,一般在存在负荷调控潜力的用户群体中挑选.在电力需求响应政策无法维持电网稳定运行时,为了协调好供应方和需求方之间的关系,将启动有序用电方案.供电方先对用户电力调度能力进行预测,即用户即将可能上调或减少的用电量.供电方根据电力主管部门下达的网供指标选择需要调整用电量的用户,在满足网供指标的情况下,选择最优用户组合来最小化总用电量.确定用户组合后,供应方会告知用户电力目标,用户根据自身情况自愿参与需求响应.
1.2 约束条件
为了便于供电方有效安排有序用电,选出同时满足指定条件的用户组合,需要满足以下条件:
(1)所选择用户电力调度能力的组合必须超过且尽可能接近网供指标,网供占比设置为100%-105%
用户电力调度能力由电力企业提供,描述用户可能增加或减少的用电负荷,用以填充负荷缺口.日网供指标是由电力主管部门下达,在保证电力系统可以稳定运行之下规划的指标,代表着电力系统当日可以提供的总电量.为了防止用电量使用不足导致的浪费,安排的用户组合必须超过指标.同时,由于用户不一定会根据电力企业的要求严格执行,本文上调网供占比至105%以保证模型的可扩展性.网供占比为用户实际用电量占网供指标的百分比,描述了用户的具体实施情况,用来衡量算法在有序用电问题上的有效性.
(2)在有序用电任务较紧迫的情况下,优先考虑调度的高效性
优先考虑高效性时,算法要求尽可能让较少的用户被选择,即尽量选择用电预测可调度负荷较大的用户,以减少供电企业员工的工作量,高效调配用电用户来填充负荷缺口.
(3)在有序用电任务能允许更灵活的时间计划时,优先考虑调度的公平性
优先考虑公平性时,算法要求下次调度不再选择最近被选择过的用户.尽量避免部分可被分配且有被调度期望的用户长时间不被选择,同时避免部分可调度负荷较大的用户反复被选择,保证用户友好性.
1.3 问题描述
根据1.1 节和1.2 节对项目模型和约束条件(1)的描述,本文需要在尽量满足供电方和需求方双方需求的条件下,选择出最优的用户组合,具体的目标函数如式(1)所示.
其中,N 表示用户总数;ei表示用户i 的电力调度能力;xi表示用户i 是否被选中,1 代表被选中,0 代表未被选中;T 表示网供指标.第一个约束条件表示所选中用户组合的电力调度能力之和不得少于网供指标.
根据1.2 节对约束条件(2)和约束条件(3)的描述,本文模型还需要同时满足电力分配的高效性和公平性,因此设置一个适应度函数以评判所选用户对于约束条件的匹配程度,具体的适应度函数的数学表达式如式(2)所示.
其中,ti表示用户i 的等待时间,即距离上一次被调配的间隔天数;e'i表示归一化后的用户i 的电力调度能力,归一化调整电力调度能力至与等待时间同一数量级;w1、w2是常数,分别代表了用户等待时间和用户电力调度能力的权重. 需要优先考虑公平性时,w1>w2;需要优先考虑高效性时,w1<w2,具体数值根据实际情况设定.
2 改进的禁忌搜索算法
2.1 禁忌搜索算法(TS)
禁忌搜索是一种基于局部搜索的元启发式算法,由弗雷德·W·格洛弗(Fred W.Glover)在1986 年首次提出[15].该方法不要求获得最优精确解,而是获得次优解的近似方法.TS 算法属于迭代寻优算法,算法从初始可行解开始,通过最大下降来找到更好的解.与传统的最大下降搜索方法不同,TS 算法采用灵活的短期记忆系统来防止重复搜索[16].禁忌列表中保存的解决方案在下次筛选最优解候选时将不再录用,这些解决方案被称为禁忌.而且TS 算法允许回溯到之前的解,这种能力允许所得解向客观价值恶化的方向移动搜索. 因此,它有望从局部最小值中逃逸出来,走向全局最优解,最终获得更优的解[17]. TS 算法主要由禁忌列表(Tabu List,TL)约束和与约束相关的特赦水平(Aspiration Level,AV)两部分组成,禁忌列表是用来限制搜索过程中重复探索已经搜索过的解,特赦水平是用来避免陷入局部最优解的限制条件.通过灵活地设置禁忌列表和特赦水平,可以有效地平衡全局搜索和局部搜索,不断地搜索邻域解来逐步改进当前解,从而找到满意的解.
TS 算法先随机生成一个可行解,并利用邻域搜索方法在当前解的邻域内探索相邻解,直到找到满足特定条件的解为止. 在搜索相邻解的过程中,如果该解不在禁忌列表(TL)中,或者虽然在TL 中但符合特赦水平,就接受该解并对其进行评估. 在生成的相邻解中,选择目标函数值最佳的邻域解作为下一个解,直到达到预定的停止条件.禁忌搜索算法的算法流程如图1 所示.禁忌搜索算法的伪代码如下所示:
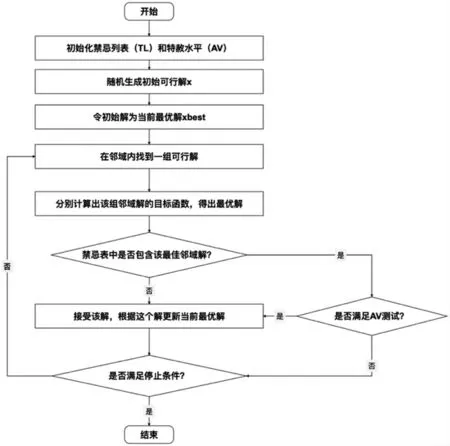
图1 禁忌搜索算法流程图
禁忌搜索具有避免陷入局部最优解的优点,通过由禁忌表构成的短期记忆系统防止重复搜索.对于低维度问题,禁忌搜索算法可以得到不错的结果.然而,对于大型问题,禁忌搜索算法可能会受到限制,因为其需要占用大量的资源来处理解空间.与此同时,对于一个SIOA 来说,初始化的好坏在一定程度上决定了算法的优化性能.禁忌搜索算法的初始化是以随机的方式产生的,当目标值相对数据较小,且简单随机所选出的初始解距离最优解距离非常远时,在可行解的邻域内很难搜索到最优解.有一种新颖的启发式算法:野狗优化算法,在大量基准测试函数中与其他经典的启发式算法相比具有明显的竞争力,可以最有效地达到全局最优且平均绝对误差最小,在迭代的初始阶段就能迅速收敛[18].野狗优化算法的迭代机制非常适合用来改进禁忌搜索算法上的缺陷.因此,本文选用野狗优化算法来改进禁忌搜索算法的初始化阶段,以选出更优的初始可行解来提高算法性能.
2.2 野狗优化算法(DOA)
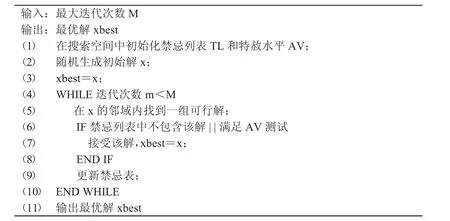
野狗优化算法(Dingo Optimization Algorithm,DOA)是一种由澳洲野狗的狩猎策略启发的群体智能优化算法,该算法根据野狗的社交行为,设计了三种策略,分别为群体围剿、单独攻击、清扫行为.同时,该算法中加入了生存概率策略[18].以上多策略形式给DOA 算法带来快收敛的优势.DOA 算法的流程如图2 所示.
图2 野狗优化算法(DOA)流程图
2.3 利用莱维飞行改进的野狗优化算法(LDOA)
由于启发式算法只求找到一个次优解,通常采用贪心策略或局部搜索策略,并对问题进行一定程度的简化,从而使问题变得更易处理,这导致容易陷入局部最优成为了大部分启发式算法难以避免的通病.尤其是收敛速度较快的算法,可能会过早地收敛到局部最优解.因此,即使DOA 在效率上比其他启发式算法有明显的优势,仍存在达不到全局最优的可能.
避免陷入局部最优的最好方法就是随机,具体原则主要有三类:越随机越好、越不随机越好、二者平衡.通常情况下,第一类可以提高搜索的鲁棒性,稍微改善算法性能,但过多的随机性可能导致搜索过程变得盲目和低效;第二类是在搜索过程中加入更多的启发式信息或者约束,使搜索过程更有针对性;将二者适当调和则会带来综合性的飞跃.与混沌理论有关的莱维飞行算法正是一种结合了随机性和非随机性的改进[19],广泛应用于对随机和伪随机自然现象的模拟.该算法在随机步长上进行变异,采用了短距离搜索和长距离行走相间的方式,在随机行走的过程中存在相对较大的几率出现大跨步,有助于算法局部最优解的逃逸[19].因此,本文使用莱维飞行对DOA 算法每轮迭代得到的次优解进行扰动操作,防止其陷入局部最优.
莱维飞行的轨迹由式(3)模拟.
其中,xi(t)代表第t 代的第i 个解;l 是控制步长的权重;⊕是点乘;表示服从莱维分布的路径.由于莱维稳定分布非常复杂,目前主要使用Mantegna 算法来模拟[20],由式(4)计算步长.
其中,μ 和v 服从正态分布;γ 是一个常数因子,通常取值为1.5.
分别对莱维飞行策略和普通随机策略进行仿真,仿真步长为1 000,结果如图3 所示.由于特殊的步长变异方式,莱维飞行同时存在足够的随机变化和更大的搜索范围,小步长有利于随机在当前最优解附近搜索,而大步长有利于跳出局部最优、进行全局搜索.
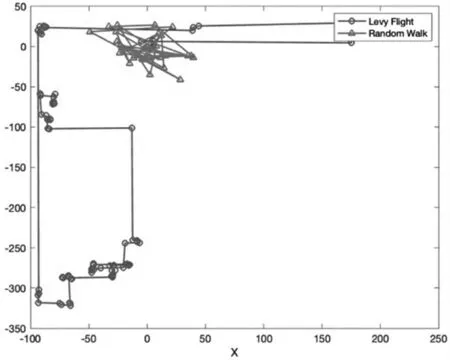
图3 莱维飞行策略和普通随机策略仿真
DOA 算法跟其他算法相比在收敛速度上有明显优势,因此陷入局部最优的概率也更大.使用莱维飞行对DOA 算法改进得到LDOA 算法,LDOA 算法的流程图如图4 所示,在未达到最大迭代次数且适应度值变化趋于平缓时,在下一轮迭代前根据式(3)使用莱维飞行策略优化当前解,可以达到防止算法陷入局部最优的目的.

图4 使用莱维飞行策略改进的野狗优化算法(LDOA)算法流程图
2.4 基于改进的禁忌搜索算法(LDOA-TS)
为了尽可能避免随机初始解导致的禁忌搜索收敛速度较慢,本文提出使用改进的野狗优化算法对禁忌搜索进行种群初始化,提出一种改进的禁忌搜索算法(LDOA-TS),该算法的算法流程图如图5 所示.

图5 改进的禁忌搜索算法流程图
LDOA-TS 算法的伪代码如下所示:

使用莱维飞行改进野狗优化算法得到莱维野狗优化算法(LDOA),使其容易跳出局部最优.然后使用LDOA 算法来优化禁忌搜索的初始化部分得到LDOA-TS 算法,降低禁忌搜索算法由初始化不佳导致的最优解不稳定的问题,同时加快了禁忌搜索的收敛速度.给禁忌搜索带来较大的提升.
3 实验对比分析
3.1 实验参数设置
为了考察本文提出的LDOA-TS 算法的性能,本文将设计消融实验和对比实验.结合本文模型的要求以及现有的启发式算法在解决优化问题时的参数设置,设置具体参数如表1 所示.

表1 实验参数设置
3.2 实验数据处理
本文以广东省汕头市为例,使用南方电网提供的实际生产数据,对上述算法进行实例分析验证.为了更好地验证本文设计的混合禁忌野狗优化算法在不同数量级的数据上具有的实用价值,实验将数据集筛选为某小区(50 户)、某街区(500 户)、某行政区(5 000 户)分别进行实验.为了方便数据处理,将用户电力调度能力数据映射到[0,1]范围内.由公式(5)(6)实现,power 代表用户用电调度能力,normalized_power 代表归一化后的用户用电调度能力,wait_days 代表用户未被调度的天数,normalized_wait代表归一化后的未被调度天数.
3.3 实验结果对比与分析
为了验证算法的各个优化部分对于算法的提升效果,本文对算法设置对照组,设计TS 算法、DOA 算法、LDOA 算法、DOA-TS 算法作为LDOA-TS 算法的消融实验.为了验证本文算法(LDOA-TS)的有效性,将本文的LDOA-TS 算法与经典的人工鱼群算法(AFSA)[21]、使用莱维飞行改进的遗传算法(LGA)[22]、蜜蜂算法(BA)[23]、蚁群算法(ACO)[24]、细菌觅食优化算法(BFOA)[25]进行对比.同时,为了避免随机性对寻优结果的影响,实验以不同的用户数量和对应指标各个算法均独立运行100 个周期,并分别记录平均指标占比、平均方差、平均适应度值.其中,指标占比是指算法选出的用户电力调度能力和占网供指标的百分比,可以反映出结果数据的达标程度,平均方差用来反映算法的稳定性,平均适应度值越大证明越符合用户数量少、等待时间短的要求.
图6 是禁忌搜索算法(TS)和改进的禁忌搜索算法(LDOA-TS)在相同条件下,分别运行100 个周期的平均指标占比(Percentage)的结果图.图6(a)是N=50、Target=100的结果,图6(b)是N=500、Target=1 000 的结果,图6(c)是N=5 000、Target=10 000的结果.将数据进行对比,可以看出LDOA-TS 算法的鲁棒性比TS 算法更好,且用户数量规模越大,优势越明显.

图6 TS 算法和LDOA-TS 算法在不同条件下的平均指标占比
表2 展示了当N=50,Target=100、N=500,Target=1 000、N=5 000,Target=10 000 时,各个算法运行100 个周期的平均指标占比(Percentage)、平均标准差(σ)、平均适应度值(Fitness).在用户数量较少时,各个消融算法在平均指标占比上基本满足条件,LDOA-TS 算法、DOA-TS 算法、TS 算法满足程度最高,平均适应度值也最高,更好地平衡供需双方的需求.而LDOA-TS 算法、DOA-TS 算法的平均标准差明显小于其他算法,证明稳定性更高.此时,与DOA 算法相比,LDOA 算法的平均标准差优势不明显.随着用户量上涨,LDOA-TS 算法的稳定性展现出明显的优势.当用户数较大时,与DOA 算法相比,LDOA 算法的平均标准差明显较小.由此可以证明莱维飞行对野狗优化算法改进的实效性,而融合了莱维飞行的野狗优化算法对禁忌搜索算法的优化也很明显.
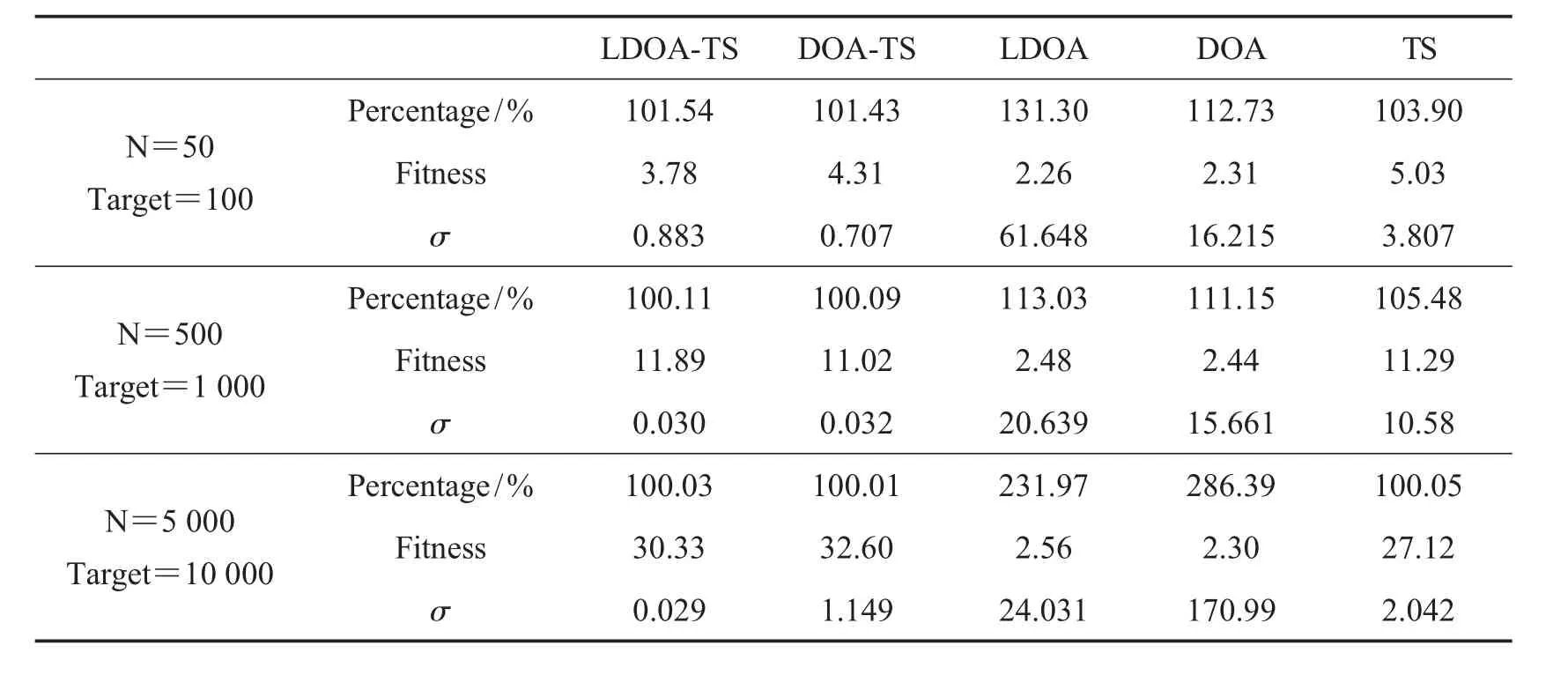
表2 不同用户数量级求解问题的消融实验结果
图7 展示了N=50,T=100 时,各个算法的平均指标占比和适应度值在迭代过程中的变化.由图7 显示的实验结果可以看出,在用户量较小的条件下,各个算法都能满足指标占比不小于100%并且不大于105%的要求,且尽可能接近100%的供电方需求.与TS 算法相比,DOA 算法的初始化解明显更接近于最优解,LDOA 算法和LDOA-TS算法更甚,且明显在较少的迭代次数内收敛到最优值.LDOA 算法和LDOA-TS 算法的适应度值最高,接近DOA 算法和LDOA 算法的两倍.

图7 用户量为50 的平均指标占比和适应度值变化
图8 展示了N=500,T=1 000 时,各算法的平均指标占比和适应度值在迭代过程中的变化.当用户量上涨时,DOA 算法、LDOA 算法、DOA-TS 算法、LDOA-TS 算法与TS 算法的对比优势愈加凸显.DOA-TS 算法和LDOA-TS 算法以极低的初始值,极少的迭代次数迅速收敛到了全局最优,得到可接受的解决方案.同时,LDOA-TS 算法适应度值是最大的,表明在同时满足参与用电量调度的用户数量较少以及避免部分用户等待时间过长的两个条件下,LDOA-TS 算法的效果得到了显著提升.
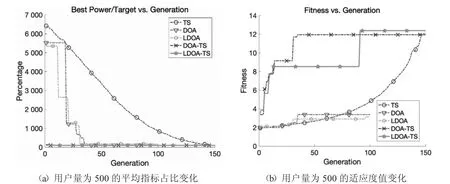
图8 用户量为50 的平均指标占比和适应度值变化
图9 展示了当N=5 000,T=10 000 时,各个算法的平均指标占比和适应度值.当用户数量和网供指标较大时,与TS 算法相比,DOA 算法和LDOA 算法以极快的迭代速度收敛,使得DOA-TS 算法和LDOA-TS 算法得到较优的初始值,收敛速度也因此提升.TS 算法、DOA-TS 算法和LDOA-TS 算法的适应度值较大,其中LDOA-TS 算法的适应度值略高于DOA-TS 算法.
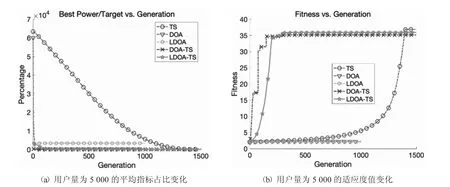
图9 用户量为50 的平均指标占比和适应度值变化
图10 展示了将LDOA-TS 算法与多个经典启发式算法在不同用户数量、和对应网供指标下进行的对比实验结果.对比的算法包括:人工鱼群算法(AFSA)、使用莱维飞行改进的遗传算法(LGA)、蜜蜂算法(BA)、蚁群算法(ACO)、细菌觅食优化算法(BFOA).

图10 对比实验结果
图10(a)为N=50,Target=100 时,各迭代30 次的网供指标占比;图10(c)为N=500,Target=1 000 时,各迭代50 次的网供指标占比;图10(e)为N=5 000,Target=10 000 时,各迭代50 次的网供指标占比.观察可得,本文的算法LDOA-TS 在与各个经典算法的对比实验中最快收敛到最优解,AFSA 算法和ACO 算法次之,BA 算法、LGA 算法和BFOA 算法在收敛速度的优势上不太明显.图10(b)为N=50,Target=100时,各迭代30 次的适应度值;图10(d)为N=500,Target=1 000 时,各迭代50 次的适应度值;图10(f)为N=5 000,Target=10 000 时,各迭代50 次的适应度值.观察可得,在用户量较小时,本文提出的LDOA-TS 算法和经典的AFSA 算法的适应度值最大,即在平衡有序用电的高效性和用户友好性上表现得较好.当用户量较大时,AFSA 算法对适应度值最大,本文提出的LDOA-TS 算法次之,BA 算法、LGA 算法、ACO 算法和BFOA 算法在适应度值上表现较为不佳.随着用户量增长,LDOA-TS 算法在平衡有序用电的高效性和用户友好性上仍能维持较优的水平.
由以上实验结果可以观察得出,LDOA-TS 算法、AFSA 算法、LGA 算法、BA 算法、ACO 算法、BFOA 算法都能基本满足用户用电调度能力组合尽可能接近网供指标的电力需求,其中LDOA-TS 在初始解的选择、收敛速度、电力需求达标的综合情况上表现得更好一些.在满足网供负荷条件下,LDOA-TS 算法和AFSA 算法的适应度值是最优的,更能平衡供需.
4 结 论
本文使用融入了莱维飞行的野狗优化算法对禁忌搜索算法的初始化过程进行优化,得到一种基于改进的禁忌搜索算法LDOA-TS,并将该算法应用于有序用电时搜索多目标电网用户组合的最优解的问题,同时选用控制变量下的4 个消融实验和其他性能较好的算法进行比较.由实验数据可以看出LDOA-TS 算法在求解多目标有序用电用户组合问题上有较优的表现.
