堆浸体系内微细颗粒在孔隙内迁移和附着规律

2024-05-03唐惠阳尹升华

工程科学学报 2024年6期

陈威，唐惠阳，尹升华

1) 北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083 2) 北京科技大学土木与资源工程学院，北京 100083

堆浸是利用浸矿剂、浸矿微生物、催化剂等，选择性溶解矿石或矿体中有用金属矿，使金属由固态转换为液态再进行金属回收的采矿技术[1-3].由于堆浸生产简单、成本低和绿色等优点，以及它在回收低品位矿和难选矿等方面的优势，使得它在采矿业中得到了广泛使用[4-5].影响堆浸浸出效率的因素包括物理和化学两个方面，对于使用生物浸出的堆浸还需考虑生物因素[6].物理因素包括矿石的孔隙度、渗透性等；化学因素指浸矿液和矿石的化学性质以及两者之间发生的化学反应；生物因素则是指浸矿微生物的活性、数量以及其对矿物浸出的影响和作用机理等.

堆浸系统是一个由固、液、气三相组成的多相体系，它的骨架是由矿石颗粒组成的多孔介质[7].由于矿石颗粒的大小和形状各不相同，因此其孔隙网络结构非常复杂.早期实验经常将堆浸系统视为“黑箱”来研究其渗透特性，但随着科学技术的发展，多孔结构和矿物颗粒的分布可视化成为了可能，如X射线计算机断层扫描技术(CT)、磁共振成像技术(MRI)和粒子图像测速法（PIV）技术等[8-9].此外，一些图像处理算法的采用也显著提高了图像的清晰度[10-11].美国工程院院士Miller率先使用高分辨率X射线微型CT来测定有价值的矿物颗粒暴露率和估计多相颗粒的回收率[12].王文凤[13]对国内外使用CT技术研究散体孔隙结构的应用现状进行了总结，指出了CT技术研究堆浸散体所存在的问题，最后对该技术在溶浸采矿的应用前景进行了展望.但以上技术只能捕捉到浸出过程中的某个瞬间，为了进一步研究堆浸过程的动态发展，学者们开展了对溶浸过程的模拟仿真技术的研究[14].

要实现对溶浸过程的模拟仿真研究首先要建立堆浸系统的孔隙空间模型.孔隙模型的建立方法一般分为两大类.第一类是利用统计方法（如蒙特卡罗）对孔隙空间进行随机重构，但是该方法很难获得孔隙空间的分布参数，因此无法准确描述孔隙结构性质.第二类是利用各种扫描技术直接获取介质图像，再构建孔隙结构的几何模型[15].由于第二类方法是基于真实的矿石颗粒孔隙而建立的模型，因此其模型的性质和结构更为接近真实情况，也是更为常用的孔隙建模方法.X射线计算机断层扫描（CT）作为一种非侵入性技术，由于它拥有非常高的分辨率且能够扫描相对较大的样本，因此利用基于CT图像构建的真实孔隙网络模型进行模拟仿真实验逐渐成为普遍使用的方法[16].堆浸系统浸出过程模拟仿真的常用软件有Fluent、Comsol等，本实验则使用Fluent进行模拟实验.

堆浸系统中的孔隙是浸矿液流动扩散的通道，主要分为颗粒间孔隙和颗粒内孔隙[17].颗粒间孔隙的孔喉孔径一般为毫米级甚至厘米级，而颗粒内孔隙的孔喉孔径仅为微米级[18].在浸出过程中，随着浸矿液从矿堆顶部沿孔隙向下渗透，浸矿液会逐渐充填孔隙空间，当某一部位的孔隙完全被溶液填满而不存在空气时，则称该部位为饱和区反之则称为非饱和区[19].由于在堆浸系统中存在许多游离的颗粒，它们会随着溶液流动而发生迁移，且经常导致堵塞孔隙从而影响浸出速度和效率[20].在颗粒间孔隙内，当游离颗粒通过孔径小于其粒径的孔喉时则会形成堵塞；当孔隙较为平缓其内流体流速较慢时，较大颗粒可能在孔喉前堆积从而造成堵塞，而当几个较大颗粒同时通过孔喉时彼此之间相互作用可能会产生组拱堵塞现象[21-22].而对于粒径较小的微细颗粒，由于它们难以对颗粒间孔隙形成堵塞，因此对它们的迁移规律的研究较少.然而虽然它们对颗粒间孔隙内的溶液流动影响有限，但是当它们大量覆盖在孔隙壁表面时也可能会影响溶液浸入矿物颗粒内部，从而影响浸出效率.当微细颗粒停留在孔隙壁上时，微细颗粒与微细颗粒之间或微细颗粒与孔隙壁之间还可能产生物理化学反应而粘连在一起，如同一个密闭的膜，从而影响浸出效率.因此探究微细颗粒在孔隙内的迁移与附着规律具有重要意义.

对此本文立足于真实的孔隙结构，使用CT技术和Avizo软件从柱浸实验中获取真实的孔隙模型，结合Fluent meshing工具实现孔隙模型的网格划分，最后在Fluent平台开展微细颗粒在孔隙内迁移与附着行为的模拟仿真实验.本实验探究了粒径、颗粒密度和流体流速对微细颗粒运动轨迹的影响，通过控制变量对单一变量的不同实验结果做对比，结合颗粒的受力分析对实验现象做出解释.

1 孔隙模型的建立

1.1 假设

为了简化模拟实验，对实验做出以下假设：

(a) 该模型为饱和流模型，孔隙完全被溶液充满不会产生气泡，不考虑空气的影响；

(b) 本模型不考虑化学因素和侵蚀作用，孔隙壁不会产生形变和位移；

(d) 忽略生物因素的影响；

(e) 不考虑流体温度变化的影响，忽略毛细作用；

(f) 本实验为DPM模型，颗粒与颗粒之间不会相互作用，互不影响.

1.2 三维模型的建立和网格划分

实验所用矿石样品来自某铜矿，矿石颗粒放置在直径60 mm、长度540 mm的浸矿柱中.浸矿柱上部矿石颗粒粒径较大，粒径范围在10～20 mm，有利于微细颗粒向下迁移使得下部能聚积更多微细颗粒，而下部矿石颗粒粒径均小于5 mm，颗粒间孔隙较小、溶液流速慢，微细颗粒更容易附着.本实验使用nanoVoxel-4000型X射线三维扫描系统对浸矿柱进行CT扫描.它具有高穿透能力和高分辨率，其空间分辨率可达2 μm，可以满足实验中图像采集的要求.样品的其中一个CT扫描图如图1所示.

图1 CT扫描图Fig.1 CT scan

通过对CT扫描原图预处理可以减少噪点、模糊等不良影响.然后使用Avizo软件对处理后的CT图片进行三维重构从而得到浸矿柱的三维模型，最后从浸矿柱模型下部的小粒径矿石部位裁剪得到一个实际大小为11.1 mm×9.9 mm×7.4 mm的立方体.

将得到的模型导入Ansys Fluent Meshing网格划分工具对所获得的三维模型进行网格划分.本实验采用马赛克网格划分方法生成体网格，该划分方法能够提高网格中六面体网格占比的同时减少总网格数量从而提高网格质量.本模型共划分了313231个网格，如图2所示.

图2 网格划分Fig.2 Meshing

1.3 控制方程

由于堆浸系统中的孔隙曲率大、分支多、变化大且孔隙壁不规则，溶液在内流动时常处于紊流状态.而Fluent提供的SSTk-ω模型比较适用本实验的孔隙情况，因此选择该模型控制流体流动，其公式如式（1）～（5）所示[23]：

湍流动能k：

耗散率ω：

低雷诺数修正：

在高雷诺数时：

其中：Gk表示湍流动能，由平均速度梯度产生；ρ代表流体密度；Gω表示ω的生成；Γk和Γω分别代表k和ω的有效扩散系数;Yk和Yω表示k和ω在湍流作用下的耗散；σk和σω分别是k和ω的湍流普朗特数；μ代表流体的分子粘度；µt为湍流粘度；Ret表示湍流雷诺数；u表示流速；Sk和Sω是用户定义的源项；Gb和Gωb解释了k-ω模型中浮力对湍流的影响中所描述的浮力项.

对于颗粒在孔隙内的运动则通过在拉格朗日参考系下对离散相颗粒的力平衡做积分来预测离散相颗粒的运动轨迹，如式（6）所示.

其中：Re代表相对雷诺数；dp代表颗粒粒径.

由于离散相颗粒在流体中运动时可能会相对流体做加速运动，在这个过程中可能会产生附加力，该力被称为虚拟质量力，其表达式如式(9):

其中：Cvm代表虚拟质量因子，通常Cvm=0.5;为流体的速度梯度.

在模拟实验中，流体在孔道内流动时不同位置的流体中压强不同.而由于压强分布不均而形成的力被称为压力梯度力.其方向为从高压强区指向低压强区，表达式如式（10）：

虚拟质量力和压力梯度力只有当流体密度接近或超过颗粒质量时对颗粒的影响才显著.一般来说当流体密度ρ与颗粒密度ρp之比大于0.1就需要将这两个力纳入考虑.本实验的流体密度ρ=1000 kg·m-3，颗粒密度ρp≤10000 kg·m-3，因此本实验需要将虚拟质量力和压力梯度力纳入力平衡公式.

在流体流动过程中，在垂直于流体流动方向的孔隙横截面上，距离孔隙壁不同距离的流体流速不同从而形成速度梯度，当颗粒速度与流体流速存在差异且颗粒运动方向与流体的速度梯度垂直时，颗粒会受到流体的剪切作用.这种剪切作用会产生Saffman升力，升力方向为从低速方向指向高速方向，其表达式如式（11）[25-26]：

其中：K=2.594；dij为变形张量；v为流体速度；dlkdkl代表流体的高切应力参数.

Saffman升力只适用于亚微米颗粒，即粒径处于1×10-6～1×10-7m的小颗粒.本实验中部分实验的颗粒粒径处于微米级，因此需要考虑Saffman升力.

1.4 变量选取

颗粒在孔隙内迁移和堵塞行为相关的研究较多，部分学者还对颗粒堵塞类型进行了分类如依赖堵塞、独立堵塞、表层截留、内部阻塞和附着等[26-28].但其研究的对象主要为毫米级或亚毫米级的颗粒，忽略了更小粒径颗粒对浸出效率的影响.周凌波等[29]使用扫描电镜观察将浸出后的粘土颗粒表面放大1万倍后观察发现，粘土颗粒表面吸附了大量大小不同的细微颗粒，且颗粒之间相互粘结.而微细颗粒的大量附着可能影响浸矿液向孔隙壁内部的渗入，从而影响浸出效率.由于微米级以下的颗粒受力和运动轨迹较为复杂且对浸出影响较小因此本实验选择粒径10-6～10-4m的微细颗粒作为研究对象，探究微细颗粒在孔隙内的迁移和附着规律.

影响颗粒在孔隙内迁移和堵塞行为的因素有很多，如粒径比、渗流速度、粒径、孔隙结构等[30-31].本实验选择颗粒粒径、颗粒密度和流体流速（渗流流速）三个易于控制的变量进行实验.在实际浸出过程中，由于金属矿物颗粒含量相对较小，且容易在浸矿液中溶解，因此游离的颗粒大部分为非金属矿物颗粒.而非金属矿的密度主要处于1500～3500 kg·m-3之间，因此本实验所选用的微细颗粒的密度也在此范围之内.孔隙内溶液在孔隙内流动时受重力作用其动能会不断增加.但溶液在孔隙内流动时与孔隙壁之间的作用力又会损耗溶液动能，且流速越快能量损耗越多.所以，虽然孔隙内不同位置的溶液流速不同，但其流速仍处在一定范围之内.Alem等[32]曾以渗流流速为变量，发现低流速会促使颗粒在多孔介质表层产生沉积，高流速则会增大颗粒的堵塞深度，其渗流速度的范围为10-2～10-4m·s-1.本实验也采用与之相同的渗流流速.

该矿样的主要成分为惰性的SiO2，质量分数占比达到了91%，由此推测孔隙内的微细颗粒主要为SiO2颗粒.因此本实验在探究粒径和流体流速对颗粒迁移影响时均选用SiO2的密度即2200 kg·m-3的微细颗粒作为研究对象.

2 结果与讨论

2.1 颗粒轨迹与流体迹线对比分析

将入口初始流速为0.001 m·s-1的流体在孔隙内流动的迹线与粒径为1×10-5m、密度为2200 kg·m-3的微细颗粒在该流体内迁移的运动轨迹进行对比，为便于观察删减了部分重复路径，如图3所示.

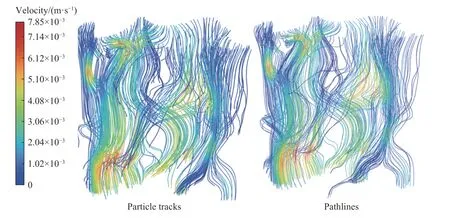
图3 颗粒轨迹（颗粒初始速度0.001 m·s-1，粒径 1×10-5 m，颗粒密度2200 kg·m-3）与流体迹线（流速0.001 m·s-1）Fig.3 Particle tracks (particle initial velocity of 0.001 m·s-1, particle size of 1×10-5 m, particle density of 2200 kg·m-3) and pathlines (flow velocity of 0.001 m·s-1)

由图可知流体迹线和颗粒的运动轨迹大致相当.刚流入孔隙的流体和微细颗粒的初速度速度相同，在经过孔喉时两者速度都会增大，经过孔喉后流体和微细颗粒的速度又都会迅速降低，但微细颗粒的速度减少量略小于流体.因此在经过孔喉后，微细颗粒的速度整体上会略大于流体流速.虽然由于密度更大，颗粒在竖直方向上运动速度较快，但从图中可知颗粒的速度并未显著超过流体.对其做受力分析可知，微细颗粒受恒定的重力，方向竖直向下.沿流体流动方向，当流体流速大于颗粒速度时，颗粒受流体的推力，当流体流速小于颗粒速度时，颗粒受到流体的阻力.流体的推力大小与颗粒密度和颗粒与流体的速度差呈正比.当颗粒相对流体做加速运动时会产生虚拟质量力，虚拟质量力的方向为加速度的反方向.因此当颗粒速度超过流体流速并相对流体继续加速时，颗粒受到的虚拟质量力会阻碍颗粒速度进一步增大，使得颗粒速度始终未能超出流体流速过多.

此外，由于颗粒的惯性相对较大，运动方向转变较为困难，因此在通过弯孔隙时颗粒会向外孔隙壁偏移，甚至与外孔隙壁发生接触而吸附在孔隙壁上不再移动.由图3也可以观察到颗粒运动轨迹的方向变化幅度较小，而流体迹线则更为弯曲.统计最终流出孔隙时的颗粒和流体的速度，如图4，流出孔隙时颗粒的平均速度为3.36×10-3m·s-1，而流体的平均速度仅为0.96×10-3m·s-1，颗粒平均速度明显大于流体平均速度.分析认为在近壁面运动的低速颗粒比在孔隙中心运动的高速颗粒更容易吸附在孔隙壁上，使得部分近壁低速颗粒没有流出孔隙.因此流出孔隙的颗粒中高速颗粒占比较大，平均速度也更大，而流体则不存在这一现象.

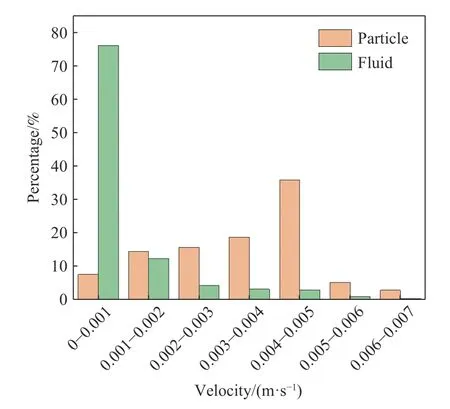
图4 流出孔隙时流体和颗粒的速度分布Fig.4 Velocity distribution of fluid and particles as they exit the pores

2.2 颗粒粒径对颗粒运动轨迹的影响分析

本组实验的流体在孔隙入口时的初始流速为0.001 m·s-1，微细颗粒密度为2200 kg·m-3.微细颗粒粒径分别为1×10-6、5×10-6、9×10-6、1×10-5、2×10-5、3×10-5、5×10-5、7×10-5、9×10-5m.不同粒径的颗粒轨迹对比图如图5所示.

图5 粒径影响下的颗粒轨迹对比Fig.5 Comparison of particle trajectories under the influence of particle size

在孔隙内，受重力影响，微细颗粒大多集中在孔道的下半部分迁移.而大孔隙联通着一些小分路孔隙，由于其入口位置位于大孔隙壁的中上部位且其内流体流速较慢，因此微细颗粒难以流入其中.对不同粒径颗粒的颗粒轨迹进行对比可以发现，当颗粒粒径为0.001 mm时有少量颗粒进入图中框选的两处小分路孔隙中，但当颗粒粒径为0.01 mm时则没有颗粒进入该小分路孔隙.且这一类小分路孔隙入口位置越高、孔径越小，流入的微细颗粒数量越少.观察发现，随着颗粒粒径的增加，颗粒会逐渐集中在大孔径、高流速的孔隙内迁移，在低流速、小孔径的孔隙内的颗粒数量会逐渐减少.

统计不同颗粒粒径附着的微细颗粒数量占总数量的百分比，并绘成曲线图，如图6黑色曲线所示.由曲线图可知，当粒径为1×10-6m时微细颗粒几乎不会附着在孔隙壁上，微细颗粒能够完全从孔隙内流出.随着颗粒粒径的增大，附着在孔隙内部未能流出孔隙的微细颗粒数量逐渐增多，在粒径为6×10-5m左右时达到峰值.其附着颗粒数占比达到了90%以上.随着颗粒粒径继续增加，颗粒附着数量开始减少，呈下降趋势.观察微细颗粒的附着位置可以发现，微细颗粒除了附着在孔隙壁较为平缓，流体流速较小的位置，如缓倾斜的小孔隙内，在某些“急转弯”孔隙处的外壁也有大量颗粒附着.随着粒径的增大微细颗粒在弯孔隙处的附着数量增大，进入小孔隙内的颗粒数量减少.但当微细颗粒粒径超过某一值后，微细颗粒接触到倾斜孔隙壁后不会附着在上面，反而会沿壁下滑.对不同粒径颗粒的运动轨迹进行对比发现，当颗粒粒径到达9×10-5m时，在急倾斜孔隙中，微细颗粒的运动轨迹甚至近似于竖直下沉，颗粒的水平运动幅度很小.此外，在同一孔隙内，靠近孔隙壁的微细颗粒的运动速度远小于在孔隙中心部位微细颗粒的运动速度.且当颗粒与孔隙壁接触后容易吸附在孔隙壁不会再返回流体中随流体继续迁移.

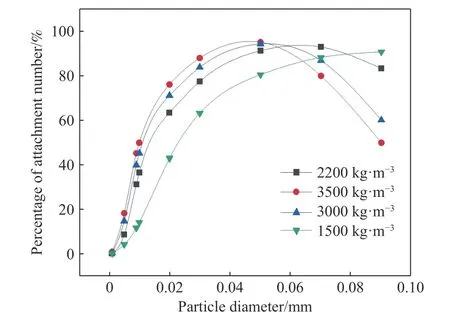
图6 颗粒粒径与附着数量百分比关系曲线Fig.6 Relationship between particle size and percentage of attachment number

对颗粒进行受力分析可知，当颗粒粒径小于1×10-5m时，颗粒受重力影响较小，受流体的作用力相对更大.此时颗粒受Saffman升力影响较大，而该升力方向是从孔隙壁指向孔隙中心，它会阻碍颗粒靠近孔隙壁.此外由于孔隙中心和孔隙壁处的流体流速不同形成了压力差，当颗粒向孔隙壁运动时还会受到压力梯度力的作用，该作用力的方向也是从孔隙壁指向孔隙中心.因此颗粒很少与孔隙壁接触也很少会附着在孔隙壁上，即使与孔隙壁接触也会在流体的作用下继续迁移.但随着颗粒粒径增大，颗粒受重力影响变大受流体影响相对减小，更容易在迁移过程中与孔隙壁发生碰撞从而停留在孔隙壁上.而此时流体的推力又不足以推动颗粒克服摩擦继续迁移，所以附着颗粒数会随着颗粒粒径的增大而增多.这与其他学者关于粒径对悬浮颗粒迁移沉积特性的研究结果一致[33].统计流出孔隙时颗粒的速度分布，如图7所示，小粒径颗粒中的低速颗粒占比明显多于大粒径颗粒中的低速颗粒占比，高速颗粒占比则恰好相反.且粒径为0.005、0.01、0.02、0.03、0.04和0.05 mm的颗粒，流出孔隙时的平均流速分别为3.21×10-3、3.36×10-3、3.63×10-3、3.97×10-3、4.35×10-3和4.89×10-3m·s-1，平均速度不断增大.分析认为随着粒径的增大，低流速的颗粒更容易吸附在孔隙内，使得最终流出孔隙的颗粒中高速颗粒占比更大，其平均流速也就更大.

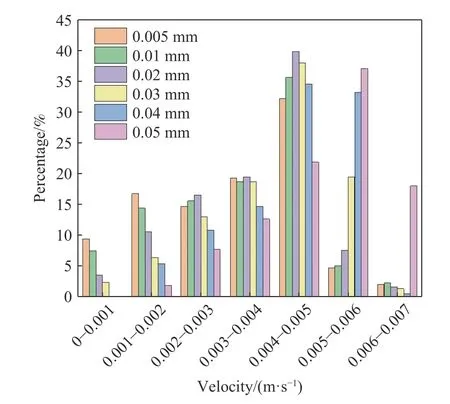
图7 流出孔隙时不同粒径颗粒的速度分布Fig.7 Velocity distribution of particles with different sizes during outflow from pores

随着颗粒粒径继续增大，在倾斜孔壁上的吸附能力变弱，颗粒受重力和惯性的影响也增大.当大粒径颗粒与倾斜孔隙壁接触后，更容易在重力和惯性以及流体的作用下岩壁下滑从而使得吸附在孔隙壁上的的颗粒数量随着粒径的增加而减小.本实验未考虑颗粒间的相互作用，因此不会产生堆积堵塞的现象.但由于此时孔隙孔径远大于微细颗粒的粒径，即使颗粒在孔隙内堆积也难以堵塞颗粒间孔隙，颗粒最终会在渗流作用下进一步向下迁移[30].

2.3 颗粒密度对颗粒运动轨迹的影响分析

本组实验流体在孔隙入口的初始流速为0.001 m·s-1，颗粒密度分别为1500、3000、3500 kg·m-3，重复上组实验.分别记录不同颗粒密度的实验中附着的微细颗粒数量占总数量的百分比，并绘制与颗粒粒径之间的关系曲线，如图6所示.由曲线图可知，对于不同密度的微细颗粒，其附着颗粒数百分比与颗粒粒径的关系曲线相似，附着颗粒数量随着颗粒粒径的增加先增大后减小.由图6可以发现峰值前，粒径相同时，微细颗粒的密度越大，颗粒附着比例越大，如粒径为0.01 mm时，1500 kg·m-3的颗粒附着比例仅为14.33%，而密度为3500 kg·m-3的颗粒附着比例则增大至49.86%.且颗粒密度越大曲线峰值所处的颗粒粒径越小，颗粒密度为3500 kg·m-3时峰值粒径约为0.05 mm，而颗粒密度为1500 kg·m-3时峰值粒径约为0.09 mm.

对比峰值前不同密度相同粒径微细颗粒的轨迹图，如图8.颗粒密度越大，颗粒在弯孔隙处附着颗粒数明显增多.如图9，流出孔隙时小密度颗粒的低速颗粒数量占比大于大密度颗粒，而高速颗粒数量占比则相反.小密度颗粒流出孔隙时的平均速度为3.25×10-3m·s-1，小于大密度颗粒的平均速度3.47×10-3m·s-1.由此可知微细颗粒密度越大，流出孔隙的颗粒中高速度颗粒占比越大.

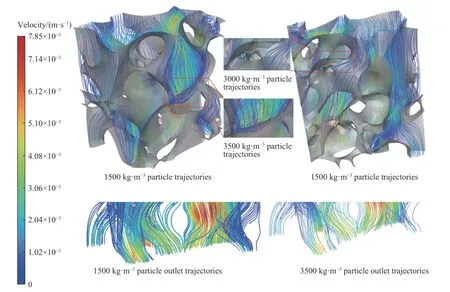
图8 颗粒密度影响的颗粒轨迹对比Fig.8 Comparison of particle trajectories under the influence of particle density

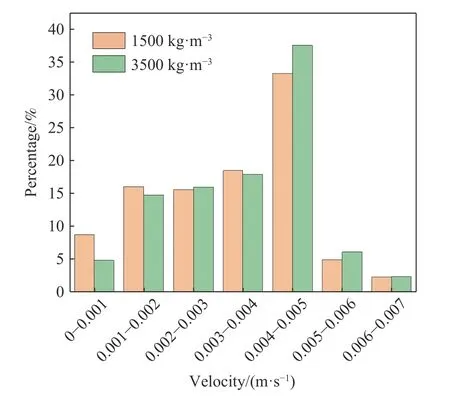
图9 流出孔隙时不同密度颗粒的速度分布Fig.9 Velocity distribution of particles with different densities during outflow from pores

根据前人的研究成果，重力越大，流体的水动力作用对颗粒迁移轨迹的影响越小[34].粒径相同时，颗粒密度越大，颗粒受重力和惯性的影响越大，而流体对颗粒的作用力不变.因此大密度颗粒更容易在平缓孔隙和弯孔隙处与孔隙壁发生接触，从而吸附在孔隙壁上.而靠近孔隙壁的颗粒，由于其流速慢且靠近孔隙壁，在迁移过程中更易于接触并吸附在孔隙壁上，使得最终流出孔隙的颗粒中远离孔隙壁的高速颗粒占比更大.

2.4 流体流速对颗粒运动轨迹的影响分析

本组实验选取颗粒密度为2200 kg·m-3，颗粒粒径为1×10-5m，流体初始流速为0.005 m·s-1，如图10所示.此流速下附着颗粒数仅占7.86%，而初始流速为0.001 m·s-1时附着颗粒数占36.64%.很明显，提高流体流速，颗粒的附着数量明显减少.将该图与图3进行对比，发现在高流体流速时，颗粒的运动速度更快，在水平方向的运动幅度明显增加，颗粒轨迹更加分散，在孔隙中心和上部运动的颗粒更多，进入小分路孔隙的颗粒也更多.这与渗流速度对颗粒沉积影响的相关研究结果相符.渗流速度越大，水动力作用对颗粒的影响越大，沉积系数越小，颗粒越不容易产生沉积，颗粒的弥散效果更好[35-36].由此可见，适当提高渗流速度可以减轻微细颗粒的附着现象，减少微细颗粒的附着对浸出效率的影响

图10 颗粒轨迹(颗粒初始速度0.005 m·s-1, 粒径1×10-5 m, 颗粒密度2200 kg·m-3)Fig.10 Particle tracks (particle initial velocity of 0.005 m·s-1, particle size of 1×10-5 m, particle density of 2200 kg·m-3)