低效井合理捞油周期确定方法研究

王瑞 蔡文斌

（1.西安石油大学石油工程学院；2.中国石油长庆油田分公司第十采油厂）

位于鄂尔多斯盆地的华庆油田属于典型的“三低”油气藏，具有低压、低渗、低丰度特点[1]。随着开发的不断深入部分区块已进入中后期开发阶段。低产低效井、偏远长停井数量逐年增加，这些井地层压力低、生产压差小、动液面恢复慢，按照常规的有杆采油方式生产成本较高[2]。针对此类低产低效井，为了最大限度提高油井利用率，普遍采用提捞采油方式，同时针对捞油周期的确定也需进行研究。郭永贵[3]依托矿场数据统计，提出了一个经验公式，给出了有试井资料的提捞井捞油周期。于士泉、王永卓等[4]提出了一种计算油井提捞采油经济极限产能的计算模型，该模型为大庆外围油田提捞采油工作提供了有效、可行的评价基础依据。伊岚[5]结合压力恢复理论、技术经济分析，提出一种确定合理捞油周期的方法。李杨[6]在对兴茂采油作业区现场提捞作业调研后提出降低井筒储集，增强提捞效率的捞油周期确定方法。基于油井流入动态理论研究，结合井筒压力计算方程，建立一套捞油周期数学模型，优先对14 口捞油井进行试验，并且根据不同动液面上升速度、计算最佳捞油周期，同时结合现场动力情况对提捞井进行分类，形成了“以目标产量为导向、油量增速拐点为依据、高产短周期单捞，低产长周期合捞提效率”的捞油周期的确定方法，为后期规模推广应用提供参考依据。

1 研究思路与方法

捞油采油工艺是用钢丝绳将捞油泵从套管内下入井下套管或油管内，在下井过程中水力密封装置接触液面后沿中心管向上滑动，中心管底部侧孔道露出，井筒流体经侧孔道从密封装置上部溢出，当下行到预定深度后，上提中心管，由于液压作用，密封装备下行至中心管底部，封闭中心管底部侧孔，即可将上部液体举升到地面[7]。而对于提捞采油生产，合理捞油周期的确定尤为关键。周期较长造成储层潜力无法发挥，周期较短造成单次捞油量过低而浪费成本。该区捞油井所处油藏驱动方式为溶解气驱，由于井底流压普遍小于油藏饱和压力，所以井底流入动态符合油气两相渗流时的流入动态。计算模型思路见图1。

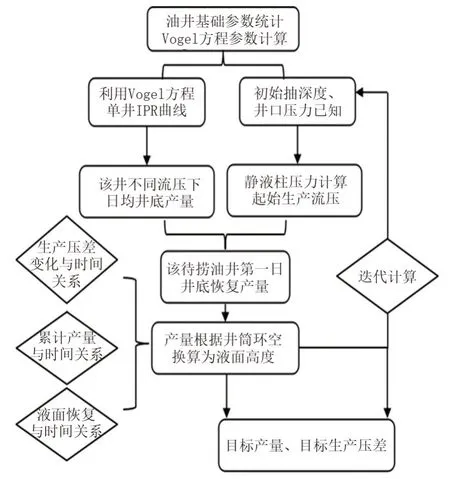
图1 计算模型思路Fig.1 Thinking of calculation model

Vogel 方程适用于溶解气驱油藏的无因次IPR 曲线描述，所以使用Vogel 方程计算理想完善井以及Standing 方法计算实际生产中不完善井的IPR 曲线，可直观得到不同流压下油井日产量。由于每次捞油抽深已知，则通过井筒压力方程计算出初始井底流压，并通过井底流压计算出该捞油井当日产量，再折算为动液面上升高度，计算出下一日起始井底流压；依次迭代计算每日产量、累积产量，再根据生产压差、累计液量、动液面恢复与时间的关系确定最佳周期。

1.1 IPR 曲线计算方法

已知油藏平均压力pr，以及对应的某一个测试产量qtest的流压pwf(test)，应用Vogel 方程计算IPR曲线步骤[8]，首先计算出q0max：

式中：qomax为流压为零时的最大产量，m3/d；q(test)为相应测试流压下的油井产量，m3/d；qoz、qox分别为直井和斜的油井产量，m3/d；pwf(test)为测试流压，MPa；pwf为井底流压，MPa；pr为平均地层压力，MPa。

计算不同流压下井底日产量，公式（2）适用于直井计算，值得注意的是Vogel 方程适用于直井油气两相流入动态计算。对于斜井IPR 曲线计算，需要使用Vogel 回归经验方程公式（3）计算，其中A、B、C为井斜角系数（表1）[9]，最后根据公式（2）、（3）计算结果绘制井底流入动态IPR 曲线。

表1 Vogel 回归方程斜角系数Tab.1 Oblique angle coefficient of Vogel regression equation

采用Vogel 方程在计算无因次流入动态曲线时，认为油井是理想完善井，但实际情况油井并非理想的完善井。文中使用Stanging 方法计算非完善井的IPR 曲线，实际油井的完善性可以用流动效率ηPF来表示，如公式（4）、公式（5）所示，其中表皮系数S由压力恢复曲线测得。流动效率ηPE=1 为理想完善井，流动效率ηPE＞1 为措施后超完善井，流动效率ηPE＜1 为不完善井。当ηPE≠1 时也可利用Vogel 方程计算，但需要将其中流动压力用理想完善井的流压p′wf代替原Vogel 方程中的pwf[10]。计算方法为：①根据已知的-pr及pwf，计算在ηPE=1 时的产量，得到qomax(PE=1)，如公式（6）、公式（7）所示；②根据该井ηPE计算不同pwf对应的p′wf；③根据公式（8）求得相应产量。

式中：p′wf为理想完善井的流压，MPa； Δpsk为非完善井表皮附加压降，MPa；μo为地层原油黏度，mPa·s；Bo为原油体积系数；k0为油层有效渗透率， μm2；h为油层有效厚度，m；S为表皮系数。

1.2 产量预测方法

捞油井初次抽深已知，即可以依据井筒压力方程公式（9）近似计算出当日井底流压，再依据公式（3）、（8）计算得出当日产量。将当日产量根据公式（10）折算为动液面上升高度，得到第二天动液面深度，进而根据公式（9）求出第二天平均生成流压，再根据公式（3）、（8） 计算出第二天产量，根据此方法依次迭代计算得出生产压差、累积产量、动液面恢复与生产时间的关系。

式中：p套为套压，MPa；ρ油为原油密度，g/cm3；ρ水为地层水密度，g/cm3；fw为含水率，%；g为重力系数，9.8 N/Kg；r为井筒半径，m；h1为油层中深，m；h2为动液面高度，m；q为油井日产量，m3。

2 实际生产拟合对比

2.1 白61 井液量恢复计算

选择白61 井进行捞油周期理论实验计算（表2），并且根据现场实际捞油情况拟合计算准确性。已知白61 井油层中深2 376.2 m，抽深2 100 m。该井未进行试井测试，所以测试流压、测试产量选用正常机采时且动液面稳定条件下流压与日产量，符合溶解气驱油藏曲线特征。再根据上述产量预测方法，计算出qomax值为1.32 m3/d，并可计算出生产压差、累积产量、动液面恢复与生产时间的关系。

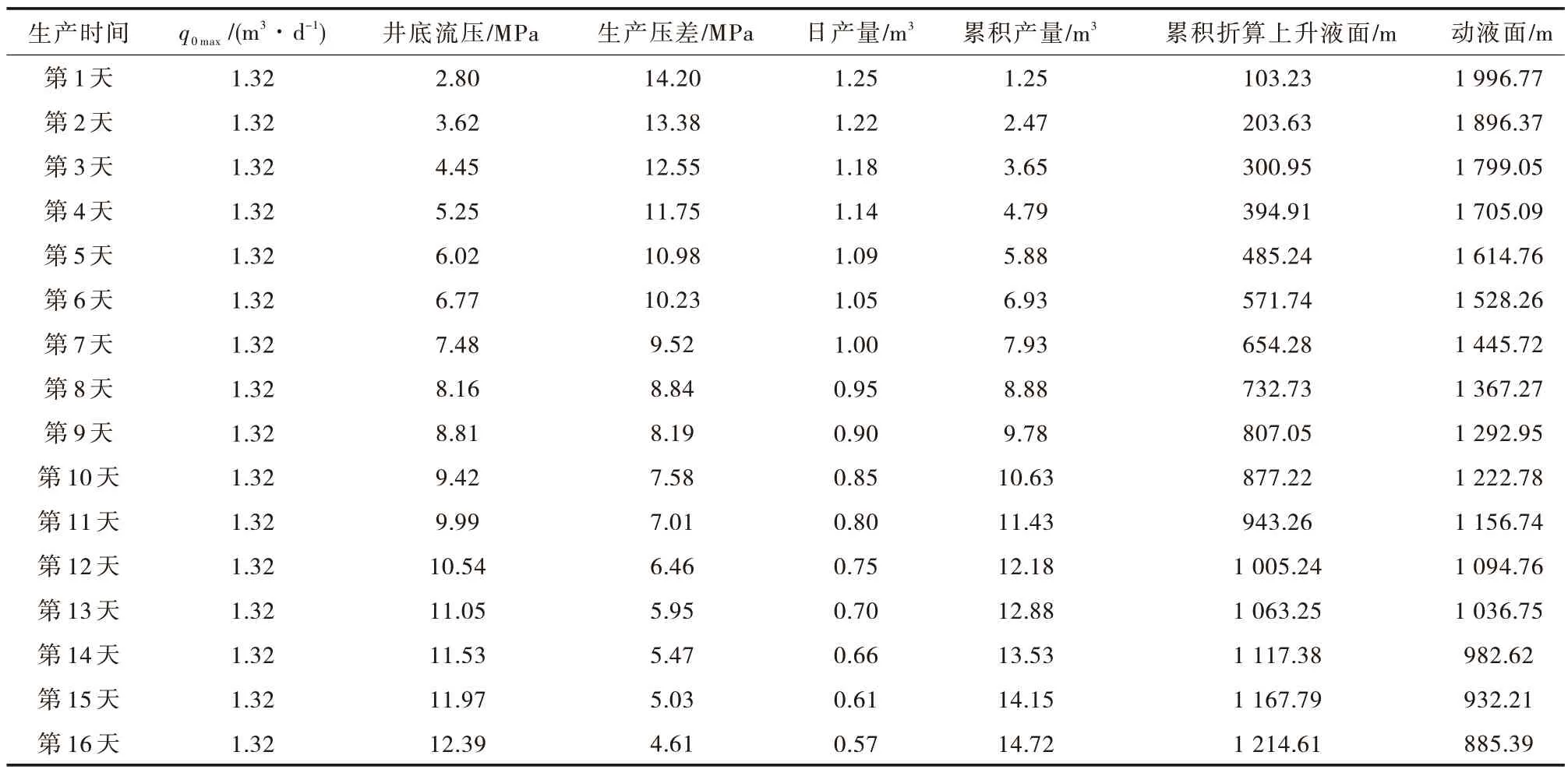
表2 白61 井产能恢复数据Tab.2 Productivity recovery data of Bai 61 well

2.2 白61 井实际捞油量与计算模型拟合

实际捞油与模型计算对比见表3，计算产量与实捞液量拟合曲线见图2。相同储备天数内，数学模型计算与实际捞油量平均误差为-0.12 t（小于1 t），表明该数学模型基本可以为现场作业提供参考。

表3 实际捞油与模型计算对比Tab.3 Comparison between actual bailing oil and model calculation

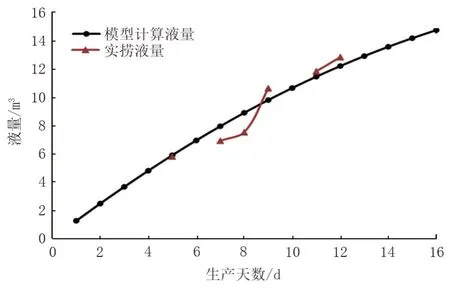
图2 计算液量与实捞液量拟合曲线Fig.2 Fitting curve of calculated liquid volume model and actual liquid volume

2.3 白61 井各参数关系分析

绘制白61 井理论计算累积产量、生产压差、动液面恢复高度与生产时间T关系曲线（图3），切线斜率代表其变化速度。可清楚地发现白61 井在初次捞油后，动液面恢复的前期由于生产压差的放大，动液面、液量恢复速度较快且恢复速度持续处于较高水平。而随着动液面的不断恢复，生产压差的不断减小，日产量不断的降低。动液面恢复高度、累积恢复液量与生产时间的关系的切线斜率均明显出现拐点，均在第11 天，即日产液量、动液面恢复速度在第11 天开始明显放缓。通过生产压差与生产时间的关系曲线可看出拐点也出现在第11天，生产压差变化幅度持续变小，切线斜率急速变小，生产压差趋于稳定，表明井底进入持续稳定的低产期。对于捞油井生产来说即需要尽快捞油，恢复较高生产压差而进入下一个生产周期，此变化节点即为捞油周期。

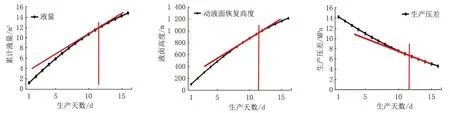
图3 白61 井理论计算累积产量、动液面恢复高度、生产压差与生产时间关系曲线Fig.3 Relationship between cumulative production，liquid level recovery height，production pressure difference and production time based on the theory calculation of Bai 61 well

3 推广应用

3.1 液量、油量恢复计算

白61 井模型计算结果与现场实捞情况拟合对比误差较小，故将此方法推广至另外13 口捞油井，计算出液量恢复与生产时间的关系，再折算油量恢复与生产时间的关系。捞油井底累积液量计算见图4。

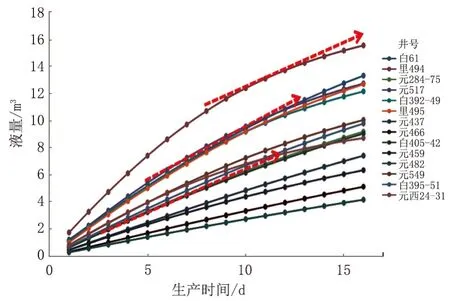
图4 捞油井底累积液量计算Fig.4 Accumulated liquid volume at the bottom of bailing well

通过14 口捞油井液量恢复曲线，不难发现各井井底产量增速差异较大，且随着井底流压的增高，产量增速拐点也存在差异。物性较好、原始地层压力保持较高的井产量增速快且增速拐点周期长，如里494 井第11 天产量增速减慢；原始地层压力保持一般的井如白61 井、里495 井产量增速拐点在第8 天减慢；原始地层压力保持较低的井，物性较差，如元482 井、元西24-31 井产量增速拐点在第5 天减慢。总体结果显示累积油量增速拐点大部分集中分部在第5 天、第8 天、第10 天。

3.2 捞油周期确定

理论上讲为获得最大捞油量，捞油作业时间点应该选择在每口井液量增速拐点时期进行捞油作业，使井底始终保持较低流压生产。但综合考虑井位、捞油作业综合成本，以“综合收益为导向、油量增速拐点为依据、高产井短周期单独捞油，低产井长周期合并捞油”思路确定捞油周期更加贴合实际生产。故以1 个月为作业周期，将捞油井划分为三类：Ⅰ类井油量恢复较快以10 d 为一个捞油周期；Ⅱ类井以15 d 为一个周期；三类井由于含水率较高、地层压力保持水平较低等因素，15 d 恢复油量在5 m3以下，取1 个月为1 个周期，进行多井合捞作业。根据此标准对14 口捞油井进行分类计算，Ⅰ类井5 口、Ⅱ类井5 口、Ⅲ类井4 口，实际每月作业26 次，平均单次作业捞油量5.2 t，预计捞油136.7 t（表4）。

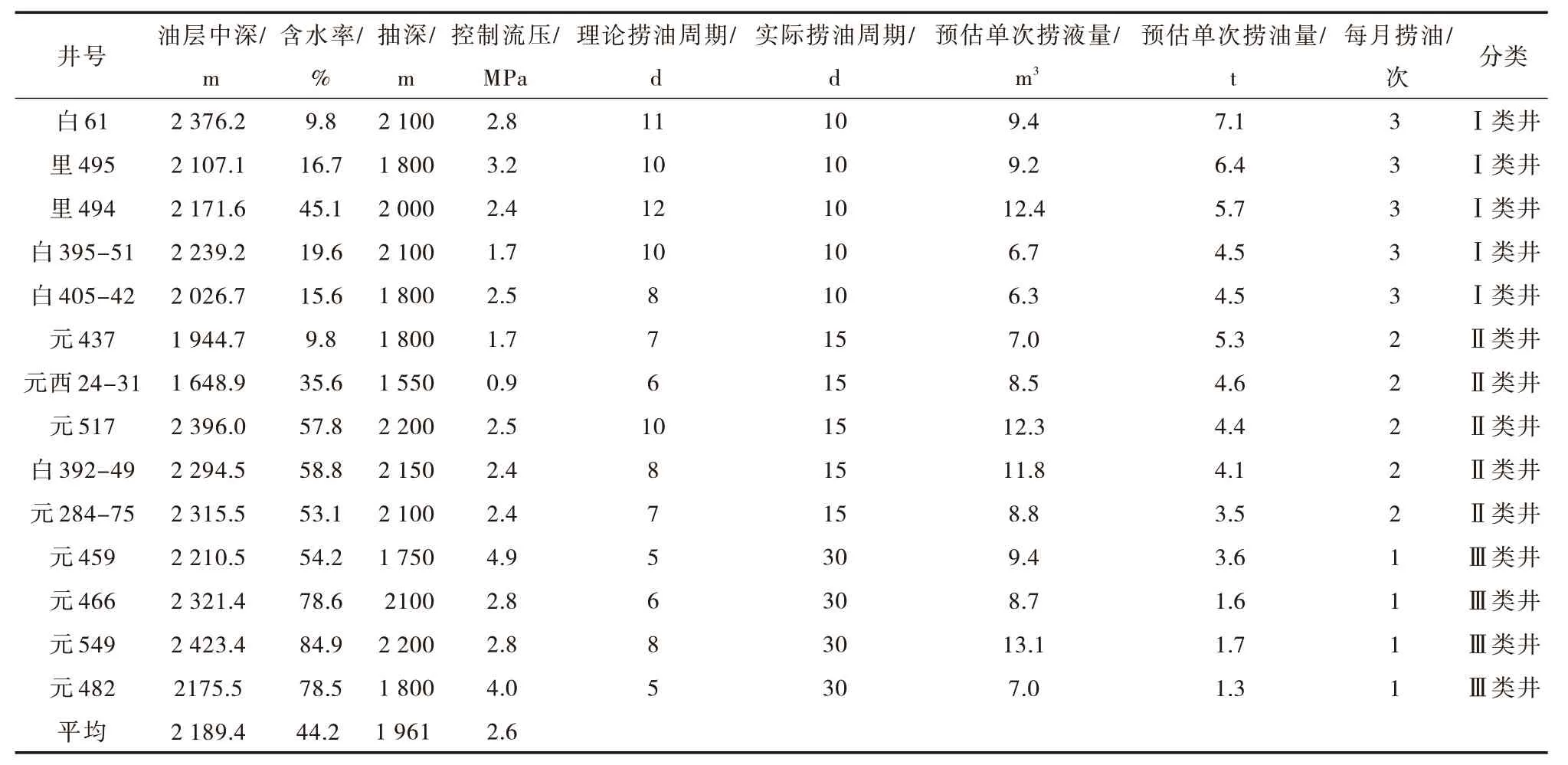
表4 捞油井捞油周期划分Tab.4 Division of bailing oil period for bailing wells

3.3 应用效果分析

HQ 作业区分月捞油情况统计见图5。2022 年8月、9 月开展笼统捞油，10 月、11 月逐步优化数学模型并按照计算周期安排作业，平均单次捞油量稳步上升。2023 年3—5 月，根据模型预测结果全面开展捞油作业，共计作业75次，捞获油量406.9 t，平均月捞油量135.6 t，单次作业5.4 t，与模型计算作业26 次，油量136.7 t，单次作业5.2 t 相当，分月对比月捞油量大幅提升，单次作业捞油量稳步增长（3.0 t 上升至5.4 t），取得显著效果。

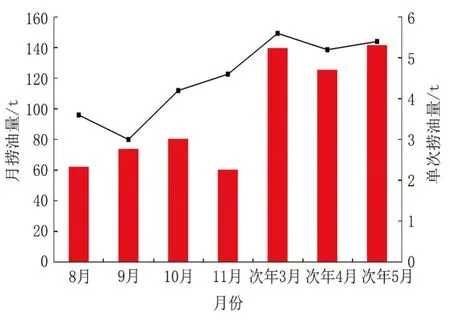
图5 HQ 作业区分月捞油情况统计Fig.5 Statistics of bailing oil per month in HQ operating area

4 经济效益评价

通过模型计算并结合现场作业综合成本，对捞油井周期进行具体分类合理安排捞油作业，2023 年3—5 月（全面应用该方法后）相对2022 年8—11 月（笼统作业），效率得到大幅提升。以每月计划作业25 次计算，笼统捞油平均单次作业3.4 t，平均月捞油量84.5 t，月综合收益24.71 万元。全面应用模型后平均单次作业5.4 t，月捞油量135.8 t，月综合收益40.8 万元。月捞油量上升51.3 t，月综合收益上升16.09 万元。

5 结论

1）靠矿场统计推断捞油周期，计算周期长且不准，易造成产量或者动力成本浪费。通过计算捞油井IPR 曲线，迭代计算井底流压，预测捞油井液量恢复情况，该方法误差在1 t 以内，各类参数简单易获取，可直接用于实际计算生产中。

2）该模型中累积液量与生产时间曲线变化率拐点为最佳捞油周期，但实际生产执行中要综合考单次作业综合成本，以“目标产量为导向、油量增速拐点为依据、高产短周期单捞，低产长周期合捞提效率”思路定周期，更有利于实现经济效益最大化。