一种自适应稀疏度的混合场信道估计算法
2024-04-30王华华龚自豪蒋天宇
王华华,龚自豪,蒋天宇
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
第六代(6G)移动网络有望赋能新兴应用,如全息视频、数字复制品等。为了实现这些愿景,需要开发新的无线技术,以满足6G的关键性能指标,而这些指标远优于5G[1]。例如,由于巨大的空间复用和波束赋形增益,超大规模多输入多输出(Extremely Large-scale Multiple-Input Multiple-Output,XL-MIMO)系统有望将6G的频谱效率提高10倍[2]。
与5G的大规模MIMO不同,6G的XL-MIMO不仅意味着天线数量的急剧增加,而且会导致电磁辐射特性的根本变化[3]。XL-MIMO中的电磁辐射可以分为近场辐射和远场辐射,不同辐射区域中散射分量的信道特性不同。文献[4]提出了瑞利(Rayleigh)距离作为两场的界限:若散射体离基站的距离大于Rayleigh距离则为远场区域,远场区域中的信道可以采用类平面波进行模拟建模;若散射体离基站的距离小于Rayleigh距离则为近场区域,近场区域中的信道则采用类球面波进行模拟建模。因此,XL-MIMO系统的混合场信道估计方案需要同时考虑近场信道分量和远场信道分量。
对于远场信道,通常考虑角度域中的信道稀疏性来进行信道估计[5]。远场信道的阵列导向矢量仅与每根天线的角度相关,因此可以借助于经典的离散傅里叶变换(Discrete Fourier Transform,DFT)矩阵在角域中将远场信道进行稀疏表示,然后通过一些压缩感知(Compressed Sensing,CS)算法用较低的导频开销来估计信道[6]。对于近场信道,信道的阵列导向矢量不仅与角度有关还与基站和散射体之间的距离有关,因此经典的角域信道表达式已不再适用。文献[7]提出了近场信道的极域稀疏表示,通过联合角度和距离生成变换矩阵,以取代仅与角度有关的经典DFT矩阵。通过考虑近场信道在极域中的稀疏性,可以采用一些CS算法来进行信道估计[8]。
然而上述工作仅适用于远场信道或者近场信道,很难扩展到同时具有远场路径分量和近场路径分量的XL-MIMO混合场信道场景。文献[8]根据远场路径分量的角域稀疏和近场路径分量极域稀疏性,采用正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法连续估计混合场信道的远场信道和近场信道分量。在此基础上,为了提高原子选择效率,文献[9]采用了广义正交匹配追踪(Generalized OMP,GOMP)算法对混合场信道进行估计。
以上方法虽然可以对混合场进行信道估计,然而均需要知道信道的稀疏度,但在实际应用中信道稀疏度往往是未知的[10]。本文利用不需要知道稀疏度的分段弱正交匹配追踪(Stagewise Weak Orthogonal Matching Pursuit,SWOMP)算法,与混合场(Hybrid Field,HF)信道相结合,提出了一种基于混合场信道估计的HF-SWOMP算法,以期实现未知稀疏度的XL-MIMO混合场信道估计。
1 系统模型
图1为一种工作在时分双工(Time Division Duplexing,TDD)模型下的下行链路混合场通信系统模型,基站采用N单元超大规模天线阵列与单个天线用户通信。
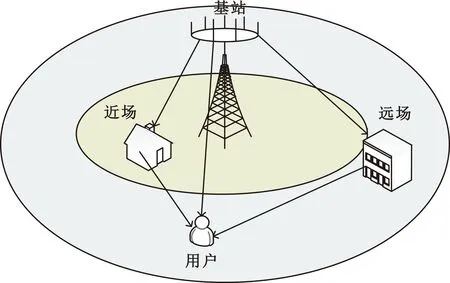
图1 混合场通信系统模型Fig.1 Hybrid-field communication system model
1.1 信号模型
用hH∈1×N表示从基站到用户的信道,则相应的信号模型可以表示为
yH=hHPH+nH
(1)
式中:yH∈1×M表示用户在M个时隙中接收到的导频信号;PH∈N×M代表基站在M个时隙内传送的导频信号;n~CN(0,σ2IM)表示用户在M个时隙中接收到的噪声信号。
通过转置,公式(1)可以变化为
y=Ph+n
(2)
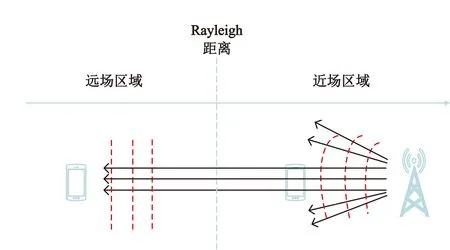
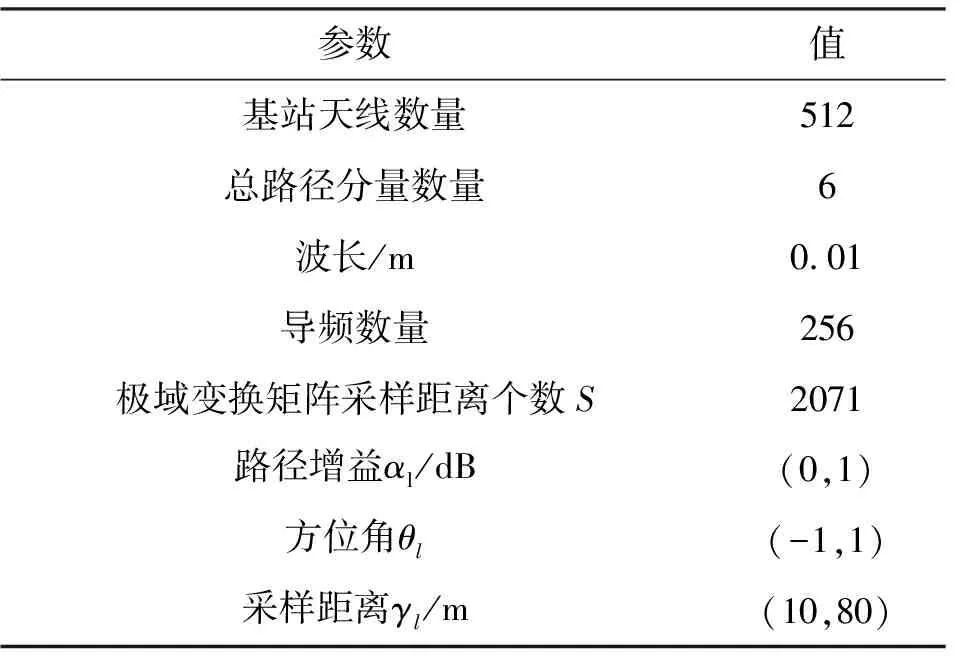
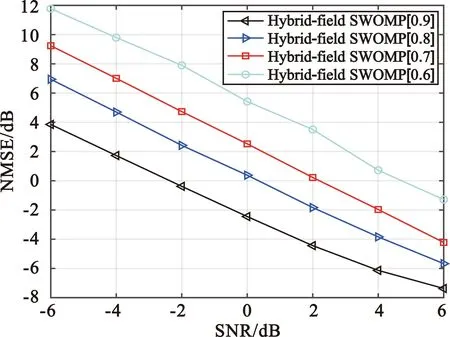
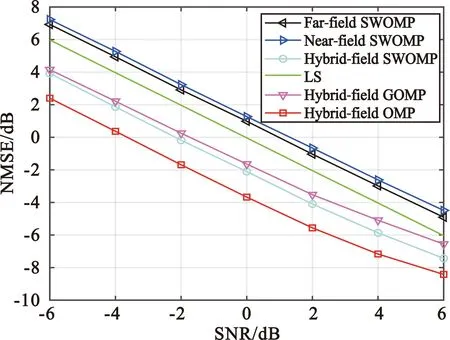
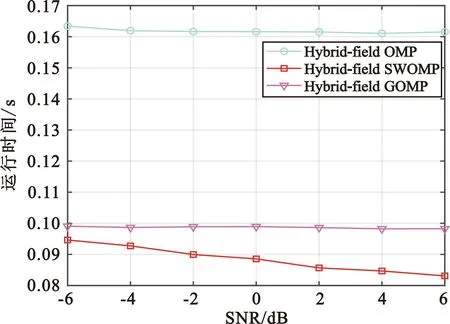
在混合场信道模型中,信道h∈N×1由远场路径分量hF∈N×1(d>D)和近场路径分量hN∈N×1(d y=PhF+PhN+n (3) 由图1和公式(3)和可以看出,XL-MIMO混合场系统中的电磁辐射分为近场辐射和远场辐射[5],如图2所示,不同场辐射区域的电磁波特性不同,近场和远场辐射之间的界限由Rayleigh距离D决定,Rayleigh距离D可表示为 (4) 图2 近场和远场区辐射Fig.2 Near-field and far-field area radiation 式中:R为天线阵列孔径;λ为波长。 1.2.1 远场信道模型 当散射体离基站的距离大于Rayleigh距离,信道可被视为远场信道,因此信道基于平面波前进行建模,远场信道hF可以表示为 (5) 式中:L和LF分别表示混合场路径分量的数量和远场路径分量的数量;βlf和φlf分别表示远场第lf条路径分量的复增益和方位角;a(φlf)∈N×1表示远场阵列导向矢量,可表示为 (6) 由于基站通常放置在距离有限散射体的较高位置,因此远场路径分量在角度域中显示出稀疏性。远场路径分量hF可以用系数角度域路径分量hf和离散傅里叶变换矩阵的乘积来描述: hF=Uhf (7) 1.2.2 近场信道模型 另一方面,当散射体离基站距离小于瑞利距离时,信道被视为近场信道,因此可以基于球面波前进行建模,近场信道hN可以表示为 (8) 假设第n条天线坐标为(0,δnd),δn=(2n-N+1)/2,n=0,1,2…,N-1,θ1∈[-1,1]表示空间角度,利用几何学从图3可得[11] (9) (10) 从公式(9)和(10)可知,近场信道模型的转向矢量b(θl,rl)不仅仅与元素的相位有关,还与离散射体的距离有关。因此,近场信道模型的转向矢量不是Fourier矢量,不再适用于远场信道模型下的Fourier矢量。 基于球面波建模的近场阵列导向矢量b(θl,rl)为 (11) 由于式(6)中与角度域相关的DFT矩阵仅匹配远场中的阵列引导向量,因此式(8)中的近场信道将在角度域中引起严重的能量扩散。文献[4]提出了近场信道的极域变换矩阵,可以将近场信道在极域中进行稀疏化。变换矩阵W可表示为 W=[b(θ1,r11),…,b(θ1,r1s1),…, (12) hN=Whn (13) 式中:hn是S×1维的极域信道,该信道与角度域表示的远场信道类似,也体现出稀疏性。 1.2.3 混合信道模型 在XL-MIMO系统中既包含近场信道分量又包含远场信道分量,因此仅用近场信道模型或者仅用远场信道模型均无法准确表示XL-MIMO信道模型。结合近场和远场信道模型,本节提出一种XL-MIMO混合场通信信道模型。 根据XL-MIMO混合通信模型中存在的两种不同类型的散射体,结合近场和远场信道模型的特点,混合场信道数学模型可以表示为 (14) 式中:L表示XL-MIMO混合场信道中的所有路径分量的数量;γ∈[0,1]表示可变参数,可以控制两种场的路径分量的比例,γL为远场路径分量的数量,(1-γ)L为近场路径分量的数量。从上式可以看出,当γ=0时,信道中仅含近场路径分量,混合场信道模型可视为近场信道模型;反之当γ=1时,信道中仅含远场路径分量,混合场信道模型可视为远场信道模型。因此,现有的单一远场和近场信道模型都是混合场信道模型中的特殊情况[12]。 由于在混合信道中有近场和远场两种不同的路径分量,因此会对应不同的CS估计的问题。将式(13)和式(7)代入式(3)中,式(3)可以重写为 y=PhF+PhN+n=PFhf+PWhn+n (15) 式中:hf是远场在角度域中的稀疏表示;hn是近场在极域中的稀疏表示。 由于hf和hn都具有稀疏性,因此可使用CS算法以较低的导频开销估计出XL-MIMO信道的状态信息。结合1.2.3节提出的XL-MIMO混合场信道模型,考虑在实际环境中信道稀疏度难以获取,本文提出一种基于SWOMP算法的混合场信道估计方案。 传统的贪婪算法采用内积准则度量测量矩阵与残差之间的相似性,然而内积准则的实质是通过测量矩阵和残差之间的角度余弦值大小来判断相似性,考虑到在原子预选时采用的内积准则不能有效地保留每个向量的特征信息,容易导致迭代过程中原子信息的丢失,为了提高原子选择的准确性,借鉴文献[13]中的算法,利用Dice系数准者选择从测量矩阵中选择与残差最匹配的原子。 具体来说,本节根据不同场信道的稀疏性,估计出不同的路径分量,最后得到混合场信道。混合场信道估计算法(HF-SWOMP)流程总结如下: 输入:y,P,F,W,S,α 输出:h 初始化:r=y,Ωf=∅,Ωn=∅ 步骤1计算远场传感矩阵:Af=PF。 步骤3令Ωf=Ωf∪J0,hf=0N×1。 步骤4求最小二乘解:hf(Ωf)=pinv(Af(:,Ωf))y,其中pinv()表示求伪逆。 步骤5更新残差:r=y-pinv(Af(:,Ωf))y。 步骤6t=t+1,如果t≤S则返回步骤2中继续迭代;如果t>S或则残差r=0则停止迭代,同时保留最后一次所得为hf。 步骤7计算近场传感矩阵:An=PW。 步骤9令Ωn=Ωn∪J0,hn=0N×1。 步骤10求最小二乘解:hn(Ωn)=pinv(An(:,Ωn))y,其中pinv()表示求伪逆。 步骤11更新残差:若Ωf=∅,r=y-Anhn,若Ωf≠∅,r=y-Anhn-Afhf。 步骤12t=t+1,如果t≤S则返回步骤8中继续迭代;如果t>S或则残差r=0则停止迭代,同时保留最后一次所得为hn。 步骤13令对状态矩阵初始化:h=0N×1。 步骤14若Ωf=∅,h=h+Whn;若Ωn=∅,h=h+Phf;若Ωn≠∅且Ωf≠∅,h=h+Phf+Whn。 步骤15输出混合场信道矩阵。 在HF-SWOMP算法中,S为最多迭代次数,默认设置为10次;α为阈值门限参数,Th=α×max(u)为每次迭代的阈值门限取值,其大小随着最大相关系数变化而变化;Ωf和Ωn分别为远场和近场路径分量关联的集合,初始化为空集。第一阶段(步骤1~6)远场路径算法和传统SWOMP算法相同,第二阶段(步骤7~12)相比第一阶段的区别是在步骤11更新残差时不仅要去掉部分近场路径分量的贡献,还需去掉所有远场路径分量的贡献。 为了分析所提XL-MIMO混合场信道估计算法的性能,同时对比传统算法的差异,本文采用Matlab搭建下行单用户混合场系统传输模型进行相关仿真,具体仿真配置参数如表1所示。 表1 仿真配置参数Tab.1 Simulation configuration parameters 图4对比了HF-SWOMP不同阈值门限参数α取值的归一化均方差(Normalized Mean Square Error,NMSE)性能在不同信噪比下的差异。从图中可以看出,随着信噪比的增加,不同阈值条件下的算法NMSE性能都有所提升。随着阈值门限参数α取值的增加,算法每次选择的原子数越少,选择错误原子的概率越小,其性能越好;当阈值门限参数α取值为0.9时,性能最好,因此后续仿真中算法的阈值门限参数α均为0.9。 图4 不同阈值门限参数取值的NMSE性能Fig.4 NMSE performance for different values of α 图5对比了本文所提算法与基于LS、HF-SWOMP、SWOMP、HF-OMP和HF-GOMP的信道估计算法在不同信噪比条件下的NMSE性能,其中路径参数γ=0.5,HF-GOMP每次迭代选择的原子数为3,HF-OMP为混合场信道估计算法、SWOMP分别在单一近场或远场条件下进行估计。从图中可以看出,随着信噪比的增加,几种不同的信道估计算法的NMSE性能都有所提升。本文所提的HF-SWOMP混合场算法在性能上优于采用单一远场或近场的SWOMP算法。而HF-OMP算法每次只选择一个原子,因此能更精确地选取原子,算法性能更好,但HF-OMP算法需要已知信道的稀疏度,在实际信道中难以实现。在HF-OMP算法的基础上,HF-GOMP算法每次固定选择3个原子,加快了算法的迭代效率,但也加大了引入错误原子的概率,性能有所下降。LS算法不仅性能低于本文所提算法,并且还会产生极大的导频开销。由此可见,本文所提算法在实际信道中能取得更好的效果。 图5 不同算法在不同信噪比下的NMSE性能Fig.5 NMSE performance of different algorithms at different signal-to-noise ratios 图6比较了不同算法在不同可调参数γ下的NMSE性能,其中SNR=4。从图可以看出,当γ=0时,混合场系统等同于近场模型,因此HF-SWOMP算法与基于近场模型的SWOMP算法性能相同;当γ=1时,混合场系统等同于远场模型,因此HF-SWOMP算法与基于远场模型的SWOMP算法性能相同;在γ∈(0,1)时,HF-SWOMP算法的性能均优于其他几种算法,特别是当γ=1/3时其性能达到最优。 图6 不同路径参数取值的NMSE性能Fig.6 NMSE performance for different values of path parameters 图7比较了各算法在不同信噪比条件下的单次运行时间。由于HF-OMP算法每次只选择1个原子且迭代次数等于稀疏度,因此迭代次数不变,算法运行时间较长且受信噪比增加影响较小。相较于HF-OMP,HF-GOMP算法每次固定选择3个原子,迭代次数比HF-GOMP少,算法运行时间有所减少。HF-SWOMP算法每次选择的原子数和迭代次数与信噪比有关,随着信噪比的增加,HF-SWOMP算法能更精确地选择原子,引入错误原子概率降低,算法迭代次数降低,算法运行时间减少。在相同信噪比条件下,本文所提的HF-SWOMP算法运行时间低于上述两种算法的运行时间。 图7 不同算法的运行时间Fig.7 Running time of different algorithms 本文基于XL-MIMO混合场信道的稀疏性进行建模,同时考虑到实际信道中稀疏度难以获取,提出了一种稀疏度自适应的混合场信道估计算法。主要思想是通过分析近场和远场的信道特性,建立一个混合场信道模型,然后通过改进SWOMP算法,提出了HF-SWOMP算法对混合场信道进行估计。仿真结果表明,在降低导频开销的同时,本文所提算法不需要知道信道的稀疏度,还能获得较好的NMSE性能。通过更改可变参数,调节近场和远场路径分量的比例,现有的单一信道估计方案都可以看作是混合场信道估计方案的特殊情况。 在未来XL-MIMO混合场信道的研究中,可以考虑近场和远场信道中的稀疏特性,采用更先进的CS算法来估计混合场信道中的系数分量。1.2 信道模型
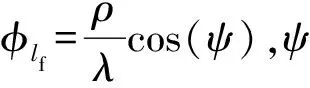
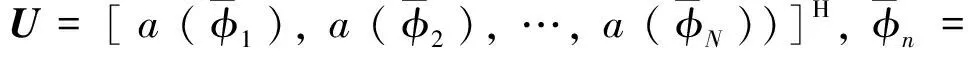

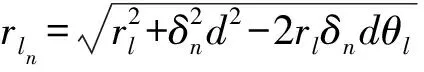
b(θN,rN1),…,b(θN,rNsN)]
2 混合场信道估计方案
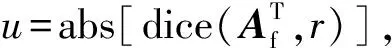

3 计算复杂度分析
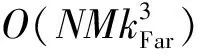
4 仿真结果与分析

5 结束语
