C/O与C/H测井响应的数值模拟对比研究
2024-04-29李巽吴文圣董夺
李巽 吴文圣 董夺
(中国石油大学(北京) 北京 102249)
为研究评价在生产上有开采价值的油藏饱和度方法,C/O测井的研究逐步展开,如今C/O测井主要应用在油藏开发中后期的套管井中,用于确定注水开发油田的剩余油饱和度[1]。我国C/O测井技术发展较晚,在经历单晶、双晶、双探测器的C/O饱和度测井仪器发展后,已经较为成熟[2]。但由于井下环境复杂,C/O在饱和度计算方面受很多因素影响。2019年,王瑞刚等[3]就砂岩C/O测井能谱处理方法开展研究,利用中子脉冲期间获得的混合光谱和中子脉冲后测量的俘获光谱进行解谱,提高了饱和度计算的精度;2022年,王振等[4]开展了砂泥岩储层的C/O测井泥质校正方法研究并加以应用,结果显示,经过泥质校正后的剩余油饱和度解释误差不超过10%;2022年,Sudac等[5]开发了配备高温α粒子探测器的碳-氧(C/O)中子测井仪器,降低了井眼环境的影响,提高了地层分辨率和探头耐高温能力。
C/O测井作为在低矿化度储层主流的饱和度测量方法得到了广泛的发展,但它在低孔隙度条件下测量精度低的问题仍然没有得到有效解决,这些年陆续有人在核测井领域开发新方法来解决这一问题[6],其中最为典型的就是C/H地层流体饱和度测井(Carbon-Hydrogen fluid saturation log),也称FCH测井方法。根据多年的研究与实践成果表明,C/H测井用于低矿化度套管井饱和度测量是完全可行的[7-8]。2014年,马建国等[9]推出了FCH地层流体饱和度测井方法,并将该技术进行了实际应用,后又对该方法加以改进,进一步提高测量结果准确性扩大应用范围[9]。C/H测井的实现可以为低孔隙度储层提供更加可靠的饱和度数据,全定量评价储层的含油饱和度及油层水淹程度,发现剩余油分布规律以及边底水动态[10]。
本文将借助MCNP,参考Halliburton公司的C/O测井仪器储层性能检测仪(Reservoir Performance Monitor,RPM)建立数值模拟模型,研究C/H测井相较于C/O测井方法在不同井眼和地层环境下对含油饱和度计算的优势与劣势。
1 理论基础
利用脉冲中子源向地层发射14.1 MeV的高能中子,中子与地层原子首先发生非弹性散射释放非弹γ射线,再发生弹性散射,当中子被减速为慢中子时又与地层原子发生辐射俘获反应,产生俘获γ射线,从而获得地层的非弹γ能谱和俘获γ能谱,通过分析这些能谱可以确定地层元素含量和含油饱和度[11-14]。
非弹性散射截面与目标原子序数是密切相关的,一般来讲,原子序数越大,发生非弹性散射的截面越大。在地层中C元素和O元素虽然原子序数并不高,但含量很高,它们与快中子非弹性散射产生的γ射线是探测器γ计数的主要来源。同时由于C和O元素产生γ射线的能量高,可以很容易在能谱中识别出他们的特征峰。
H元素虽然很难与快中子发生非弹性散射,但发生俘获反应的截面却很高,可以通过中子与原子核发生俘获反应释放的俘获γ射线识别H元素。
采取能窗法获得能谱特征峰区域的计数,将C峰计数与O峰计数做比得到C/O测井响应;将C峰计数和H峰计数做比得到C/H测井响应。由体积模型法计算得到C/O和C/H与孔隙度和饱和度之间关系,如下:
式中:RCO为C/O值;nC和nO分别为单位体积地层中C原子和O原子的摩尔数;φ为地层孔隙度;So为含油饱和度;K1、K2、K3、K4和K5为常数,由地层矿物组成和流体密度等因素决定。由式(1)可知,孔隙度一定时,含油饱和度越大,RCO越大;在地层含油饱和度一定时,孔隙度越大,RCO越大。
式中:RCH为C/H值;nC和nH单位体积地层中C和H元素原子的摩尔数;L1、L2、L3、L4和L5为常数,由地层矿物组成和流体密度等因素决定,可以很容易得到L5>L1>L4。由式(2)可知,在孔隙度一定时,含油饱和度越大,RCH越大;在含油饱和度一定时,孔隙度越大,RCH越小。
2 计算模型
本文利用MCNP5,使用的截面数据库为ENDF/B-VII,设计的计算模型如图1所示。考虑到在套管井中C/O测井是仪器居中测量的[15-16],因此建立RPM仪器模型(即仪器结构采用Halliburton公司的C/O测井仪器RPM)如图1(a)所示。同时,为了便于对比,设置无井眼环境影响的球状模型如图1(b)所示。
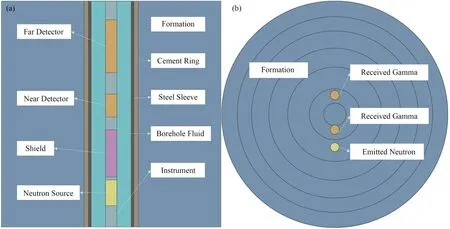
图1 MCNP 计算模型示意图 (a) RPM仪器模型,(b) 球状模型Fig.1 Diagram of the MCNP model (a) RPM instrument model, (b) Spherical model
图1(a)为RPM仪器模型在X、Z方向上的投影,由外到内依次是地层、水泥环、钢套管、井内流体和仪器,仪器由下至上分别是脉冲中子源、屏蔽体、短源距γ探测器和长源距γ探测器,源距分别为33.02 cm和58.42 cm。图1(b)为球状模型在X、Z方向上的投影,建模物质仅为地层的矿物和流体,没有井眼和仪器的影响,仅在相应栅元设置发射中子或接收γ的功能。如表1和表2所示,分别是两种数值模拟模型共同的地层物质组成,和RPM仪器模型特有的井眼及仪器的信息。

表1 地层物质组成Table 1 Formation material composition
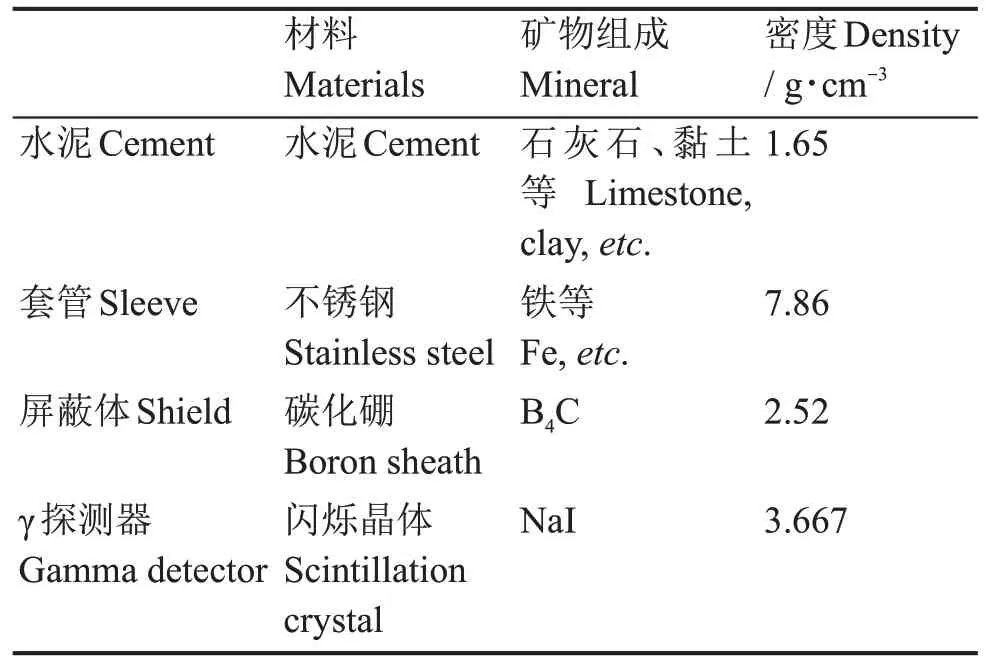
表2 井眼及仪器信息Table 2 Well and instrument information
在设计中子脉冲序列时(图2),以100 ms为一个发射周期,前40 ms发射14 MeV的单能快中子,后60 ms不发射中子。由于非弹性散射发生时间非常快,几乎是与中子发射同时产生同时结束,因此在0~40 ms设置第一个窗口用于接收非弹γ射线,在45~100 ms设置第二个窗口用于记录俘获γ射线。
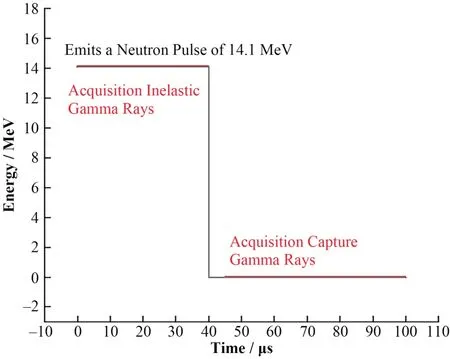
图2 中子脉冲序列Fig.2 Neutron-emission pulse sequence
采用能窗法获取C和O两种元素对应特征峰区域的非弹γ计数率和H元素对应特征峰区域的俘获γ计数率,能窗选择为:H窗2.16~2.30 MeV,C窗4.40~4.45 MeV,O窗6.050~6.225 MeV。
3 测井响应对比分析
基于上述能窗选择和脉冲中子序列,分别使用球状模型和RPM仪器模型进行MCNP数值模拟,得到C、O和H元素的能窗计数,利用能窗计数得到不同岩性、孔隙度和饱和度条件下C/O和C/H与地层饱和度和孔隙度的响应关系,以及他们对饱和度的灵敏度。油水灵敏度计算公式如下:
式中:Dsen为C/O或C/H对饱和度的灵敏度;Yo为储层纯含油时C/O或C/H的值;Yw为储层纯含水时C/O或C/H的值。
3.1 球状模型
忽略井眼影响,采用球状模型进行数值模拟得到不同岩性地层下C和O两种元素对应能窗的非弹γ计数率,改变截断时间和能窗范围得到H元素对应能窗的俘获γ计数率,各元素对应能窗计数做比得到C/O和C/H的值,绘制不同孔隙度和饱和度条件下C/O和C/H值与饱和度和孔隙度的关系曲线,以及它们对饱和度的灵敏度曲线,如图3和图4所示。

图3 球状模型下不同地层中碳氧比与孔隙度和含油饱和度的关系及对饱和度灵敏度Fig.3 Relationship between C/O ratio and porosity, saturation, along with its sensitivity to saturation in different strata under the spherical model

图4 球状模型下不同地层中碳氢比与孔隙度和含油饱和度的关系及对饱和度灵敏度Fig.4 Relationship between C/H ratio and porosity, saturation, along with its sensitivity to saturation in different strata under the spherical model
从图3和图4可以看出,在砂岩和石灰岩地层中忽略井眼环境的影响,C/O和C/H关于孔隙度的走势是相反的。C/O随孔隙度增大,随饱和度增大,且C/O对饱和度的灵敏度也随孔隙度而增大;C/H随孔隙度增大而减小,随饱和度增大,且C/H对饱和度的灵敏度也随孔隙度增大。
同时,在图3和图4中还可以看出,在砂岩地层中没有井眼环境的影响下,C/H对饱和度的灵敏度要整体好于C/O,也就是说在砂岩地层中低孔隙的状况下C/H对饱和度的灵敏度也高于C/O的灵敏度。这表明C/H可以在低孔隙度条件下更好反映地层含油饱和度状况。然而,一个更明显的趋势是C/O和C/H对砂岩的灵敏度都要高于石灰岩,尤其是C/H对两种岩性的灵敏度差异几乎是两个数量级,这表明骨架中的C元素会影响C/O和C/H的响应灵敏度,而C/H对饱和度的响应关系并没有C/O稳定。
3.2 RPM仪器模型
将球状模型替换为简化过的RPM仪器模型,此时得到的石灰岩和砂岩地层中的数据都考虑了井眼和环境的影响,更加贴近生产实际。绘制的不同孔隙度和饱和度条件下的C/O和C/H与饱和度和孔隙度的关系曲线,以及它们对饱和度的灵敏度曲线,如图5和图6所示。
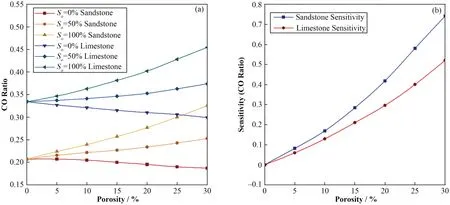
图5 RPM仪器模型下不同地层中碳氧比与孔隙度和含油饱和度的关系及对饱和度灵敏度Fig.5 Relationship between C/O ratio and porosity, saturation, along with its sensitivity to saturation in different strata under the RPM instrument model
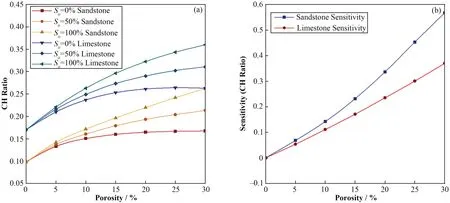
图6 RPM仪器模型下不同地层中碳氢比与孔隙度和含油饱和度的关系及对饱和度灵敏度Fig.6 Relationship between C/H ratio and porosity, saturation, along with its sensitivity to saturation in different strata under theRPM instrument model
从图5和图6可以看出,在砂岩和石灰岩地层中考虑井眼环境的影响,C/O和C/H的测井响应都随孔隙度而增大,随饱和度而增大,且他们对饱和度的灵敏度也随孔隙度而增大。对比C/H与C/O测井响应对饱和度的灵敏度发现,C/H对饱和度的灵敏度略低于C/O的灵敏度,这说明C/H与C/O同样适合两种岩性套管井的饱和度估计,但C/H无法解决C/O在低孔隙度条件下饱和度估算准确度低的问题。
然而,从图4和图6中可以发现,在是否消除井眼影响的两组模型中C/H对孔隙度的响应效果是完全相反的。在忽略井眼影响的球状模型中(图4),C/H随孔隙度的增大而减小;在考虑井眼影响的RPM仪器模型中(图6)C/H随孔隙度而增大。这里考虑本底C能窗计数率和H能窗计数率的影响。利用体积模型法计算C/H与孔隙度的理论关系如式(2)所示。式中:C元素来自于孔隙流体和骨架,H元素来自于孔隙流体。在这里由于不考虑饱和度的影响,对式(2)进行简化如下:
式中:A、B和C为与孔隙度无关的常数。
然而,在进行蒙特卡罗数值模拟时,由于能谱法本身的不准确性,C元素和H元素能窗内的计数率可能还由Si和O元素贡献,且在RPM仪器模型中由于井内流体是水,模拟得到的H元素的计数率要远大于实际H元素的计数率。这里把由于以上两种情况而产生的C和H元素的计数称为本底计数。在公式中加入本底的C计数nCbg和H计数nHbg得到如下:
对式(5)求导:
在球状模型下,可以近似使nCbg=nHbg;根据体积模型法很容易可以计算出,无论在砂岩还是石灰岩中C>A恒成立,从而得到(RCH)′<0,这就对应了球状模型下C/H随着孔隙度的增大而减小。
在RPM模型下,由于井内流体为水,因此本底H元素的计数会很大,可以近似使nHbg≫nCbg,从而得到(RCH)′>0,这就对应了RPM模型下C/H随着孔隙度而增大。
因此,在是否考虑井眼影响的不同模型中进行数值模拟得到C/H与孔隙度关系完全相反并不是因为数值模拟出现错误,而是受井眼环境影响所致的必然结果。在实际应用中,考虑井眼环境影响的RPM模型更有现实意义。换一种角度,井眼条件改变了C/H与孔隙度的关系却没有改变它与饱和度的关系,进一步说明C/H与饱和度关系比它与孔隙度的关系更稳定。
4 结语
1) 在忽略井眼环境影响且孔隙度较高时,C/H和C/O对地层流体饱和度都具有较高的灵敏度,可用于估算地层饱和度。在砂岩地层中C/H的灵敏度要高于C/O,理论上可以用来解决C/O在低孔隙度条件下饱和度估算灵敏度低的问题。
2) 在考虑井眼环境影响时,C/O对饱和度的灵敏度更大,更适合用于套管井饱和度估计。
3) C/H测井响应与C/O相比,受井眼环境影响更大,对饱和度的灵敏度不稳定,不适合在复杂井眼环境中应用;C/H和C/O都受骨架中C元素含量影响,当骨架C含量过高时,地层流体饱和度估算结果精度将变低。
作者贡献声明李巽负责数值模拟及论文编写修改工作;吴文圣负责文章思路的提出指导及框架的把控;董夺负责数值模拟方案的指导。
