基于机器人与机床联合工作的误差测量与解耦*

苗奎奎,李 巍,闫利文

(1.天津理工大学a.天津市先进机电系统设计与智能控制重点实验室;b.机电工程国家级实验教学示范中心,天津 300384;2.天津中德应用技术大学机械工程学院,天津 300350)

0 引言

随着工业智能化不断提升,机器人技术在制造业中的用途愈发广泛,各种机器人的设计制造也朝着分工更加细化的方向发展。在机器人进行实际工作过程中,由于振动、重力、控制等多种原因,机器人的执行末端会产生多种误差[1]。中外许多学者针对于此开展了理论及应用研究,唐越等[2]使用激光跟踪仪作为测量系统对机器人末端定位误差参数进行辨识研究,廖昭洋等[3]学者使用时空混合图卷积网络对机器人的定位误差进行了预测以及补偿,高贯斌等[4]利用卡尔曼滤波算法对机器人运动学参数误差进行辨识,并提出一种关节空间插值误差补偿法对误差进行补偿。MACFARLANE等[5]提出基于DAT的方法,对机器人轨迹进行误差辨识与补偿的一体完成,但由于其计算复杂性,不利于应用。潘海鸿等[6]通过建立位置误差模型,并采用最小二乘法来识别机器人关节原点误差。

数控机床作为一种传统加工制造业工作母机,其误差辨识技术较为成熟,项四通等综述了数控机床几何误差方面的研究新进展,并且系统地分析了机床误差测量与建模需解决的技术难点[7],WANG等[8]以四元数为理论支持,提出了一种针对任意旋转轴位置的五轴几何误差的通用识别模型,根据该模型中的轨迹平衡算法,可以解决DBB轨迹运行中运动与数据采样的异步问题。李晓晓等[9]利用“十二线法”进行机床几何误差元素辨识研究。OSEI等[10]使用齐次变换运动矩阵推导出误差模型,该模型可以提高工作台倾斜时PIGEs误差的识别效率。李国龙等[11]采用球杆仪来快速测量辨识数控机床转台位置相关几何误差。

无论是数控机床还是定位机器人作为智能化物流中重要一环,在柔性化生产线中进行制造配合的趋势越发紧密,将工作站与机器人联合工作也成为当今许多柔性化智能化生产线的选择。在上述发表的研究成果中,均将机器人、数控机床作为一种单一工作站进行研究,并不能完全满足智能化联合作业的生产现状。本文基于多体动力学理论,从总体角度将两个工作主体联系起来进行综合误差分析。

1 综合误差模型与测量方法

1.1 综合误差模型

如前述,若将机器人与数控机床进行的工作视为相互独立,则二者可分别进行独立研究,其进行联合工作时的误差将变得不可量。本文为了开展二者的工作相对误差研究,将机器人与数控机床作为一个整体进行分析。其机械结构包括2个直线轴X和Y以及8个旋转轴B、C、R1～R6。其中B轴作为机床的摆动轴,围绕X轴旋转;C轴为机床回转工作台,绕Z轴旋转;R1～R6为机器人的6个旋转轴,如图1所示。

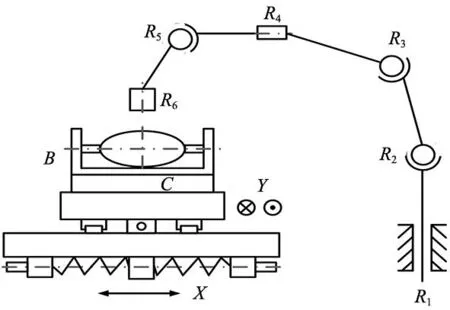
图1 机器人与五轴机床工作台运动支链

应用多体动力学中的微小位移原理,对6自由度(6R)串联工业机器人及双转台结构五轴数控机床工作台进行拓扑分析,如图2所示。其中,MCS为机床坐标系(机器人世界坐标系),与地面固定。TCS和WCS分别是机器人工具坐标系和机床工件坐标系,机床测头固定在TCS上,它们分别代表机器人和机床运动的两个末端。XCS和YCS表示机床的进给轴坐标系,而BCS和CCS则代表机床的两个旋转坐标系,R1CS～R6CS为机器人的6个旋转坐标系。图中机床测头标记为IP,其工作在机床工件坐标系与机器人工具坐标系之间,反映由MCS→XCS→YCS→BCS→CCS→WCS以及MCS→R1CS→R2CS→R3CS→R4CS→R5CS→R6CS→TCS两条运动支链之间的综合误差。

图2 机器人与机床联合误差辨识拓扑图

1.2 误差测量方法

当数控机床与机器人协同工作时,两个运动支链都会产生显著的位置误差。此外,这两个运动支链在不同的运动轨迹和位姿下误差值不同。在其工作空间中为了便于研究机床与机器人位置误差的特性,将联合工作时产生的误差归结为机床运动支链所产生的误差,从而方便后续建立误差测量模型和误差解耦。

基于上述的研究思路,将机床测头安装在机器人末端法兰上,机床测头信号接收装置与数控机床连接,如图3所示。首先,进行测量前标定,将测量所使用的工件装夹在机床上,移动机器人使测头与工件接触,将该点设定为测头测量的基坐标,并且记录机器人示教器上机器人当前的位置信息;其次,在机床辨识轨迹上选取一系列的点,并将机器人移动到相应点的位置,机床重复运动轨迹使得工件与测头进行直接接触测量;最后,为了得到实际位置坐标值将测头测量的位置坐标转换到机器人基坐标系,并将实际坐标值与机器人示教器中读取的理论坐标值进行比较,可得机器人与数控机床联合工作时的误差。

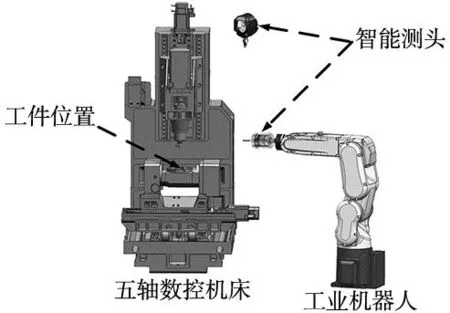
图3 机床与机器人位置关系

2 误差辨识轨迹与误差建模

2.1 轨迹生成

使用样条曲线作为数控机床的辨识轨迹,设具有n+1个控制顶点Pi的k次样条曲线表达式为:

(1)

当其节点矢量U[u0,u1,…,ui+2k+1]不为常数时,则产生NURBS曲线,式(1)中Pi为控制顶点,Bi,k为调和函数,其标准形式为:

(2)

式中:Wi为控制顶点的全因子。

NURBS曲线在每个辨识点Pi产生的误差矢量ΔP会导致理论轨迹的偏移及旋转。将产生的实际位置表示为Pio,如图4所示为在机器人基坐标系产生的空间曲线。理论与实际轨迹端点坐标分别为Pp(xp,yp,zp)、Pq(xq,yq,zq),其径矢为rp(rpx,rpy,rpz)T及rq(rqx,rqy,rqz)T,基矢量为(e1,e2,e3),式(3)中ΔP为其在空间中的误差矢量,用两轴之间的夹角α、β来表示ΔP在空间中的角度,其方向余弦如式(4)所示。

(3)

图4 NURBS辨识轨迹误差

(4)

2.2 误差建模

在数控机床两个移动轴以及两个旋转轴上建立相应空间坐标系,空间坐标系中6个空间自由度对应6项误差元素,并且两个移动轴之间互相存在垂直度误差和平行度误差,总计27项误差元素。

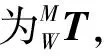
(5)

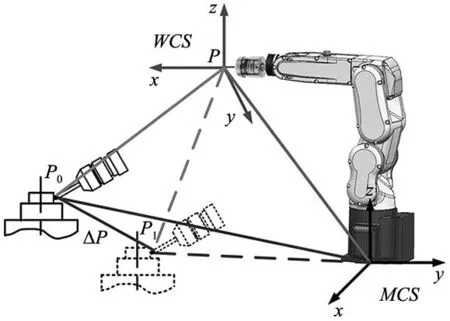
图5 误差测量原理

式中:Px、Py、Pz分别为测头坐标系原点P在机器人基坐标中的位置坐标值。设机床测头坐标系下测量得到的实际位置坐标为P0,机器人基坐标系下的任意一个轨迹点的理论位置坐标值为P1,则可计算得机器人基坐标系下的位置误差值ΔP,如式(6)所示。

(6)

式中:δx、δy、δz分别为机器人基坐标系X、Y、Z方向上的位置误差值。则可以用理论位置点与实际位置点之间的距离ΔR表示机床与机器人联合工作产生的位置误差,表达式如式(7)所示。

(7)

(8)

在考虑误差影响情况下的实际坐标Rq:

(9)

式(8)中各项具体参数由式(10)～式(12)给出。其中涉及到的各误差元素的定义如表1所示。

(10)

表1 误差缩写和计量单位

(11)

(12)

3 实验验证

3.1 实验准备

实验设备如图6所示,左侧为双转台式五轴数控加工中心,其控制系统为Sinumerik 840Dsl,具备五轴数控系统插补功能。右侧为工业机器人FANUC LR Mate 200iD7L。使用雷尼绍机床测头作为测量工具,测头安装在机器人末端的法兰上,其信号接收装置与机床数控系统相连,测头的绝对测量精度为±1.5 μm。实验在温度范围为(20±2) ℃,温度为50%±5%的恒温恒湿环境下进行。为了消除测头安装过程所产生的误差,在测头安装好后进行测头坐标系的标定,保证在实验过程中测头坐标系与机器人基坐标系相对位置保持固定不变。实验过程中为了避免机床热误差对误差值的耦合影响,在机床热机6 h后依据生成的空间样条曲线进行误差辨识实验。

图6 实验装置图

3.2 误差测量及解耦数据分析

如2.1节所述,机床运行轨迹选用NUBRS曲线。参见图7将轨迹分成4个辨识区,每个辨识区选取25个主要辨识点,共计选取100个辨识点。在进行实验时,由于有27项误差元素待辨识,每个辨识点需进行27次实验进行数据收集。

图7 辨识区间

根据空间向量的角度计算公式,以上述曲线作为研究对象,对辨识曲线各点进行理论矢量角度分解,与式(10)相关的各矢量角度参数α、β由式(4)计算得出。

将NURBS曲线各点的坐标参数、机器人示教器中读取的理论坐标参数以及机床测头测出的实际坐标参数代入式(8)中,对该矩阵进行满秩验证后,将此解耦问题转化为多元非线性方程组的求解问题,并使用最小二乘法对27项误差元素进行解耦,结果如图8所示。

(a) εxx、εxy、εxz解耦结果 (b) δxx、δxy、δxz解耦结果

对比分析图8中的数据,可以得出:

(1)在同一轨迹的不同辨识区中所形成的误差不同。

(2)在同一误差辨识区中,各个误差元素呈现出连续变化的形式。

(3)误差的变化趋势基本上符合曲率越大,误差越大的规律。

(4)旋转误差产生的大小与轨迹旋转方向基本上无关,旋转误差的值不受轨迹旋转转向的影响。

4 结论

通过误差建模与实验,本文提出了一种基于机床测头测量机器人与数控机床联合工作误差的方法。该方法采用收集机床运动时不同轨迹点的方式,快速测量并计算出机器人与机床联合工作时产生的空间误差。将测得的空间误差归结到数控机床运动支链,通过解耦可以有效地辨识出机床4个坐标系下的全部27项误差元素。以机床作为实验的主要研究对象,验证了数控机床在不同运动轨迹所产生的误差并非常量,并且揭示了各误差元素差生的误差值与不同运动轨迹之间的规律。实验结果表明,该方法的精度等级可满足机床加工及补偿需求。以该测量及解耦方法为基础,为后续误差运动解耦分析、误差补偿、数控机床插补轨迹优化及机器人运动支链的误差解耦研究奠定基础。