基于有限元模型的沥青混凝土心墙坝动力反应分析

卢建南，成 斌

(新疆水利水电勘测设计研究院有限责任公司，新疆 乌鲁木齐 830000)

近年来，随着城市化进程的不断加快，我国大型水利工程的建设规模也在快速发展[1]。其中，沥青混凝土心墙坝作为一种常见的坝型，以其结构简单、施工方便以及良好的防渗和抗震性能而被广泛应用于水利工程之中[2-3]。然而，随着设计要求的不断提高和安全性能的逐渐加强，对于沥青混凝土心墙坝的动力反应研究也变得尤为重要。

沥青混凝土心墙坝在一些高地震区的广泛应用，对于水利工程的安全稳定性有着重要的影响[4-5]。传统的静态分析方法很难充分考虑到水利工程在动荷载下的实际工作状态，而沥青混凝土心墙坝作为一种复杂的结构体系，其动力特性对于工程的安全性评估至关重要。因此，通过对沥青混凝土心墙坝动力反应进行深入研究，可以为实际工程提供科学依据和技术支持，提升水利工程的稳定性和安全性。

目前，关于沥青混凝土心墙坝动力反应的研究已经取得了一些进展，但仍存在一定的局限性[6]。现有研究大多侧重于传统的二维平面模型或简化的假设条件下的分析，无法充分考虑到实际工程中存在的三维复杂性问题。由于沥青混凝土材料的特殊性，现有研究成果往往无法全面揭示其在极端动力荷载下的动态响应[7]。因此，开展基于三维有限元模型的动力反应分析，深入研究其动力响应对于确保坝体的安全性和稳定性至关重要。

本文旨在基于三维有限元模型，对新疆某沥青混凝土心墙坝的动力反应进行深入研究。通过分析沥青混凝土心墙坝在地震极端动力荷载作用下的动力响应，可以为沥青混凝土心墙坝的设计、施工和运行提供科学依据和技术支持，从而更好地确保工程的安全性和可靠性。

1 计算模型及参数

1.1 动力本构模型

通过使用等效线性粘-弹性模型，可以计算出坝体材料的动力学响应。这种材料的最大动态剪切模量可以通过以下方式来描述：

(1)

(2)

将G/Gmax及阻尼比λ与动剪应变γ的动力试验数据进行回归分析，可得到动剪模量G/Gmax与动剪应变γ、阻尼比λ与动剪应变γ的关系曲线。

接触面单元的动力模型中，接触面的最大动剪模量为：

(3)

式中，σn—接触面单元的法向应力；C—接触面动力剪切试验测得的系数，C采用22.0。

接触面单元的剪切劲度K与动剪应变γ的关系为：

(4)

式中，τf—破坏剪应力，τf=σntanδ；δ—接触面的摩擦角，参数M=2.0。

接触面单元的阻尼比λ为：

λ=(1-K/Kmax)λmax

(5)

式中，λmax—最大阻尼比，计算中取为0.2。

1.2 计算模型

计算模型采用的沥青混凝土心墙坝坝高61.5m，坝长为431.42m。坝体的上游坝坡为1∶2.5，下游坝坡为1∶2.0。为了应对河谷地形的复杂性、大坝材料的多样性，以及分层填筑带来的影响，本次采用了兼具高效、跨尺度与精细特点的有限元网格划分技术，以全面模拟大坝的应力和变形。此外，还将两岸的地质特征和大坝与地基岩体的相互影响纳入考量，对两岸山体和地基岩体进行了详尽的网格划分。这些措施有力地提高了大坝动态响应计算的准确性。三维有限元模型单元数为389866个，节点数为427988个。坝体三维网格图如图1所示。

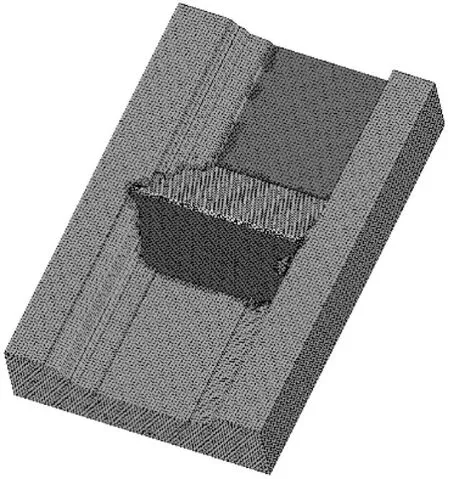
图1 坝体三维网格图

1.3 计算参数

地震永久变形分析采用Serff和Seed等提出的应变势概念为基础建立的整体变形计算方法。砂砾料、过渡料、坝基料和沥青混凝土动剪切模量系数和指数见表1。

表1 动剪切模量系数和指数

1.4 地震输入

为研究沥青混凝土心墙坝的地震动力反应，地震动输入采用坝址场地谱人工波，顺河向、竖向和坝轴向的地震加速度时程曲线如图2—4所示。该工程等级为Ⅲ等，规模为中型，工程地震设防烈度为Ⅷ度。坝址区地表50年超越概率10%的峰值加速度值为0.285g，竖向峰值加速度为水平向的2/3。

图2 顺河向地震加速度时程

图3 竖向地震加速度时程

图4 坝轴向地震加速度时程

2 地震响应计算结果分析

采用了4.0℃和9.1℃时沥青混凝土心墙动力参数进行了大坝三维动力分析，二者分布规律和最大值基本没有差别，主要以4℃时的计算结果分析大坝应力和变形的分布规律。

2.1 坝体和坝基地震反应

通过对坝体动位移分析：发现在场地谱人工波作用下，坝体的动位移会有所不同。坝体顺河向动力反应的最大动位移为0.17m，竖向最大动位移为0.05m，最大值均出现在坝顶附近，符合有限元动力计算的一般规律。大坝0+242断面最大动位移如图5所示。

图5 大坝0+242断面最大动位移(单位：m)

通过坝体加速度分析，发现沥青混凝土心墙坝的动力反应加速度都集中在坝顶附近，并且具有明显的“鞭梢效应”[8]。其中坝体最大顺河向加速度为9.0m/s2，最大竖向加速度为4.3m/s2，符合土石坝动力反应加速度的一般规律。大坝0+242断面最大加速度如图6所示。

图6 大坝0+242断面最大加速度(单位：m/s2)

2.2 心墙地震应力

在地震作用下，沥青混凝土心墙会产生压应力和拉应力。心墙静动叠加应力如图7—8所示，从图中可以看出：沥青混凝土心墙静动叠加最大压应力为4.2MPa，产生较小的拉应力，最大拉应力为0.44MPa。各心墙单元在整个地震时程中应力水平最大值如图9所示，从图中可以看出：在地震过程中，心墙最大应力水平不超过0.9MPa，主要集中在心墙底部局部范围内。

图7 心墙静动叠加最大压应力(单位：MPa，压为正)

图8 心墙静动叠加最大拉应力(单位：MPa，压为正)

图9 心墙单元在地震过程中应力水平

分别采用4℃和9.1℃情况下动力参数计算得到的心墙应力规律基本一致，不同温度参数对沥青心墙应力影响的最大值见表2。与4℃时计算参数相比，采用9.1℃参数时，心墙最大压应力与最大拉应力均略有减小。

表2 不同温度参数对沥青心墙应力影响

2.3 坝体和坝基永久变形

通过三维永久变形计算，可以更准确地预测沥青混凝土心墙坝的应力变化情况。永久变形有限元网格设置与动力有限元相同。计算得到的大坝典型断面位移如图10—11所示。大坝顺河向最大永久位移向上游为0.15m和向下游为0.55m；坝顶最大沉降为0.7m，约占坝体和坝基高度的0.44%。超高控制应综合考虑竣工后长期变形与地震永久变形影响，根据同类工程类比，采用砂砾石填筑的大坝因蠕变引起的长期沉降变形量值均在厘米级。这是由于砂砾料具有较高的压缩模量，使得其长期沉降变形量值一般不大。按照《碾压式土石坝设计规范》要求，综合数值分析和同类工程建议该水库坝顶预留竣工后沉降超高控制在1.0m左右。砂砾石坝长期变形监测结果见表3。

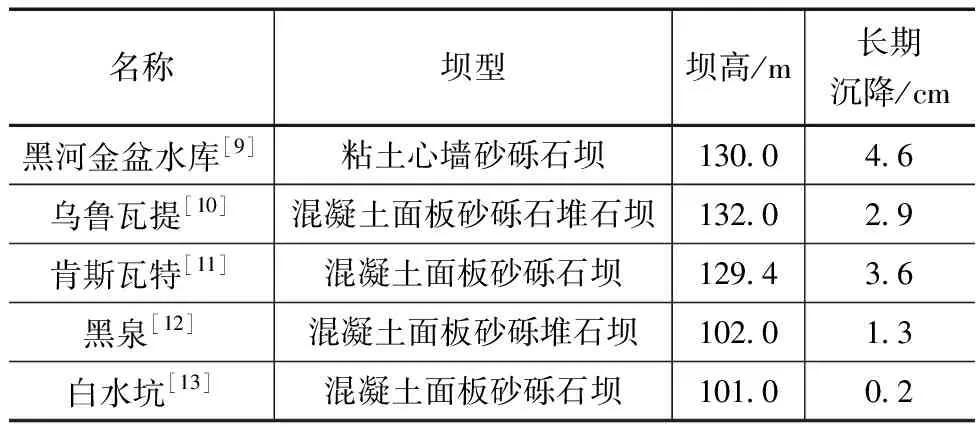
表3 砂砾石坝长期变形监测结果

图10 大坝0+242断面震后变形图(放大10倍)

图11 大坝0+242断面顺河向永久变形(单位：m，向下游为正)

2.4 心墙应力

分别采用4℃和9.1℃情况下永久变形参数计算得到的心墙位移与应力规律基本一致，不同温度参数对沥青心墙应力及位移影响的最大值见表4。与4℃时计算参数相比，采用9.1℃参数时，心墙最大压应力略有减小，但变化的幅度较小。震后心墙大主应力和小主应力如图12—13所示。

表4 不同温度参数对沥青心墙应力及位移影响

图12 震后心墙大主应力(单位：MPa，压为正)

图13 震后心墙小主应力(单位：MPa，压为正)

2.5 心墙位移

震后心墙竖向位移和轴向位移如图14—15所示。心墙竖向永久变形最大值为0.63m，主要分布在河床段心墙顶部位置，其位移分布呈现出，从河床向两岸、从心墙顶部向心墙底部逐渐减小的趋势。心墙沿坝轴向永久变形最大值为0.16m，主要分布在左岸坝段心墙顶部位置，其位移分布呈现出，从心墙顶部向心墙底部、从右岸坝段向左岸坝段逐渐减小的趋势。与4℃时计算参数相比，采用9.1℃参数时，心墙竖向位移和沿坝轴向位移略有增加，但变化的幅度较小

图14 震后心墙竖向位移(单位：m，沉降为负)

图15 震后心墙坝轴向位移(单位：m，向左岸为正)

3 结语

本文基于有限元模型对新疆某沥青混凝土心墙坝进行动力反应分析，验证了沥青混凝土心墙坝在地震作用下坝体动力响应的一般规律，主要得出以下结论：在地震作用下，坝体顺河向最大永久位移为0.55m，坝顶最大沉降为0.70m，约占坝体和坝基总高度的0.44%。心墙静动叠加最大压应力为4.2MPa，最大值拉应力为0.44MPa。心墙竖向位移最大值为0.63m，主要分布在河床段心墙顶部位置。沿坝轴向位移最大值为0.16m，主要分布在左岸坝段心墙顶部位置。沥青混凝土心墙坝在遭遇设计地震后坝体的动力反应结果符合类似工程经验，沥青混凝土心墙拉应力和压应力均较小，应力水平在合理范围内。

综上所述，当沥青混凝土心墙坝在Ⅷ度地震作用下，坝体仍具有较好的抗震安全性能，计算结果可以为类似工程提供参考。