丁坝结构对水流流态及床面变形的影响研究

吴建军

(新疆塔里木河流域和田管理局，新疆 和田 848000)

0 引言

丁坝结构研究是流域治理的重要研究课题。从水力学角度看，丁坝是为了保持河道稳定而修建的，用于通航、灌溉、供水和保护河岸免受冲蚀磨损[1]。由于丁坝周围的多样化流动创造了适合河岸植被和水生生物群落的条件，因此，丁坝也被修建在河道中，用于生态系统的保护。

根据结构的渗透性可将丁坝分为两类：不透水丁坝和透水丁坝[2]。第一类一般使用当地的岩石、碎石或石笼建造，第二类由一排排桩、竹子或木材组成。2类丁坝以不同的方式影响流场和泥沙输移，导致不同的流态和床面形态。然而，丁坝对周围水力形态的影响尚不完全清楚[3]。在很多情况下，主航道的深化是一个可取的结果，而丁坝趾附近的局部冲刷和主航道的泥沙沉积对丁坝结构的稳定性和可用性是不需要的[4]。为了更好地理解丁坝区域的流动和床面变形，许多研究都是在单个丁坝的情况下进行的[5]。但在实际应用中，由于丁坝通常被组织在一个群体中，因此仍需要进行大量的研究。

本研究拟对2个不透水或透水丁坝周围的水流和局部冲刷进行研究。采用室内试验和数值模拟相结合的方法。实验能够在特定和受控的条件下提供可靠的信息。流动分离和涡的形成等过程的相似性将为验证建模工具提供更通用的应用。鉴于此，开发了基于非结构化网格的三维数值模型。将模拟结果与实验结果进行了对比。

1 材料与方法

1.1 室内实验

室内试验所用水槽长10m，宽0.80m，深0.28m。对于所有实验，通道的床面坡度调整为1/800。实验装置的详细示意图如图1所示。

图1 实验装置示意图(单位：cm)

x轴从动床始端开始，y轴从水槽右壁开始，z轴从初始平床面开始。上游入口处有一张固定床，由木板制成，高出床底10cm。木板的作用是平滑水流。在试验小区的水槽左侧垂直于槽岸布置2个丁坝。在案例1中，使用了由木质长方体制成的不透水的丁坝。案例2中，透水丁坝为一系列圆棒，设计透水率为50%。所用沉积物为煤，平均粒径为0.83mm，比重为1.41。

试验在均匀流条件下进行。实验所采用的水力参数见表1。

表1 实验条件说明

通过调节量水槽的尾门高度，建立均匀流条件。恒定的泥沙速率从水槽上游边界源源不断地供给，以维持动态平衡状态。干泥沙在补给前与水混合，以避免弥散效应。输沙率采用推移质输沙率公式进行计算，但输沙量最终通过一些试验进行调整。每次实验持续5h足以达到动态平衡条件。

在下游边界处，采用尾门控制水位。水槽完全排水后，用点式水位计测量水位，通过激光传感器获得床面变形。对于速度场的测量，采用胶结物来固定最终的床层变形。固定好床后，使用两个电磁测速仪来测量施加相同流量丁坝周围的流速。考虑到床面粗糙度的影响，水泥和沉积物(煤)之间没有差异，这可能会导致速度结果的变化。

1.2 数值模型

暂时采用数值模型对基于固定床条件下的流场进行模拟。所提出的数值模型的控制方程基于定常的3D RANS(雷诺平均Navier-Stokes方程)和连续性方程，可在笛卡尔坐标系下用张量表示如下：

(1)

(2)

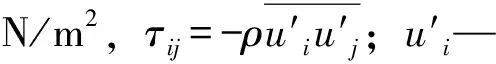
湍流闭合采用标准k-ε模型。雷诺张量通过线性本构方程获得：

(3)

(4)

式中，k—湍流动能，m2/s2；δij—克罗内克符号δ；vt—涡黏性，N/m2；Sij—应变率张量，N/m2；Cμ—系数，设为常数=0.09；ε—湍流动能的耗散率，W/m3。分别用以下2种输运方程来估计k和ε：

(5)

(6)

式中，G—湍流动能k的产生速率，定义为：

(7)

在模拟中，入口边界为狄利克雷边界，所有的量都是规定的。出口边界设置在远离丁坝的区域，假设为一个具有零梯度的Neumann边界。在不透水边界附近采用壁面函数法。在模拟中，可渗透的丁坝被表示为一簇不透水的丁坝，每个可渗透的丁坝用一些细密的网格表示。

模拟序列采用SIMPLE(压力联立方程的半隐式方法)程序。首先，对每个速度分量求解动量方程，其中压力、涡黏性、湍动能及其耗散率是已知的。合成的速度场被用来计算通过控制体积面的质量通量。压力修正方程求解后，速度场得到改善。最后，求解湍流动能及其耗散率的输运方程并更新涡黏性。重复上述过程，直到残差水平足够小或覆盖规定的最大迭代步数。

2 结果与讨论

2.1 实验结果

平衡条件下的床层变化如图2所示。

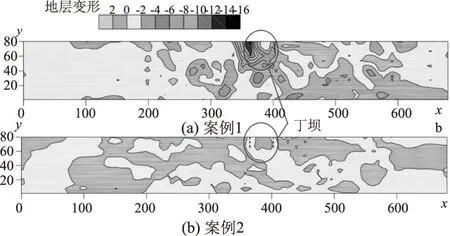
图2 平衡条件下案例1和案例2的床面轮廓(单位：cm)

可以看出案例1中上游丁坝周围的侵蚀比案例2中更深。案例1和案例2中上游丁坝周围冲刷坑最大深度分别达到15和2cm左右。情形1中的沉积区域集中在下游丁坝的下游区域，这是因为该区域发生的速度和回流的减少。另一方面，在情形2中，沉积区分布在整个通道内，在下游丁坝下游浓度较小。

案例1和案例2沿渠道(y=40cm和y=72cm)的水位和床面纵向剖面如图3—4所示。

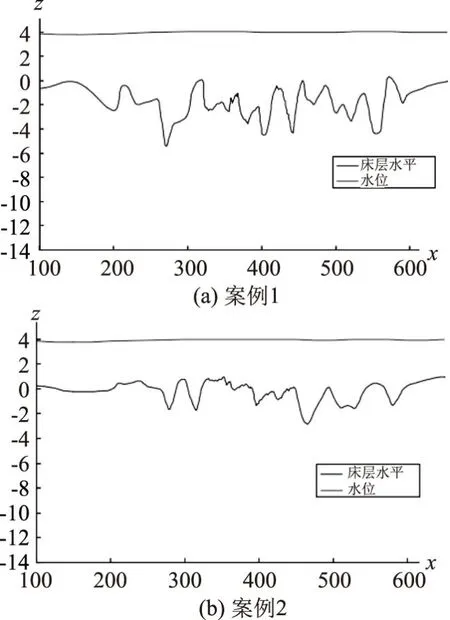
图3 案例1和案例2的主河道(y=40cm)沿程水面和床面纵剖面(单位：cm)

图4 案例1和案例2的主河道(y=72cm)沿程水面及床面纵剖面(单位：cm)

水平z=0cm表示初始床层高度。纵剖面y=40cm对应于水槽中心线，y=72cm对应于距渠道左壁8cm处的纵剖面。在这2种情况下，都可以看到丁坝附近水位的小幅上升，这可能是由于丁坝收缩水流宽度的影响。

2.2 数值结果与实验结果比较

图5—6分别给出了案例1在深度z=2.0cm时，不透水丁坝周围速度分布的实验结果和模拟结果。

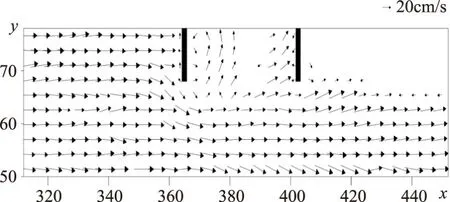
图5 案例1在z=2.0cm时xy平面丁坝周围的速度场(实验)(单位：cm)

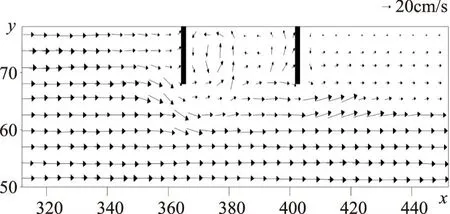
图6 案例1在z=2.0cm处xy平面丁坝周围速度场(模拟)(单位：cm)

模拟的速度大小与实验吻合较好。当水流接近上游丁坝时，阻塞流的大部分转向主槽，在丁坝坝头前方形成掺混区。一部分水流向下游流动，在丁坝间形成回流。将模拟结果与实验结果进行对比，发现在丁坝上游区域，流动结构较为相似，而在下游区域，流动结构存在一定的差异。与实验结果相比，模拟结果中观察到明显的回流流动。其中一个原因可能是测量网格过于粗糙，不利于实验的进行。

对于案例2透水丁坝周围速度场的实验和模拟结果分别如图7—8所示。

图7 案例2在z=2.0cm处xy平面内切槽周围速度场(实验)(单位：cm)

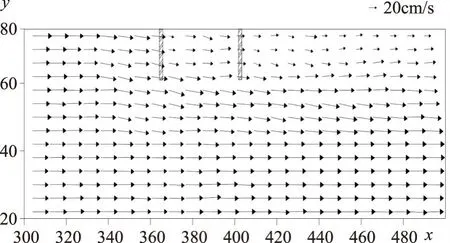
图8 案例2在z=2.0cm处xy平面丁坝周围速度场(模拟)(单位：cm)

在这种情况下，流动方向变化不大。可以看出，在实验结果中，刚经过上游丁坝后，流动方向转向右侧壁面。在上游丁坝的下游，流速发生了减小，但水流经过下游丁坝后，流速的减小变得更加显著。在下游丁坝可观测到的泥沙沉积，这可能是由这种流速降低引起的。与不透水丁坝相比，透水丁坝中的水流流态几乎平行于丁坝头部附近的河道。

实验和模拟结果在靠近上游丁坝处的yz平面内的速度矢量分别如图9—10所示。

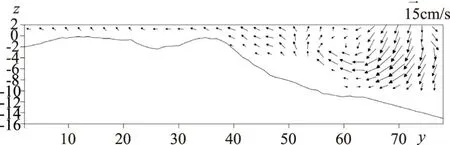
图9 案例1在x=362cm处yz平面丁坝周围速度场(实验)(单位：cm)

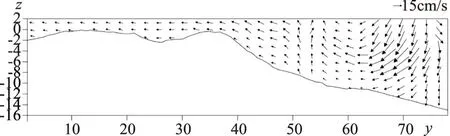
图10 案例1在x=362cm时yz平面丁坝周围的速度场(模拟)(单位：cm)

该断面纵向位置为x=362cm，正好位于上游丁坝上游2.25cm处，由下游向上游可见。从实验结果来看，上游丁坝附近的回流流动与计算结果非常相似。上游丁坝附近的床面冲刷可能是由于该回流的影响，在丁坝(从y=65cm到y=80cm)附近更为明显。这意味着水流正在侵蚀河岸。因此，在利用这种丁坝时，需要采取保护措施。与不透水丁坝的情况相比，透水丁坝的情况没有显示在这里，因为流过桩的水流在丁坝上游引起了少量的回流，没有造成明显的侵蚀。

3 结论

本研究表明在相同水力条件下，不透水丁坝引起的侵蚀明显比透水丁坝更为严重，这为丁坝的设计和施工提供了重要参考；通过数值模拟，能够较为准确地模拟固定床条件下丁坝周围的流动结构，这为类似工程的模拟和预测提供了可靠的工具；未来的工作将集中在进一步验证数值模型在可动床和淹没条件下的适用性，并将模拟结果与更多实验数据进行比较。此外，在实际应用中，需要综合考虑不同的环境因素和工程要求，以制定更为科学和可行的丁坝管理措施。这些工作将有助于更好地理解和管理丁坝周围的水动力环境，保护水利工程的可持续发展。