基于自适应滑模控制的下肢外骨骼机器人步态轨迹跟踪

张奕星

重庆交通大学，重庆 400060

0 引言

随着经济发展，中国逐步迈入老龄化社会。根据最新的第七次全国人口普查结果显示，全国60 岁及以上人口约为26 402 万人，占全国总人口的18.70%[1]。膝关节作为人体运动的主要部位，当其受到伤害时对日常生活的影响极大，为改善老年人以及下肢受伤人群的生活质量，下肢外骨骼机器人应运而生[2]。但是，目前国内的下肢外骨骼机器人功能单一且价格昂贵，因此，为我国下肢损伤患者提供价格低廉、适时有效、仿生性高的康复训练和辅助器具已经成为刻不容缓的重要课题。目前，下肢外骨骼机器人通常由电机、液压、气动3 种方式驱动。电机具有控制技术成熟、稳定高效的特点，但是其缺点也很明显：适用于外骨骼机器人的电机型号较少，且缺少驱动大负载的能力[3]；液压驱动则能够增强下肢外骨骼机器人的负载能力[4]，但这种驱动方式具有容易漏液[5]、运行过程中能量损耗大的缺点；气动驱动方式中以气动肌肉作为驱动源较为合适，因其具有密度高、质量轻、柔顺性好的特点，将其固定形成拮抗对拉，完成关节屈伸运动[6]，但其具有的高非线性和时滞性在控制方面是一个难题[7]。在现有的外骨骼机器人产品中，傅利叶公司的Fourier X1 与迈步公司的BEAR-H 由电机驱动[8]，液压驱动的则有HULC、XOS、DSME 等外骨骼机器人，以气动肌肉作为驱动源的外骨骼比较少，美国的密歇根大学使用气动肌肉作为踝关节的驱动源。

本文通过对使用者佩戴下肢外骨骼机器人进行康复运动的分析，设计了使用粒子群算法以人体膝关节瞬心轨迹为优化目标的双摇杆膝关节结构，然后对下肢外骨骼机器人进行3D 建模，设计了以气动肌肉驱动髋、膝关节的下肢外骨骼机器人，并且针对气动肌肉难控制的问题，采用了基于自适应模糊滑膜算法进行步态仿真，仿真效果表明，该算法具有良好的轨迹跟踪性能。

1 下肢外骨骼机器人结构设计

1.1 关节结构设计

由于人体穿戴下肢外骨骼行动时，由人体主动驱动进行负角度反向摆动[9]，所以膝关节选用了双摇杆结构，然后使用粒子群算法进行尺寸优化。

本文提出的气动肌肉驱动的双摇杆膝关节结构简图如图1 所示。图1（a）中，l1、l2、l3、l4分别为双摇杆关节4 根连杆，其中，l1连接大腿，l3连接小腿，θ为膝关节转动角度。图1（b）是由气动肌肉进行拮抗运动，带动双摇杆关节完成屈膝的运动简图。

1.2 关节尺寸优化

由于佩戴者在使用外骨骼机器人进行行走时，其膝关节瞬心是在变化的，所以以人体膝关节瞬心轨迹作为目标函数，使用粒子群算法对连杆尺寸进行优化。

人体膝关节的平面膝关节中心点数学描述如下[10]：

式中，F为屈膝角度；V为内翻角度；R为内旋角度；YDIS为Y轴方向位移量；ZDIS为Z轴方向位移量。

WALKER P S 等人[10]提出的描述膝关节运动的方程考虑了内翻和内旋对胫股关节矢状面运动的影响，其平面膝关节瞬心点是通过在矢状面上投影三维股轴运动得到其运动轨迹，如图2 所示。因为人体的膝关节瞬心轨迹是一条变化的曲线，所以需要设计一款变瞬心的膝关节下肢外骨骼机器人提升仿生性和舒适性。

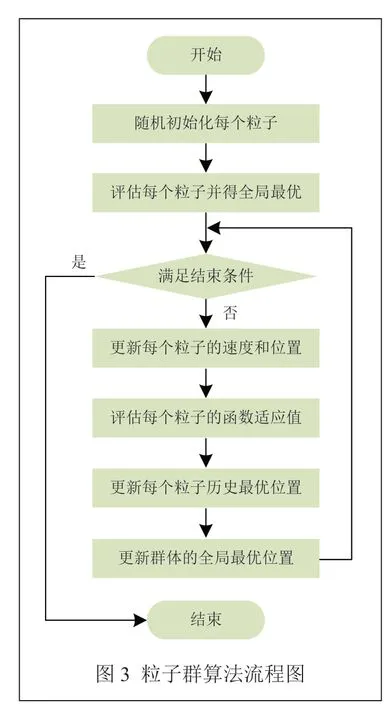
粒子群算法大致分为以下几步来进行优化：（1）初始化粒子群，随机生成初始位置和速度；（2）计算每个粒子的适应度值，更新个体历史最优位置和全局历史最优位置；（3）根据公式更新每个粒子的速度和位置；（4）如果满足终止条件，输出当前的最优解，否则返回第（2）步。通常情况下，终止条件可以设置为达到最大迭代次数，或者连续迭代中都没有发现更优的解等[11]。详细的算法流程如图3 所示。

设计变量是在优化过程中需要计算的未知量，选取人工膝关节中杆长l1、l2、l3、l4，并且双摇杆型人工膝关节应满足以下条件：（1）最短杆与最长杆的杆长长度之和小于等于其余两杆的杆长长度之和；（2）最短杆的对面杆为机架。此时约束条件如下：

利用粒子群算法对目标函数进行优化后，得到的双摇杆杆长尺寸如表1 所示。

表1 优化后连杆尺寸参数

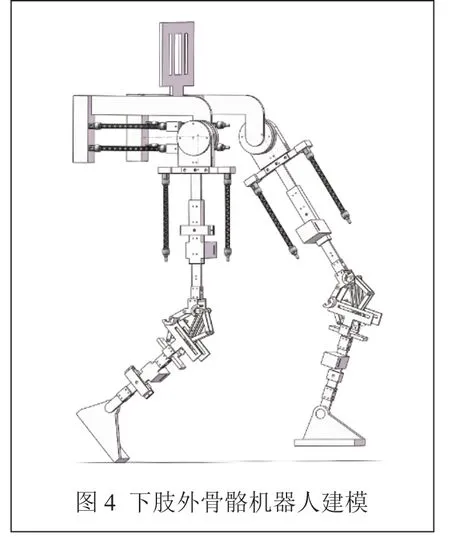
结合人体下肢参数与所设计关节，在SolidWorks中进行下肢外骨骼机器人3D 建模，如图4 所示。

2 控制器设计

滑模控制是一种简单的、适用于非线性系统的控制算法，在模型建立不精确的情况下，该算法也能够保证运动轨迹在有限时间内得到较好的跟踪效果[12]。自适应算法则是不断地接近模型的一种算法，该算法可以有效地弥补模型不精确的缺点。本文采用的自适应滑模控制算法对于下肢简化模型的轨迹跟踪具有优越的跟踪性能。

将下肢外骨骼机器人的单腿简化为一个双关节模型，其动力学模型为：

式中，H、C、G分别为外骨骼机器人的惯性矩阵、离心力和哥氏力、重力项；τ为外骨骼机器人的力矩；、分别为髋、膝关节转动的角加速度和角速度；q=[q1q2]，τ=[τ1τ2]，且

其中，q1、q2分别为髋、膝关节转动的角度；α、β、ε、η为常数。

式中，I1、Ie分别为髋关节与膝关节的转动惯量；m1、me分别为大腿小腿质量；l1、lc1、le分别为大腿长度、大腿质心到髋关节长度、小腿长度；σe为任意常数。

假设，α、β、ε、η为未知常数，取误差，定义：

滑模函数为：

设计控制器为：

由于H为正定矩阵，设计Lyapunov 函数为：

式中，Kd、ri为控制参数，于是：

将控制律代入得：

根据下肢外骨骼机器人动力学方程线性化特性，得到：

设计自适应律为：

3 仿真结果与分析

将三角函数作为髋、膝关节期望角度轨迹，输入到PID 控制算法与自适应滑模控制算法中进行对比，得到以下仿真结果。

图5 是三角函数作为输入到PID 控制器中进行仿真试验并且得到期望轨迹与仿真轨迹的误差，可以看出，PID 算法在波峰、波谷位置处的跟踪性能最差，整个跟踪过程中效果不好。

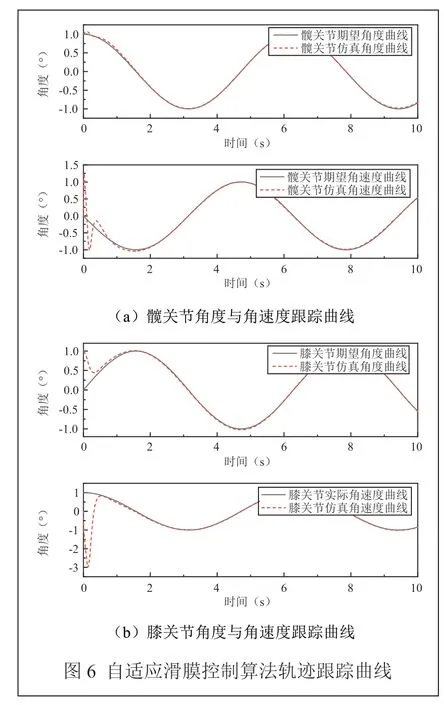
由图6（a）可以看出，在髋关节角度跟踪过程中，最大超调为0.12°，在1.32 s 时刻跟踪上角度曲线。而在角速度跟踪过程中，最大超调为1.23°，在2.3 s 时刻跟踪上角速度曲线。由图6（b）可以看出，膝关节角度跟踪过程中，最大超调为1.13°，在1.97 s 时刻跟踪上角度曲线，在角速度跟踪过程中，最大超调为-3.23°，在2.1 s 时刻跟踪上曲线。仿真结果表明，该算法具有良好的轨迹跟踪性能。

4 结束语

文章采用粒子群算法，以双摇杆关节为基础模型，将人体运动时膝关节瞬心轨迹变化曲线作为目标函数，优化其杆长，达到符合人体膝关节瞬心轨迹的目的，并在SolidWorks 中完成了下肢外骨骼机器人建模；然后采用了自适应模糊控制来进行仿真，并且使用PID 控制算法进行对比。仿真结果表明，自适应滑模控制具有良好的轨迹跟踪性能，与传统的PID 算法相比更具有优越性。