四阶时间分数波方程的快速紧致差分方法

王 婉，张海湘，杨雪花

（湖南工业大学 理学院，湖南 株洲 412007）

1 研究背景

分数微分方程现已被应用于越来越多的领域，如黏弹性材料[1-2]、控制理论[3]、金融市场中的期权定价模型[4-5]等。到目前为止，科研工作者们提出了很多解决具有弱奇异性分数阶微分方程的方法，比如有限差分法[6-7]、有限元方法[8-9]、光谱方法[10]，傅里叶变换法[11-12]等。对于分数阶微分方程中的Caputo导数项，学者们采用不同方法近似处理。例如，Xu D.等[13]用L1离散Caputo导数项，用二阶卷积求积公式近似Riemann-Liouville积分项，构造了紧差分格式，不仅给出了收敛性和稳定性的证明，且以数值算例验证了理论分析结果。Guo J.等[14]用L1-2公式离散Caputo导数项，用二阶有限差分法离散积分项，得知其空间收敛阶和时间收敛阶都达到二阶，并证明了格式的稳定性与收敛性。Shen J.Y.等[15]提出H2N2数值微分公式（二次Hermite和Newton插值多项式的应用）来近似Caputo导数项，并建立了有限差分格式。为了增加计算效率，其利用指数和近似核t1-γ，并推导出一种快速差分格式。对于初始时间的弱奇异性也在等级网格中进行了讨论。Jiang S.D.等[16]提出了分数扩散方程的快速L1差分格式，(0, 1)阶的Caputo导数项被快速L1递归公式离散。Xu W.Y.等[17]考虑一种具有二阶空间和时间精度的快速差分格式。用FL2-1σ公式近似时间卡普托导数，该公式使用了核指数和近似Caputo微分中出现的函数；通过离散能量方法证明了其无条件收敛性，最后通过数值例子验证了该方案的数值精度和效率。

本文讨论如下四阶分数波方程的初边值问题：

其初始条件和边界条件分别如下：

式（1）～（3）中：Ω=(0,L)×(0,T]；f(x,t)、u0(x)、ψ(x)为光滑函数；

本文中，C为一个正常数，在不同情况下可能具有不同的值。

2 预备知识

对区间[0,L]作M等分，区间[0,T]作N等分，记h=L/M,τ=T/N,xj=jh, 0≤j≤M,tn=nτ, 0≤n≤N，其中h为空间步长，τ为时间步长。

引理1[16]对于给定的α∈(0, 1)、截止时间限制δ、误差ε和最后时间T，有一个正整数Nexp，正点和相应的正权重，可得，其中

接下来介绍一种运用H2N2方法计算Caputo分数导数的快速算法。

令δ=τ/2，可得

其中，

引理2[15]设，γ∈(1, 2)，则有，。

其中

引理3[17]若函数，则有

3 数值离散格式

定解问题（1）～（3）可写成如下形式：

定义网格函数

将离散紧算子A分别作用于式（6）和（7），由泰勒展开式、引理1及2，可得

式（8）（9）中：

注意：初边值条件为

引理4由带积分余项的泰勒展开式及不等式（10），可得

4 紧差分格式分析

为了证明格式的收敛性，给出以下引理。

引理5[18]设u,v∈Vh，则

引理6[19]设u,v∈Vh，则有

引理7[20]设u∈Vh，可得

引理8[21]对于任意正整数p和函数G={G1,G2,…}，有

其中，{aj}定义见式（4）。

引理9[19]对任意网格函数，有

引理10[22]设F(k)、g(k)为非负函数，且满足

定理1设是问题（1）～（3）的解，是差分格式的解。为精确解，为数值解。则有

证明：令将式（8）（9）和（12）与（13）相减，得到如下误差方程：

将算子A作用在式（13）中第二个式子，可得

利用引理2和引理3，则有

用式（16）减去式（15），可得

由引理6可知

将式（18）和（19）相加，可得

对于式（21）右端的第一项，利用引理9和young不等式，且考虑η0=0，可得

式（21）右端第二项，利用young不等式，得到

将式（22）～（25）代入式（21），有

令

因而式（26）可写成

考虑式（10）和引理4可得

当m为任意值时，有

由式（14）和（17）知

引用引理7，有

定理1证毕。

5 数值算例

应用快速紧差分格式计算下列定解问题：

其中精确解为

右端项为

不同步长时的最大误差为

空间收敛阶为

时间收敛阶为

固定时间步长N=2 048，参数ε=10-12，γ取不同值时，差分格式的最大误差以及相应的空间收敛阶与CPU时间见表1。由表1中数据可知，上述问题的空间收敛阶为4。

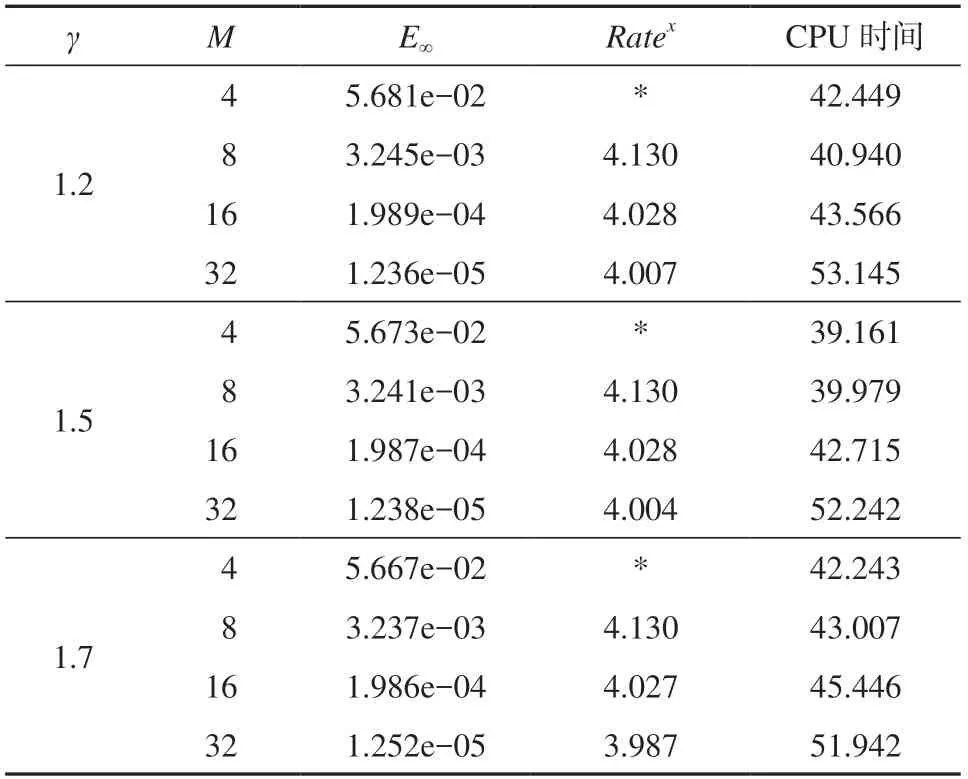
表1 N=2 048时最大误差及相应的空间阶、CPU时间Table 1 Maximum error, spatial order and CPU time with N=2 048

固定空间步数M=512，参数ε=10-12，表2中列出了不同γ取值和时间步长N下，计算得到的最大误差，及其相应的时间收敛阶与CPU时间。分析表2中的数据可以得知，时间收敛阶为(3-γ)阶，且所需CPU时间较少。

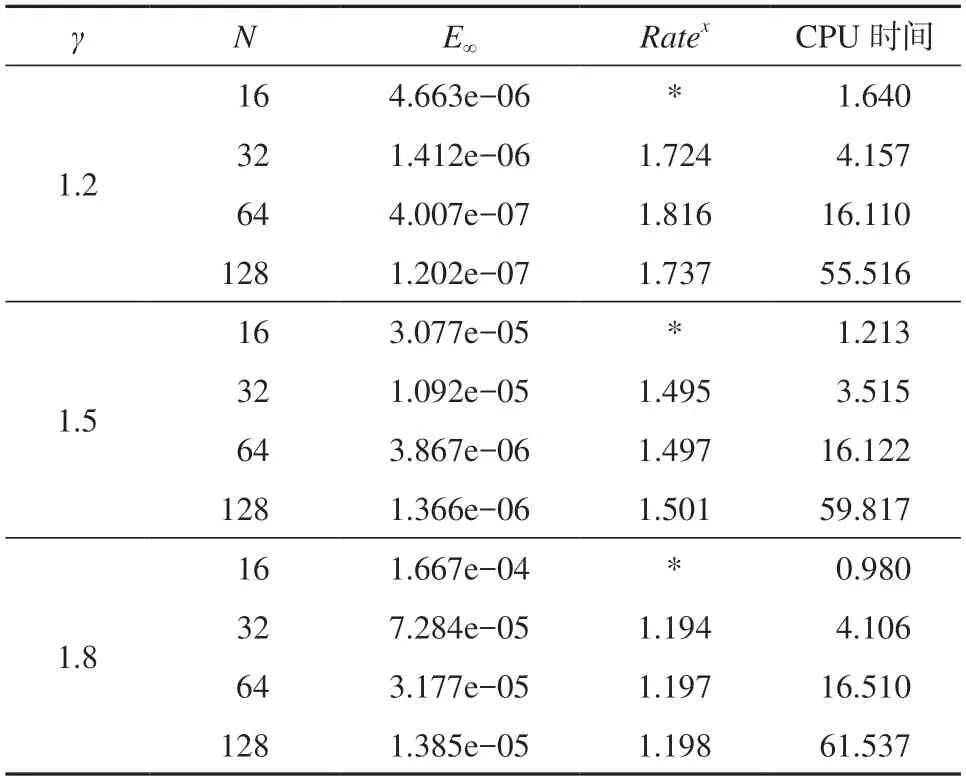
表2 M=512时最大误差及时间阶与CPU时间Table 2 Maximum error, time order and CPU time with M=512

固定γ值，图1给出了在空间方向上的收敛阶，图2给出了在时间方向上的收敛阶。由图1和2可看出，实例的空间收敛阶与时间收敛阶与理论分析得到的结论是一致的。

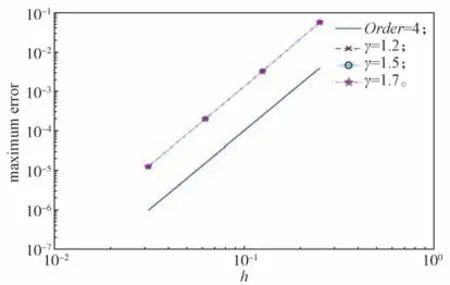
图1 当γ固定时的空间收敛阶Fig.1 Spatial convergence orders with a fixed value of γ

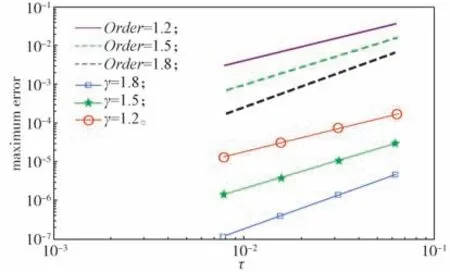
图2 当γ固定时的时间收敛阶Fig.2 Temporal convergence orders with a fixed value of γ

6 结语

本文研究了四阶分数波动方程的快速紧差分格式，Caputo导数项用一种快速的H2N2方法来近似，通过使用降阶法和离散能量法得到格式的收敛性。由数值算例可知，本文考虑的紧差分格式的收敛阶为O(τ3-γ+ε+h4)，且数值算例验证了理论分析结果。该格式所需的CPU时间较短。