采煤机截割部低照度图像的边缘检测技术

贾澎涛，靳路伟,*，王 斌，郭风景，李 娜

(1.西安科技大学 计算机科学与技术学院，陕西 西安 710054；2.陕西建新煤化有限责任公司，陕西 黄陵 727300；3.陕西陕煤蒲白矿业有限公司，陕西 渭南 715517)

采煤机作为开采煤矿资源的关键设备之一，其设备健康状态直接影响采煤效率及煤矿安全。采用视觉识别技术对采煤机截割部进行轨迹识别以避免故障的发生是当前研究的热点。在采煤机的运行过程中，由于矿井复杂的地质条件，常常会导致采煤机截割部偏离预设轨迹而碰撞煤岩引发故障。通过对采煤机截割部进行边缘检测，可以帮助识别其运行轨迹，从而及时对其运行轨迹进行纠偏，提高采煤机运行的安全性和可靠性。因此如何准确地检测采煤机截割部边缘成为确保采煤机安全运行的关键技术[1-2]，但是井下复杂的多尘、低照度环境，对采煤机的边缘检测提出了挑战。

目前常用的边缘检测方法主要有整数阶微分和分数阶微分方法，其中整数阶微分又可以分为一阶整数微分算子和二阶整数微分算子。一阶整数微分算子包括Roberts 算子、Prewitt 算子以及Sobel 算子等，二阶整数微分算子包括Laplacian 算子、LOG 算子。但是常用的一阶微分算子所检测的边缘往往较粗、不够精细；二阶整数微分算子虽然对梯度信息更加敏感，可以得到较细的边缘，但同时也放大了噪声信息。由于分数阶微分具有对噪声不敏感且所提取边缘较为精细的特点，逐渐成为了学者研究的热点[3-7]。

分数阶微分是整数阶微分的一种扩展。为了提高整数阶微分算子检测精度，学者们陆续提出了基于Grünwald-Letnikov 的改进分数阶微分算子[8]、与Otsu 阈值相结合的分数阶微分算子[9]、自适应的分数阶算子[10]、与灰色理论相结合的分数阶微分算子[11]等，逐步地提高了图像边缘检测的精度。但在对含噪、低光照图像进行边缘检测时，上述这些方法提取的图像边缘信息效果较差。

为了提升分数阶微分算子的抗噪性和鲁棒性[12-15]，学者们提出了高阶Caputo-Fabrizio 分数阶微分掩膜算子[16]、彩色图像分数阶微分算子[17]、改进的分数阶Sobel 算子[18]等，在提升图像对比度或抗噪性方面都有一定的效果，但仍存在边缘缺失、细节模糊等问题。因此，针对低照度条件下采煤机设备的边缘检测需求，提出了一种基于局部特征的分数阶微分图像边缘检测Lif 算法，在有效提取图像边缘信息的同时能够保留更多的纹理细节信息并较好地抑制图像中的噪声，为后期的采煤机截割部边缘识别奠定了基础。

1 基础理论

分数阶微分可以对非整数阶的导数进行描述，其函数在局部区域内呈现出连续但非光滑的特性。使用分数阶微分算子进行边缘检测任务时，通过调整分数阶微分算子的参数，可以在图像中捕捉不同尺度的边缘信息，从而使提取的图像边缘更为精细、清晰且包含更多的纹理细节。

分数阶微分有3 种不同的定义方式：G-L 定义[19]、R-L 定义以及Caputo 定义[20]。G-L 定义相对其他的微分定义更为精确，因此成为最常用的一种非整型分数阶微分定义，G-L 分数阶微积分表达式为：

其中，伽马函数 Γ(n)为：

2 基于局部特征的分数阶微分算子构造

2.1 算法思想

基于局部特征的分数阶微分图像边缘检测Lif 算法的思想为：首先，按照分数阶微分的定义构造相应的微分掩膜算子。然后，根据Pascal 三角形理论推导出掩膜算子每个位置所对应的权重系数，考虑到图像中不同方向的边缘信息，还将掩膜算子扩展到0°、90°、45°、135° 4 个方向上，使所构建的掩膜算子可以全面地捕捉图像中的边缘信息。最后，得到不同方向上的算子卷积结果后，对每个结果进行基于局部信息的后处理操作，使算子可以根据局部信息自适应地调整输出像素值，从而在处理井下等低照度图像时具备更强的抗噪性，并保留更多的纹理细节信息。

2.2 算法描述

在设计Lif 算法时，首先构造相应的分数阶微分掩膜算子并将其扩展到不同的方向上。根据分数阶微分的定义，将其对应的一元a阶微分表达式扩展到二维，得到二维分数阶微分的差分表达式，因此，0°方向左侧上的表达式为：

根据以上条件可得0°方向右侧上的表达式为：

因此，将式(3)及式(4)相加，可得0°方向上左右两侧的表达式为：

同理，将分数阶微分推广到其余方向上，可得90°方向上左右两侧的表达式为：

45°方向上左右两侧的表达式为：

135°方向上左右两侧的表达式为：

根据以上表达式，可得到每个方向上的分数阶掩膜算子，以0°、90°方向上为例，如图1、图2 所示，其中，图1、图2 中掩膜算子相应位置系数与上述表达式的系数一一对应。

图1 0°方向分数阶掩膜算子Fig.1 Fractional mask operator in the 0° direction

图2 90°方向分数阶掩膜算子Fig.2 Fractional mask operator in the 90° direction

构造分数阶微分掩膜算子之后，然后利用Pascal三角理论推导出掩膜算子各位置的相应权重。平滑函数为：

对应的差分函数为：

其中，函数：

根据上述平滑函数和差分函数可得相应的最优平滑算子和最优差分算子，如图3 所示，不同模板尺寸对应不同的模板系数，所设计算法采用的模板尺寸为5×5。

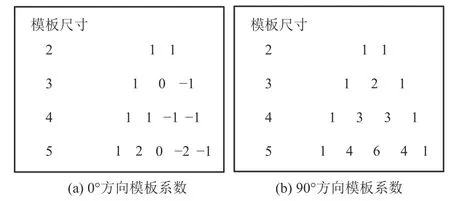
图3 最优平滑算子以及最优差分算子Fig.3 Optimal smoothing and difference operators

最终的微分模板相应位置的权重推导公式为：

同样以0°、90°方向为例，由式(12)可得到相应位置的模板系数如图4 所示。

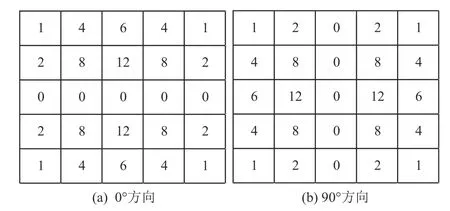
图4 0°和90°方向的微分模板系数Fig.4 Differential template coefficients in 0° and 90° directions

将每个方向上的掩膜算子与相应的模板系数相乘，可以得到对应方向上的最终掩膜算子。其他方向的掩膜算子由0°、90°方向算子旋转对应角度得到，不同方向上构造的分数阶掩膜算子如图5 所示。

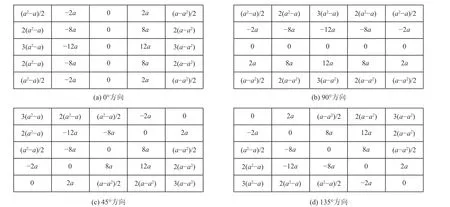
图5 各方向分数阶掩膜算子Fig.5 Fractional mask operators in various directions

2.3 基于局部特征的自适应后处理

在得到最终的掩膜算子后，用每一个掩膜算子模板的系数与输入窗口的对应的像素值进行相乘，会得到输入窗口在每一个方向上的微分结果，分别为：W1、W2、W3、W4；得到4 个不同的值后分别再对每个值进行下列运算，微分结果为：

其中，*代表卷积，分母的设计使算子根窗口的局部信息自适应调整最后的输出像素值，当待检测像素点位于图像中较为平滑的区域时，分子近乎为0；而当待检测像素点位于图像中的边缘区域时，分母可以动态地放大该像素点的输出。最后分别引入两个系数，∝使得算子可以对低照度图像中的边缘信息更加敏感，而Q则可以减小噪声的影响。经实验表明，参数 ∝ 以及参数Q分别设置成3 和1 000 时效果最佳。

经过如上运算得到每个方向的输出像素后，对这4 个不同方向的像素值取最大值，得到最终的像素值为：

3 实验及结果分析

为了检验所提Lif 算法的有效性，分别从视觉效果分析和客观指标分析两个方面进行对比实验，所对比算法分别为：Sobel 算法、Laplacian 算法、Tiansi 算法、文献[11]算法以及文献[18]算法，实验环境为Python3.9。

3.1 实验数据

进行对比实验时，实验数据来自于煤矿井下生产过程中的采煤机截割部设备监测视频，视频时长约为20 min。采煤机图像如图6 所示，图像尺寸均为512×512 像素，其中，图6a 与图6b 分别为不同角度下采煤机截割部设备监测视频所提取的关键帧示例，图6a 中包含较多的采煤机截割部细节纹理信息，且边缘信息较为清晰，图像质量相对较好；图6b 的图像质量较差，背景边缘信息和目标边缘信息不容易区分。为了验证Lif 算法的有效性及泛化性，在图6a 与质量较差的图6b上同时进行对比实验。

图6 低照度采煤机图像Fig.6 Low illumination shearer images

3.2 实验步骤

实验整体步骤如图7 所示。

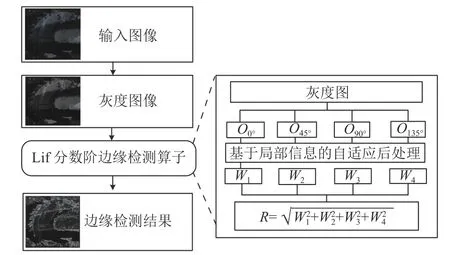
图7 基于局部特征的分数阶微分边缘检测算法流程Fig.7 Flowchart of fractional differentiation-based edge detection based on local features

步骤一，将原图像转换为相应的灰度图像。

步骤二，得到灰度图像待处理的像素点信息后，将像素点所对应的局部窗口分别与4 个不同方向上的分数阶微分掩膜算子进行卷积微分操作。

步骤三，在每个方向上都进行微分操作后，再分别进行基于局部信息的自适应后处理，获得每个方向相应的微分结果W1、W2、W3、W4。

步骤四，对步骤三中的微分结果值进行相应运算，得到最终的像素结果R。

3.3 视觉效果及分析

经各算法处理所得到的图像边缘分别如图8、图9所示。图8a、图9a 为经过Sobel 算子处理后的结果；图8b、图9b 为经过Laplacian 算子处理后的结果；图8c、图9c 为经Tiansi 算子处理后的结果；图8d、图9d 为经文献[11]算法处理后的结果；图8e、图9e 为经文献[18]算法处理后的结果；图8f、图9f 为本文所提Lif 算法的处理结果。

图8 图像1 边缘提取效果对比Fig.8 Comparison of Image 1 edge extraction effect

图9 图像2 边缘提取效果对比Fig.9 Comparison of Image 2 edge extraction effect

分析图8、图9 的边缘检测结果可得知，使用Sobel 算子进行边缘检测后，只检测出了部分边缘信息，并且丢失了大量图像的细节，边缘结果比较模糊；而Laplacian 算子的检测结果相对其余算子相差很多，肉眼无法有效地识别边缘信息；使用Tiansi 算子以及文献[11]算法进行边缘检测的结果虽然大致轮廓比较清晰，但是对于较暗、弱小的边缘以及一些细节信息并未检测出来；文献[18]算法虽然检测出了一些较暗、弱小边缘并保留了部分细节纹理信息，但是边缘较为模糊且不连续，保留的细节纹理信息也不够完整；从图8f、图9f 中可以看出，经Lif 算法处理得到的图像边缘细节特征丰富完善、整体轮廓清晰明亮，富有层次感，并且将原图中较暗、弱小的边缘较完整地检测出来。

3.4 客观指标及分析

实验中使用信息熵(Entropy)、平均梯度(Average Gradient，AG)以及结构相似度(SSIM)作为对上述两幅图像各种边缘检测结果图的客观评价指标。Entropy 是图像质量评价的常用指标，它从信息论的角度反映图像信息丰富程度。通常情况下，图像信息熵越大其信息量就越丰富，质量越好；平均梯度AG 是指灰度变化率的平均值，反映了图像的纹理变化情况以及清晰度，一般来说平均梯度越大说明图像的质量越好；SSIM 用来衡量两幅图像的相似度，SSIM 值越大则表示两张图像越相似，图像处理的效果越好。

对比表1、表2 中的客观指标，本文Lif 算法在3 个客观指标的对比中都为最优，且Entropy 以及AG指标获得了大幅度的提升，Entropy 指标分别高于Sobel算法、Laplacian 算法、Tiansi 算法、文献[11]及文献[18]算法99%、190%、105%、43%、11%；在AG 指标上分别高于上述算法429%、238%、76%、23%、23%；在SSIM指标上分别高于上述算法56%、138%、89%、152%、6%，证明了本文所提Lif 算法的有效性。

表1 图像1 指标对比Table 1 Comparison of indexes for Image 1

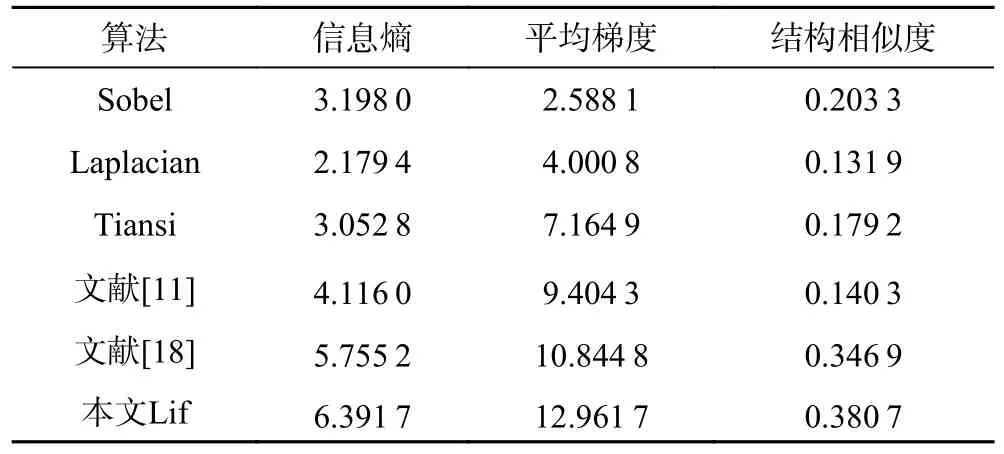
表2 图像2 指标对比Table 2 Comparison of indexes for Image 2

4 结论

a.构造了一种基于分数阶微分的边缘检测Lif 算法，使其既能保证边缘轮廓清晰又能检测出更多的细节纹理信息，解决了针对井下等低照度图像进行边缘检测时，检测效果差、轮廓不清晰的问题。

b.所提Lif 算法用图像的局部信息对原始图像的边缘检测结果进行自适应的后处理，实验结果表明，Lif 算法与常见的边缘检测算法相比，边缘轮廓更加清晰明亮且细节特征丰富，同时客观评价指标也均获得了较大的提升，因此，Lif 算法可以有效地进行井下低照度图像的边缘检测任务。

c.通过对井下等设备的边缘检测实践显示，Lif 算法的应用可以有效地支持复杂环境下的设备检测、轨迹识别等任务，提高了井下工作的安全性、效率和可靠性。此外，由于Lif 算法可以更准确地捕捉图像中的边缘信息，因此对于常规环境下的边缘检测同样具有适用性，能够取得较好的检测结果。

d.本文所提算法虽然获得较好的检测性能，但由于加入了基于局部信息的后处理操作，故计算量和占用内存量也相应增加。下一步将会在保证检测性能的基础上，开展减少运算量以及占用内存量的研究。

符号注释：

a为分数阶阶次，a＞0；G 为G-L 分数阶微分定义的缩写；Gm为0°方向上的最优平滑算子系数；Gn为90°方向上的最优平滑算子系数；h为微分步长；Hm为0°方向上的最优差分算子系数；Hn为90°方向上的最优差分算子系数；k为模板的尺寸；l 为左方向；m为多项式对应的项数；n为多项表达式中对应的项数；O0°、O90°为微分模板相应位置权重；p为模板窗口各个点的位置；r 为右方向；R为算子最终输出像素值；s为输入灰度图窗口；t为分数阶微分的上限；u为分数阶微分的下限；W为图像窗口与掩膜算子的卷积结果；W1、W2、W3、W4分别为图像窗口与4 个不同方向上掩膜算子的卷积结果；f(x,y)为二维图像强度函数；(x,y)为图像中相应的位置；K(x,y)为组合数函数；ωi为每个方向上的掩膜算子；∝、Q均为调整参数。