基于SSA-CG-Attention 模型的多因素采煤工作面涌水量预测
2024-04-28丁莹莹尹尚先连会青李启兴祁荣荣卜昌森夏向学李书乾
丁莹莹,尹尚先,*,连会青,刘 伟,李启兴,祁荣荣,卜昌森,夏向学,李书乾
(1.华北科技学院 河北省矿井灾害防治重点实验室,北京 101601;2.吉林大学 建设工程学院,吉林 长春 130026;3.中国矿业大学(北京) 地球科学与测绘工程学院,北京 100083)
煤矿开采过程中,工作面涌水是威胁矿井安全生产的主要因素之一[1-2]。通过预测工作面的涌水量,可以提前了解工作面涌水情况,减少矿井发生灾害的风险,保障矿工的生命安全[3]。因此,提高矿井工作面涌水量预测精度至关重要。
矿井涌水量预测是对整个矿井的涌水情况进行预测,这种预测研究较为常见[4]。刘慧等[5]运用时间序列预测模型对矿井涌水量进行预测,但该研究仅考虑涌水量数据,忽略了其他因素的影响。熊鹏等[6]利用数值模拟方法对矿井涌水量进行预测,但由于预测范围较广,出现了数据量不足、复杂性增加、干扰因素增加等问题,导致预测精度较低。因此,对矿井工作面涌水量的预测更具精确性和针对性。
目前常用的涌水量预测方法包括统计方法[7]、数值模拟方法[8]和人工智能方法[9]等。王档良等[10]运用统计方法对涌水量进行预测,该方法简单易行,但对数据及操作人员依赖性很强。侯恩科等[11]利用数值模拟方法对矿井水文地质条件分析和模拟,并预测涌水量。但数值模拟需要大量观测数据和高精度地质信息,模型概化地质原型的程度决定预测的精度,预测偏差较大。涌水量数据是典型的时序数据,长短时记忆网络是处理时序数据的主要模型[12]。吴卫忠等[13]利用人工智能方法建立时间序列模型对涌水量进行预测,具有运算速度快、适应性强的特点,但仅利用涌水量历史数据进行研究预测,精确度低且稳定性弱。王晓蕾[14]针对涌水量预测研究,提出应当建立多因素综合模型,扩展传统的单一模型的建议。但现阶段研究中较少有将多因素模型运用到涌水量预测领域的成果报道。
微震监测技术在煤矿突水监测预警中的应用已非常广泛,其在预测涌水量方面也发挥了重要作用[15]。微震监测系统能够实时监测底板断层和裂隙带的发育情况,确定断层尖端的扩展情况,从而为预测涌水量提供了重要依据[16]。微震监测数据可以反映出地下岩体的应力状态和破裂活动,这些因素与涌水量的变化密切相关,当微震能量增大,岩石破裂增强,导水裂隙带更发育,导致涌水量的增加[17],例如,陕西亭南煤矿具有完善的水情监测系统,结合矿井实际监测情况可以确定水害风险监测指标,并指出在顶板发生突水过程中,含水层水位、工作面涌水量以及顶板导水裂隙带发育高度在极短时间内都发生了较大的变化,这些变化与微震数据的变化密切相关[18]。此外,微震数据还可以与其他监测数据结合,如水位数据,来提高预测的准确性,通过对水位和能量数据的监测分析,可以有效地预测涌水量的变化趋势,这种方法已经被证明在实际应用中是可行的[19]。
基于以上研究,笔者结合微震数据和钻孔水位2 个特征因素,提出SSA-CG-Attention(Sparrow Search Algorithm-Convolutional Neural Network,Gated Recurrent Unit-Attention)模型。其中卷积神经网络(Convolutional Neural Network,CNN)用于提取非线性特征,门控循环单元(Gated Recurrent Unit,GRU)用于捕捉序列信息,Attention 用于加强对重要信息的关注,麻雀搜索算法(Sparrow Search Algorithm,SSA)用于优化参数。将微震能量数据和钻孔水位作为特征变量输入到SSACG-Attention 模型中,可以更全面地考虑工作面涌水量的关联因素,从而提高预测的准确性和稳定性,以期为工作面采取相应的排水措施提供依据,有利于保障工作面的安全。
1 模型结构
1.1 CNN 框架
卷积神经网络(Convolutional Neural Network,CNN)是深度学习的重要组成部分,不仅具有良好的自主学习能力,而且能够有效提取局部特征,具有较强鲁棒性,相较于传统算法,其表现更加优异[20]。本文模型中CNN框架用于自动提取矿井水害参数的内部特征。采用两层一维卷积层提取微震能量数据、水位数据的非线性局部特征,中间使用最大池化层对提取到的微震能量数据和水位数据的特征压缩并生成更重要的特征信息。经典的卷积神经网络由卷积层、池化层和全连接层等[21]组成,典型的CNN 基本结构如图1 所示。
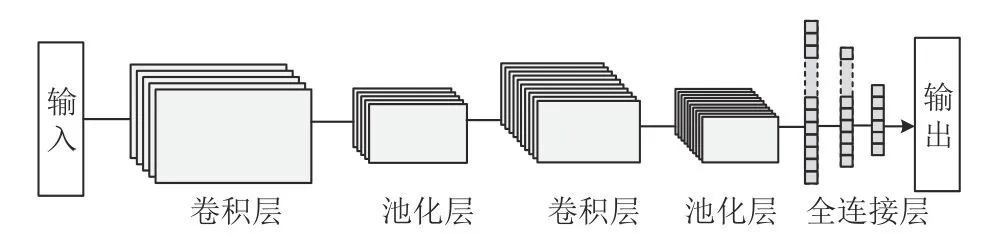
图1 经典CNN 的基本结构Fig.1 Basic architecture of a typical Convolutional Neural Network
池化层可以有效地缩小参数矩阵的尺寸,从而减少最后连接层中的参数数量。池化层输出大小的计算公式如下,本模型在每个池化窗口内取最大值。
1.2 GRU 隐藏层
门控循环单元(GRU)是一种常用的循环神经网络模型[22],既能够保证信息传递,也可以更好地处理长时序列数据,既可以用于单变量预测,也可进行多变量预测。本文模型构建GRU 时序特征层,学习通过CNN框架提取出的局部特征的内部动态变化规律,迭代提取更复杂的全局特征。GRU 是循环神经网络的一种,主要特点在于引入了重置门和更新门,重置门用于控制是否保留上一时刻的状态,更新门用于控制是否更新当前时刻的状态[23]。GRU 结构单元如图2 所示。
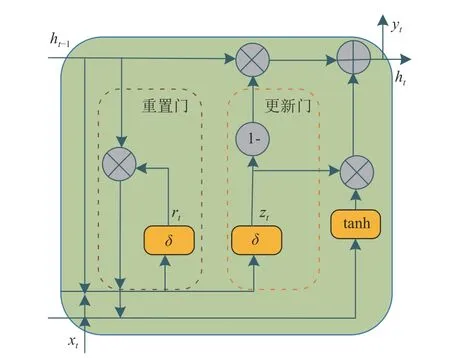
图2 GRU 结构单元Fig.2 Structural unit of the Gated Recurrent Unit
1.3 Attention 模块
注意力机制是一种能够处理输入序列并产生单个输出的序列到序列模型[24-25]。本文模型利用注意力机制自动对GRU 隐藏层所提取到的时间信息通过加权的方式进行重要程度区分,能够有效减少丢失历史信息,并突出关键历史时间点的信息,以削弱冗杂信息对涌水量预测结果的影响。可以更有效地利用涌水量数据自身的时间序列属性,挖掘深层次的时间相关性,本文模型将注意力权重数量设置为50 以控制模型的性能和复杂度。Attention 单元结构如图3 所示。

图3 Attention 单元结构Fig.3 Unit structure of the Attention mechanism
1.4 SSA 算法
SSA 是一种新型的群体智能算法,以麻雀的捕食策略为基础,通过仿真麻雀在寻找食物时的行为寻找最优解[26-27]。主要步骤为:初始化种群、适应度计算、更新位置、保存参数、判断终止条件。根据实验得到超参数趋于稳定的迭代次数,设置为终止条件。
更新位置时分为3 种情况:
(1) 更新适应度靠前麻雀的位置,即发现者的位置:
(2) 更新适应度靠后麻雀的位置,即跟随者的位置:
(3) 更新部分麻雀位置,即警戒者的位置:
使用SSA 搜索全局最优解,收敛速度更快,收敛能力更高,算法简单易用,需要迭代次数更少。
1.5 SSA-CG-Attention 模型构建
本文基于以上4 个模块提出一种基于SSA-CGAttention 模型的矿井工作面涌水量多因素预测方法,具体实现流程如图4 所示。
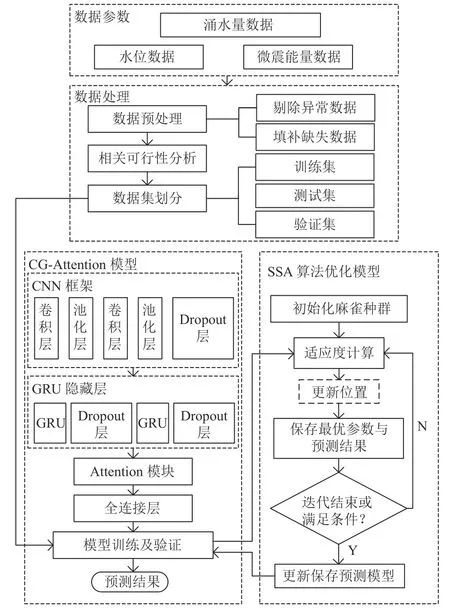
图4 SSA-CG-Attention 模型流程Fig.4 Flow chart of the SSA-CG-Attention model
模型的构建过程主要包括以下步骤:
(1)数据处理与划分。将采集到的水位数据、微震能量数据以及涌水量数据进行预处理,并划分数据集。其中数据的70%作为训练集,15%作为验证集,15%作为测试集。
(2)构建CG-Attention 模型。主要由CNN 框架和GRU 隐藏层融合形成新的网络结构。两类结构间加入随机失活(Dropout)层防止过拟合现象的同时,还可以提升模型的泛化性,并且减少模型的训练时间,本模型中drop 值为0.2。最后通过全连接层将前面提取的特征,经过非线性变化,提取这些特征之间的关联,最后输出最终涌水量预测结果,其核心操作就是向量乘积。
CG-Attention 模型的模型结构如图5 所示。
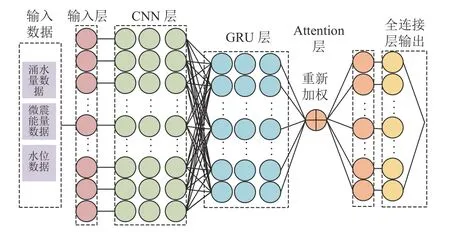
图5 CG-Attention 模型结构Fig.5 Structure of the CG-Attention model
(3)参数优化。采用麻雀搜索算法(SSA)更新模型各层的网络参数。本模型中使用验证集的均方差(EMS)为适应度函数,作为判断优化程度的标准,适应度fi计算公式如下:
(4)结果输出。通过评价指标对模型验证集验证寻优输出预测结果。
2 研究区概况及数据来源
2.1 充水条件
亭南煤矿位于黄陇侏罗纪煤田彬长矿区中部,陕西省咸阳市长武县亭口镇。207 工作面位于矿井北部二盘区中部,所采煤层为侏罗系延安组4 煤,煤层上覆含、隔水层自上而下为:第四系松散层孔隙含水层,平均层厚93 m;白垩系下统宜君、洛河组孔隙-裂隙承压含水层组,平均层厚280 m;中侏罗统安定组隔水层,平均层厚34 m;中侏罗统直罗组孔隙-裂隙承压含水层组,平均层厚11 m;中、下侏罗统延安组孔隙-裂隙承压含水层组,平均层厚13 m。
参照工作面内ZK8-1、3-1 号钻孔(表1),207 工作面4 煤顶板至洛河组底界距离173~182 m,回采后导水裂隙带沟通洛河组。洛河组含水层岩性主要以中粒砂岩、粗粒砂岩和粗砾岩为主,渗透系数为0.024 1 m/d。虽然渗透性及富水性均较弱,但巨厚含水层静储量丰富,导致工作面涌水量居高不下,起伏剧烈。

表1 207 工作面钻孔地层厚度数据Table 1 Thicknesses of strata in boreholes along the mining face 207 单位:m
2.2 数据来源
数据来源于陕西某煤矿207 工作面,针对微震能量数据、水位数据和涌水量数据进行研究。收集整理了2017-2019 年数据,其中,水位数据来自该工作面白垩系洛河组3-1 观测孔,该观测孔距离工作面最近且数据最全;微震数据由覆盖整个207 工作面作业区域的1 个监测探头和4 个拾震器获取得到。使用线性插值补齐缺失数据,具体的微震数据、水位数据与涌水量数据及其关系如图6 所示。

图6 微震能量、水位与工作面涌水量关系Fig.6 Relationships of microseismic energy,water level,and mine water inflow
2.3 相关性可行性分析
评价相关性常用的方法有皮尔逊相关系数、斯尔曼(Spearman)相关系数和肯德尔相关系数[28]。Spearman相关系数为r(p)的形式,r为相关性系数,p为显著性水平,相关系数范围为-1 到1,数值越接近-1 或1,表示相关性越强;显著性水平表明了相关系数的显著性,p值小于预设的显著性水平时,认为两个变量之间存在显著的相关性;否则认为两个变量之间无显著的相关性。本文使用SPSS 对涌水量、微震能量和水位数据进行Spearman 相关性分析。相关系数见表2。

表2 微震能量、水位和涌水量数据Spearman 相关系数Table 2 Spearman correlation coefficients between microseismic energy,water level,and mine water inflow
实验数据中,水位和涌水量之间的相关性系数为0.708,且显著性水平小于0.01,说明水位和涌水量之间存在显著相关性。涌水量和能量级之间的相关性系数为0.534,且显著性水平小于0.01,说明二者之间存在显著相关性。
对图6 微震能量、水位和工作面漏水量数据趋势分析如下:
(1) 2017-12-05-2018-02-20 期间,工作面处于底板应力变化剧烈及导水通道扩展、发展期。这一阶段水位变化幅度较小,涌水量相对稳定,微震事件能量级整体处于较低水平。
(2) 2018-02-28-2018-07-30 期间,矿压影响逐步增强,水位下降、水量增加,且微震事件能量级变化趋势与涌水量变化趋势基本吻合,微震事件能量级整体处于较低水平。2018-03-25 微震能量增大,能量级为1×105,涌水量剧增至769 m3/h,水位下降幅度也比较明显。
(3) 2018-08-31-2018-11-06 期间,矿山应力剧烈变化,引发地下水再度活跃,水位下降,水量增加。2018-09-15 微震事件能量级开始突增,形成第一个高峰,能量级达到6.4×105[29]。
由以上分析可得,钻孔水位和微震能量与涌水量密切相关。因此,将钻孔水位和微震能量数据作为涌水量预测的两个特征因素预测涌水量具有可行性。
2.4 模型评估
为了更好地评估预测结果,本文采用平均绝对误差(EMA)、均方根误差(ERMS)以及平均绝对百分比误差(EMAP)作为模型评价指标[30-31]。EMA用来衡量模型预测值与真实值之间的平均差异,值越小,说明模型的预测效果越好。ERMS是一种用于度量预测值与真实值之间误差的指标,值越小,说明预测值与真实值之间的误差越小。EMAP用来计算百分比误差,值越小,表示预测模型的准确性越高。计算公式如下:
3 实验结果与分析
3.1 各模型预测结果对比
将本文SSA-CG-Attention 预测模型和随机线性规划模型(Stochastic Linear Programming,SLP)、多层感知机(Multilayer Perceptron,MLP)、回归预测模型(Support Vector Regression,SVR)、GRU、长短期记忆网络(Long-Short Term Memory,LSTM)模型在该数据集上进行对比实验,得到结果如图7 所示。

图7 各模型预测结果Fig.7 Predicted results of various models
模型评价指标结果见表3。由表3 可以看出:SSACG-Attention 预测模型的EMA、ERMS和EMAP这3 个评价指标均优于SLP、MLP、SVR、GRU、LSTM 模型;组合麻雀搜索算法寻找最优超参数,GRU 和LSTM 模型的预测精度均有所提升,但CG-Attention 模型的提升效果最优;SSA-CG-Attention 模型预测涌水量的ERMS仅为7.25 m3/h,比MLP、SLP、SVR、LSTM、GRU 以及SSA优化的LSTM 和GRU 模型,分别降低了19.44、18.15、11.91、7.57、7.18、6.58、2.73 m3/h,进一步验证了提出的SSA-CG-Attention 预测模型的有效性和优越性。

表3 各预测模型评价指标结果Table 3 Results of evaluation indicators for each prediction model
3.2 多因素与单因素模型预测结果对比
矿井涌水量预测一般分为两类,一类是单因素预测,使用历史观察数据,学习历史数据特征进行预测。另一种是多因素预测,使用矿井水害数据进行预测。本实验选取传统的BP 神经网络与典型的时间序列模型LSTM和GRU 网络,分别对同一时间内仅使用涌水量数据进行单因素模型预测,与使用钻孔水位数据以及微震能量数据的多因素模型预测对比实验,结果见表4。
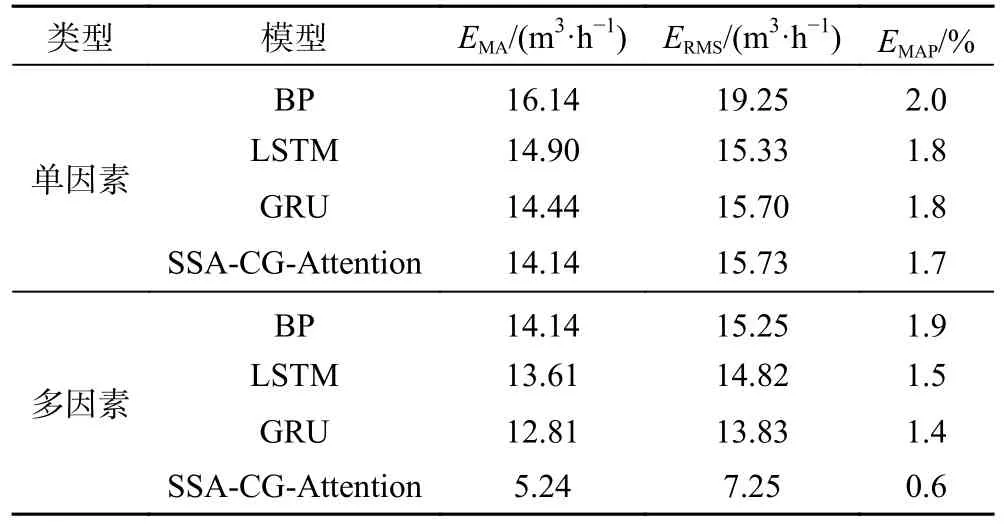
表4 多因素、单因素预测模型评价指标结果Table 4 Results of evaluation indicators for multifactor and single-factor prediction models
由表4 可以看出,多因素预测模型评价指标较优于单因素预测模型。这是因为使用涌水量历史数据预测结果仅考虑了历史趋势和变化规律,仅能提供单一时间序列信息,容易出现误判和漏判。而使用钻孔水位和微震能量数据预测工作面涌水量,多因素输入互为约束,信息获取更全面,结果输出更稳定、更准确,可以大大降低误报漏报概率,提高工作面涌水量预测可靠性、准确性。
3.3 多因素与单因素模型稳定性对比
将同一时间内涌水量历史数据与使用钻孔水位和微震能量数据拆分为训练集和测试集,并使用训练集训练模型。将测试集应用于训练完成的模型,并记录每个模型的结果。进行多次拆分和应用模型的迭代,以减少随机性,提高结果的准确性。分析每次迭代的结果,并计算每个模型的评估指标方差和D。计算公式如下:
将数据集进行20 次拆分迭代,进行预测实验获取方差结果见表5。

表5 模型评估方差Table 5 Variances for model assessment
由表5 可以看出,多因素模型的方差和普遍较小,因此,多因素模型一般比单因素模型预测结果更稳定。
4 实验验证
为确保新工作面的数据与已验证模型的数据具有相关性,同时保证数据的质量和完整性良好,选取同矿区相邻401 工作面的数据进行多因素涌水量预测模型验证。模型预测结果如图8 所示。
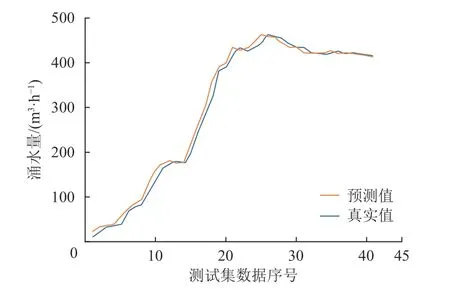
图8 亭南煤矿401 工作面涌水量预测结果Fig.8 Predicted mine water inflow for the mining face 401 of the Tingnan Coal Mine
模型的EMA为9.5 m3/h、ERMS为1.9 m3/h、EMAP为8%。由模型的预测结果和评估指标可得:预测结果与实际观测值的偏差相对较小,预测的准确性相对较高,说明模型在预测涌水量方面具有较好的性能。
需要注意的是,如果新数据与训练数据有较大的特性差异,模型的性能可能会下降。在这种情况下,需复现整体实验,根据矿井或工作面数据特性,确定相关性良好的若干影响因素,重新训练模型、调整模型参数或者微调模型,以适应新数据的特点。
5 结论
a.钻孔水位、微震能量与工作面涌水量数据之间存在强相关性,因此,可以通过分析钻孔水位、微震能量数据预测涌水量变化规律。
b.将水位、微震能量数据作为工作面涌水量预测特征输入到多因素涌水量预测模型中,涌水量预测的偶然性得到抑制,相比单因素预测模型,预测结果更加准确、可靠、稳定。
c.SSA-CG-Attention 模型可用于涌水量多因素预测,提取时序特征,兼顾数据局部特征,将注意力集中在相关的输入元素上,尽可能多地学习输入数据特征,同时通过麻雀搜索算法优化模型参数,以最少的迭代次数快速寻找网络参数,避免局部最优解的缺陷,提升了预测准确性。
d.该模型仅考虑了水位和微震能量数据,下一步将继续获取其他相关影响因素数据,如多组水位、降水量等,对多因素预测模型进行深入探究。
符号注释:
ai为输入向量的权重;A+=AT(AAT)-1,A为每个元素为1 或-1 的(1×d)维矩阵;D为指标方差和;fi为麻雀个体的适应度值;fg、fw分别为全局最佳和最差适应度值;h1,h2,···,hi为对应于输入序列的隐藏层状态;h'为最终的特征向量;ht、ht-1分别为当前和上一时刻隐藏层输出;i为第i个麻雀;k为池化窗口大小;K、β均为随机数,取[-1,1];L为1×d的全1 矩阵;m为模型评价指标个数;n为样本数量;N为迭代次数;Nmax为最大迭代次数;P为填充大小;Q为服从正态分布的随机数;rt为t时刻重置门输出;R2为警戒值;s为池化窗口的步长;S为安全阈值,S∈[0.5,1];W为各特征值的权重向量;xc为输入数组x的大小;x1,x2,···,xi为输入序列;为第i个麻雀在第j维的第N+1 次迭代,其他同位置信息;为发现者第N+1 次迭代占据的最佳位置;xt为t时刻输入变量;为当前最差位置;为当前全局最优位置;为每次迭代指标的平均值;X为提取出的特征向量;yc为输出数组y的大小;y为样本实际值;yi为样本预测值;Y为最终的特征输出向量;zt为t时刻更新门输出;∂为属于[0,1]的随机数;ε为常数;⊗为向量间的逐元素相乘;⊕为向量间的逐元素相加;δ为sigmoid 函数,可将数据变为[0,1];tanh 为双曲正切函数,可将数据变为[-1,1]。
