武汉城市圈生态网络鲁棒性模拟及稳定性分析

黄悦, 李红波, 欧国良

武汉城市圈生态网络鲁棒性模拟及稳定性分析

黄悦1,2, 李红波1,*, 欧国良3

1. 华中农业大学公共管理学院, 武汉 430070 2. 武汉永业赛博能规划勘测有限公司, 武汉 430061 3. 深圳职业技术学院建筑与环境工程学院, 深圳 518055

生态网络在不同破坏程度或干扰强度下呈现出不同的鲁棒性, 势必造成区域生态系统的稳定性风险。基于武汉城市圈生态网络的构建与识别, 建立节点和廊道的重要性评价体系, 运用鲁棒模型模拟随机干扰情景下的鲁棒性变化评价生态网络的稳定性特征。结果表明: 基于复杂网络理论对武汉城市圈生态网络进行拓扑网络提取, 共生成117个节点和189条连接线, 重要性等级较高的节点占23.9%, 主要分布在研究区中北部区域, 重要性较低的节点占节点总数的51.3%, 主要分布在研究区的西北和东南地区; 采用重力模型判别生态廊道重要性, 得到17条重要廊道, 28条一般廊道, 重要廊道对生态网络的连通性和稳定性具有极大影响; 节点数量和重要度对网络的稳定性具有显著影响, 当节点失效率低于50%时, 生态网络稳定性变化较小, 整体处于较高的稳定性; 当节点失效率在50%—85%时, 生态网络极其不稳定; 当节点失效比率达到85%时, 生态网络开始瘫痪; 依据生态节点和廊道的重要性以及模拟结果, 分别提出生态节点保护和廊道建设的差异化管理策略。

生态网络; 稳定性; 鲁棒性; 武汉城市圈

0 前言

我国目前已进入以都市圈和城市群为主要动力的发展阶段, 产业的聚集, 就业机会的增加, 资源的分配, 尤其是土地资源利用变化, 直接扰动了区域生态系统的服务能力[1]。在生态文明建设战略背景下, 都市圈规划的实施和建设必然摒弃以往几十年来生态环境为代价的发展模式, 尽管地方政府已采取行动, 不断协调经济发展与生态保护的关系, 但这种模式发展惯性短期难以完全消除, 在时间和空间尺度上, 都市圈内生态系统扰动此起彼伏在所难免。城市圈空间点-轴式扩张和圈层结构发展、追求短期效益、城市内部生态污染、生物多样性减少等问题, 对城市圈生态系统的持续稳定性造成一定的显著风险[2-3]。生态网络作为分析生态系统结构和功能变化规律行之有效的方法[4-6], 将各个生态要素空间连接成复杂网络系统, 其稳定性对生态系统结构的稳定性、功能的复杂性和保护生物多样性具有关键作用[7]。不同地区生态网络具有相应的地域特征, 网络的构建和稳定性分析是空间规划及生态建设的重要依据, 因此, 研究生态网络结构及其稳定性对生态系统保护与治理具有重要意义。

生态网络在不同破坏程度和干扰强度下呈现出不同的稳定性, 而生态网络的鲁棒性用以表征生态系统对特性或系统参数扰动的不敏感性, 即当某个系统遭遇外部冲击或内部结构变化对其造成影响时, 系统的变化趋势以及保持原有系统功能的能力, 是衡量整体网络运行效率的重要指标[8-9]。复杂网络的鲁棒性分析通常采用节点效率大小进行排序, 它可以通过对控制变量来测试网络的稳定性与否, 来处理网络结构优化、风险管控等问题[10-11]。目前, 有关网络稳定性领域的研究主要集中在人工智能、通信工程、计算机科学等领域, 通过干扰抑制或信息间隙决策理论进行网络鲁棒性优化[12-15]解决耦合层之间的级联障碍获得整个网络的最佳鲁棒流量分配规则[16]。许多学者对生态网络构建的理论和技术进行了广泛探索, 将其他学科的理论方法融入到生态网络的研究上, 通过阻力因子选取、评价指标体系构建、地理信息技术应用等方法来研究生态网络。对于生态网络的已有研究成果虽然比较丰富, 然而现有研究局限于生态网络的构建与优化[17], 从不同尺度层面分析区域生态网络[18], 并兼顾网络特征识别与生态服务水平提升[19], 缺乏生态网络结构与组织层面的网络稳定性分析。有研究尝试利用鲁棒性来分析生态网络的空间结构和内部功能, 例如: 采用不同增边策略分析荒漠绿洲区域生态网络优化前后鲁棒性的变化特征[20]; 基于复杂网络评价方法, 分析复杂层级网络的拓扑结构与空间鲁棒性对生态网络结构、功能稳定性的影响[21]。鲁棒性已成为网络控制理论中的一个重要研究领域, 在生态系统稳定性研究上的重要性初显。

本研究以武汉城市圈为研究区, 采用最小累积阻力模型构建生态网络并提取拓扑网络结构, 通过Pajek软件计算网络的点度、紧密度、中介度、和特征向量指数, 构建节点综合重要度模型, 评定节点级别; 运用重力模型判别生态源地之间潜在生态廊道的相互作用强度, 识别重要生态廊道; 运用鲁棒性模型分析武汉城市圈网络稳定性程度, 通过网络结构破坏情景模拟, 分析网络的连通鲁棒性和脆弱鲁棒性的变化, 以此来判断武汉城市圈生态网络稳定性状况。以期为区域生物多样性保护、维持生态系统稳定和生态保护规划及相关工作的开展提供参考依据。

1 研究地区与研究方法

1.1 研究区概况

武汉城市圈(29°05'—31°51' N, 112°30'—116°07' E)位于湖北省东部、长江中游, 指以武汉市为中心, 包括武汉及其周边100 km范围内的黄石、黄冈、鄂州、孝感、咸宁、仙桃、潜江、天门9个城市所组成的城市群(图1)。武汉城市圈占湖北省面积的三分之一, 却贡献了全省60%的GDP, 是湖北省经济发展的核心区域, 也是中部崛起的重要战略支点。武汉城市圈从2007年开始着力推进“资源节约型和环境友好型”社会试点区建设, 明确环境保护与资源节约的发展机制, 推动跨区域经济建设与生态保护的可持续发展。2018年, 城市圈总面积约5.8万km2, 常住人口约3800万, 形成了优势互补、资源共享的经济发展格局。随着经济建设与城镇用地的扩张, 快速城镇化与生态环境的矛盾日益突出, 生态系统服务功能逐渐弱化, 因此, 研究武汉城市圈生态网络的稳定性状况显得极其重要。

图1 研究区位置示意图

Figure 1 Sketch map of the location of the study area.

1.2 数据来源与处理

本研究数据主要包括2018年的Landsat TM/ OLI遥感影像数据、数字高程模型(DEM)数据、道路矢量数据。遥感影像数据和DEM数据来源于地理空间数据云(http: //www.gscloud.cn/), 空间分辨率为30 m。2019年的道路数据来源于OpenStreetMap网站(https://www.openstreetmap.org/), 主要采用高速路、国道、省道和县道4类道路。利用RS软件采用面向对象的分类方法对遥感影像数据进行解译分类, 参考《土地利用现状分类》标准(GB/T21010— 2017)[22], 并根据实际情况进行重新分类, 得到6类土地利用分类图(图2), 解译精度为83.7%, 满足本研究要求。

1.3 研究方法

1.3.1 生态网络构建

以林地、草地和水域作为前景数据, 采用形态学空间格局方法(MSPA)[23]识别和提取出对物种迁移和能量交换具有重要作用的核心区景观。选用景观连通性指数对面积大于100 km2的核心区斑块进行景观连接度评价, 斑块重要性指数越高, 说明重要性越大, 提取出斑块重要性指数大于1.2的10个核心区斑块作为研究的生态源地。阻力面的构建需要综合考虑自然和人为等因素, 考虑数据的可获取性和研究区的实际情况, 参考相关文献[24-26], 从自然地理和人为活动等方面选取景观类型、高程、坡度、距道路距离、距建设用地距离5个指标来构建综合阻力面, 使用GIS软件中的成本距离模块中的最小成本路径工具, 根据生态源地和阻力面, 生成目标源地到其他源地斑块的最小累积阻力路径, 从而获得了由生态源地和生态廊道组成的武汉城市圈生态网络(图3)。

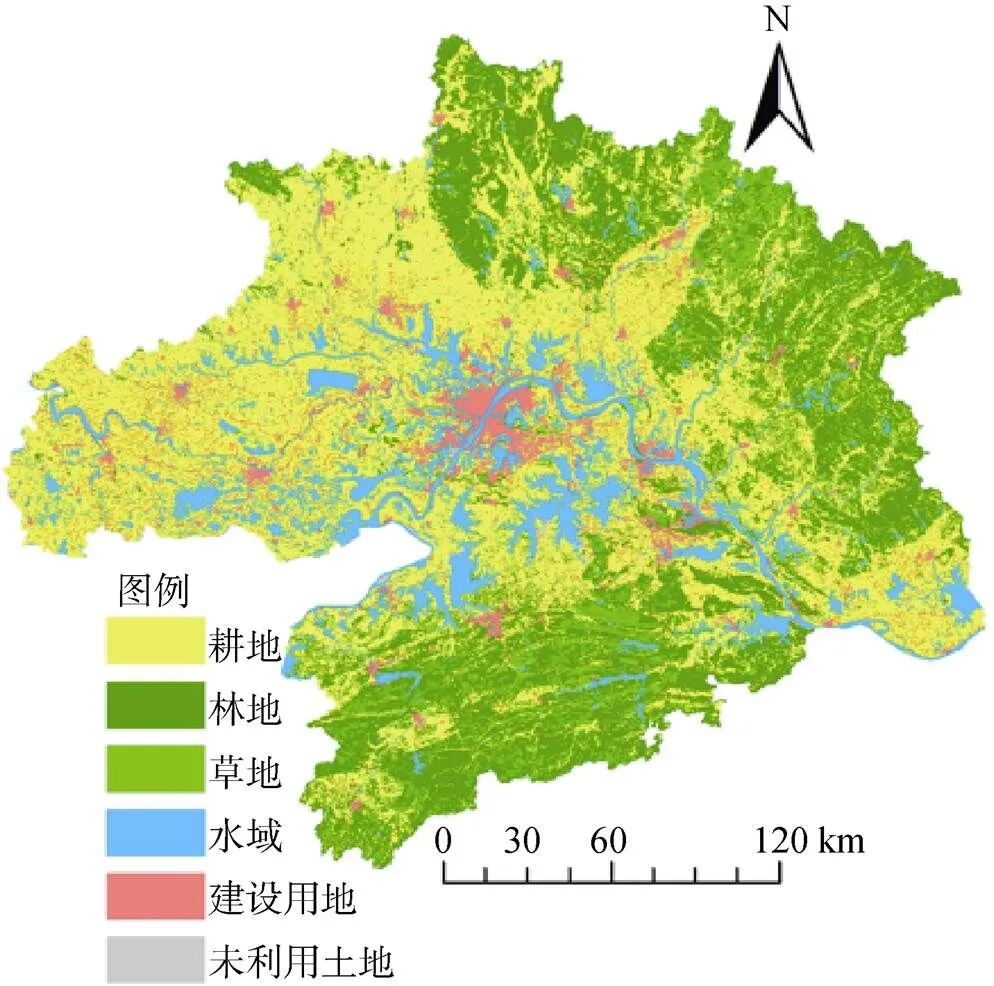
图2 土地利用类型图

Figure 2 Land use classification.

1.3.2 网络节点综合重要度评价

节点与源地分布在生态网络范围内, 对维持生态网络的稳定性具有重要影响。生态斑块与生态节点在网络中的组织结构和发挥的具体生态功能对其重要性具有极大影响。利用Pajek软件[27-29]对构建的生态网络进行拓扑结构提取, 生成武汉城市圈的拓扑网络图。结合研究区生态网络的自身特性, 通过计算网络中节点的点度、紧密度、中介度和特征向量度, 构建节点综合重要度评价模型, 对网络节点进行评估, 得到网络中各要素的综合重要程度[30]。点度表示与某一节点所相连的廊道数量, 数值越大表示该节点在网络中可调度的物质资源越多, 能量流和生态流在该节点进行传输的可能性越大。紧密度指某节点与其他任一节点的最小距离之和, 其值越大说明节点之间的功能联系越强。中介度表示其他节点两两间的所有最小距离路径中有包含该节点的比例。特征向量度是指在经过一定的变换后方向仍不发生改变的向量。若某节点与联系节点位于网络中心位置时, 则该节点的特征向量度最大[31]。节点重要性的计算公式如下:

Q=θD+ηC+γB+δH(1)

式中:Q表示节点的综合重要度值;D、C、B、H分别表示某生态节点的点度、紧密度、中介度和特征向量度;、、、、分别表示相应的权重值。

1.3.3 生态廊道重要性评价

生态廊道的有效性和重要性可以根据生态源地斑块之间的相互作用强度来定量分析[32]。生态源地的面积和生态廊道的宽度对物种的迁移环境具有很大影响, 廊道宽度是基于标准化后的累计成本距离所提取, 廊道越宽其阻力值就越小。宽度较大的生态廊道更便于物种迁徙和能量流通, 有利于促进生态系统的稳定。重力模型能够对空间中各个研究对象彼此之间的作用强度和依存关系进行定量描述, 一般用来分析在地理空间中研究对象的相互联系。基于重力模型, 生成生态源地斑块之间的相互作用矩阵, 根据各个斑块之间的相互作用强度, 从而识别和提取重要生态廊道。重力模型计算公式如下:

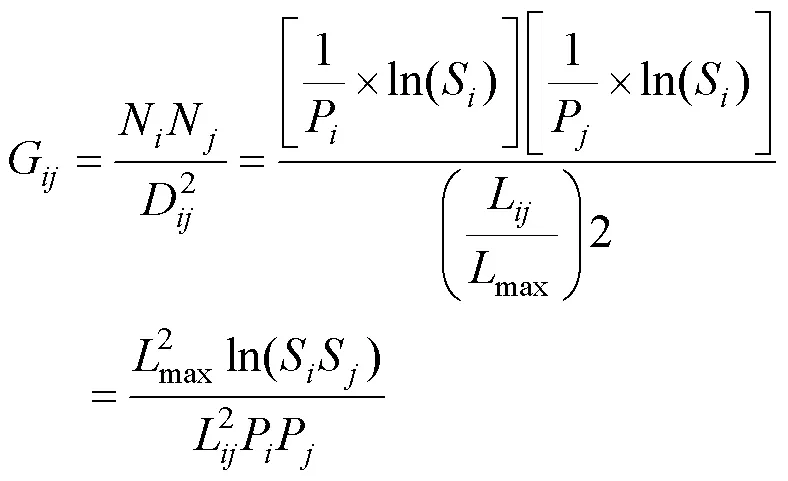
式中:G是源地斑块与之间的相互作用力;N和N为斑块和的权重值;D是两斑块之间标准化的廊道阻力值;P为斑块的阻力值;P为斑块的阻力值;S和S为两斑块的面积;L表示斑块到斑块之间的平均标准化廊道累积阻力值;max指网络中所有廊道阻力的最大值。

1.3.4 生态网络稳定性分析

生态系统在面临特定干扰时依然维持生存延续功能的特性以及系统结构的稳定性程度可用鲁棒性刻度[33]。根据复杂网络结构理论, 通常采用连通鲁棒性和脆弱鲁棒性指标[34-37]进行网络稳定性的评价。本研究采取随机去掉生态网络中节点的“随机攻击”模式, 据此探究对应情景下生态网络稳定性的动态变化情况。为保证随机情景设置的客观性, 利用“在线随机数生成器工具”, 随机生成117个整数, 对网络中的117个节点进行随机排序。按照随机数的排列顺序, 将数字对应的节点进行攻击, 并计算出每次攻击后的鲁棒性。

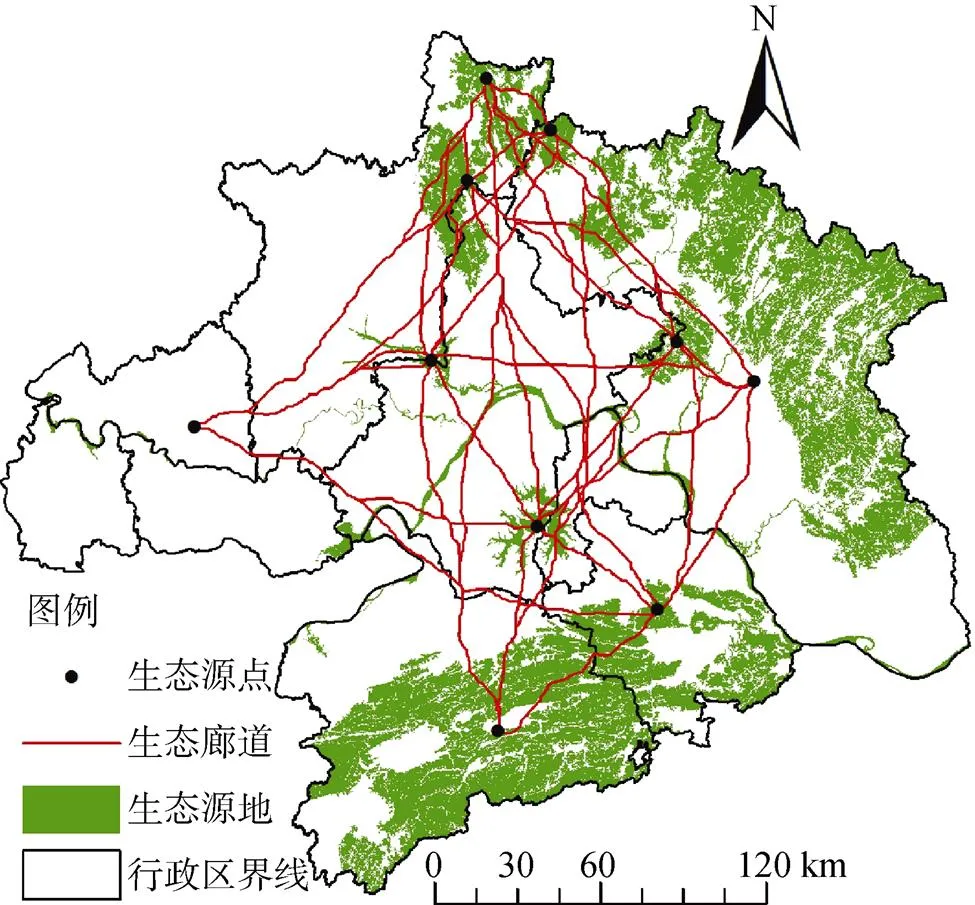
图3 武汉城市圈生态网络

Figure 3 Ecological network in Wuhan metropolitan area

1)连通鲁棒性。连通鲁棒性表示在外力干扰破坏下造成网络要素的损失后, 系统为了维护网络中各要素的稳定连通以及物质和能量传输的能力。在网络系统受到攻击时, 连通性越大, 表明网络的随机应对能力越强。计算公式如下:

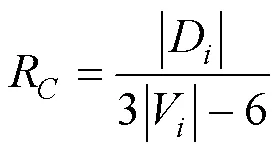
式中:c表示连通鲁棒性;为生态网络节点(=1、2、3…); |D|表示删除节点时生态网络中边的数目; |V|表示删除节点时网络中的节点数目。

2)脆弱鲁棒性。在复杂网络系统中, 常用脆弱鲁棒性指标来反映网络在遭受外界攻击时能量的运行效率。物质信息流的运行能力一般用全局效率表示[38-40], 基于脆弱鲁棒性与全局效率表达的相似性, 因而采用全局效率计算公式来表征网络的脆弱鲁棒性值, 值越大表明系统运行得越高效, 前提是假设节点两两之间的能量均从最短路径进行流动。计算公式如下:

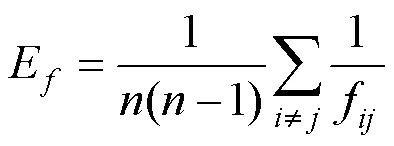
式中:E表示生态网络的脆弱性鲁棒值;表示网络中的节点个数;和表示从属于同一网络中的不相同的节点;f指两个节点之间的最短距离。

2 结果与分析

2.1 节点综合重要度评价

基于复杂网络理论, 在不考虑源地面积和信息流传播量大小的前提下, 假设源地、节点之间的物质能量流动和信息传播的方向均为双向流动, 从最小累积阻力模型构建的生态网络提取拓扑网络, 将生态网络简化成由节点和线组成的无方向且无加权边的拓扑网络结构。利用Pajek软件将生态源地(大型生态斑块)、生态节点(生态源地中心点和廊道交点)、生态廊道(如绿道、河渠、湖泊)进行拓扑提取, 生成117个节点和189条连接线(图4)。将.net文件导入到Pajek中, 使用Draw命令生成拓扑图像(图5)。

图4 研究区网络结构

Figure 4 Network structure of the study area.

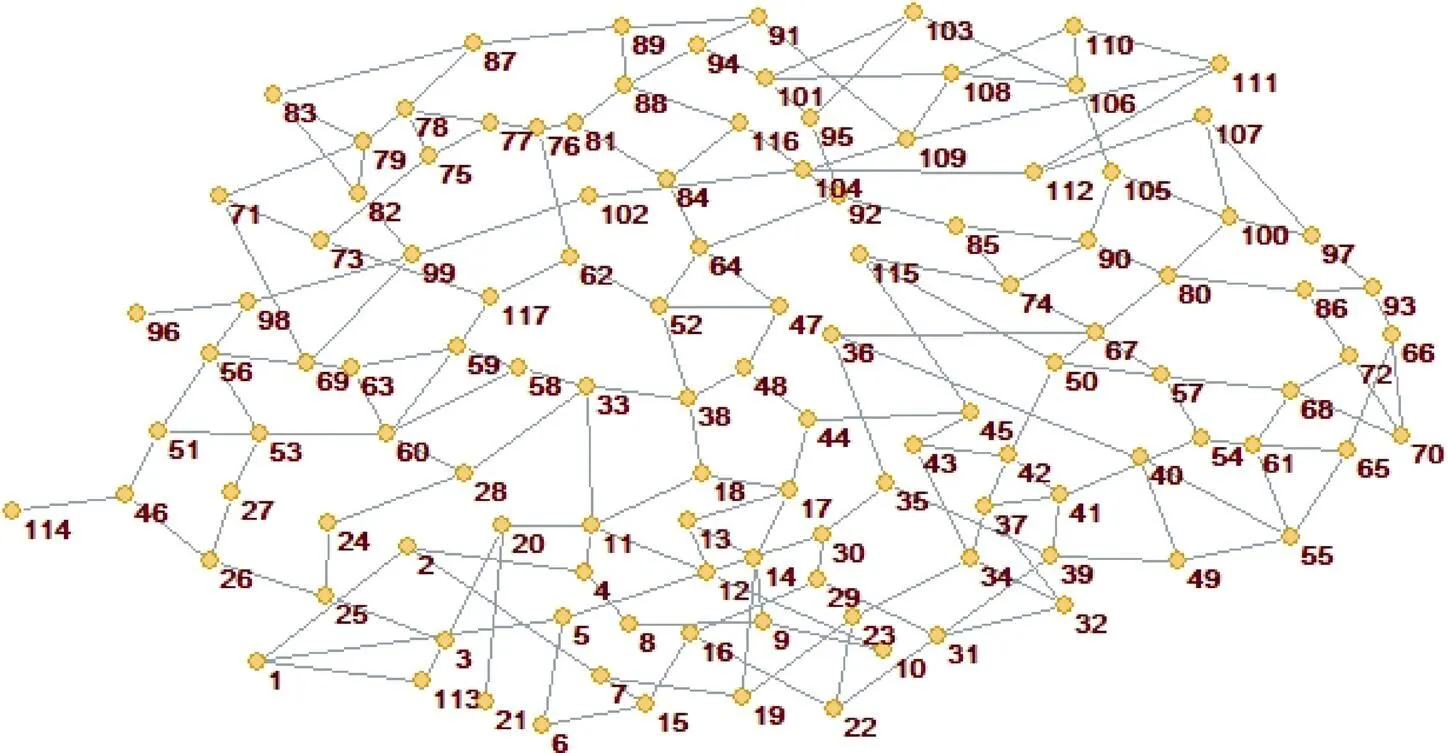
图5 拓扑网络结构

Figure 5 Topological network structure.

基于Pajek软件, 通过输入一系列的计算命令来运算网络中生态节点的点度、紧密度、中介度和特征向量度。将计算结果进行Z-core无量纲标准化处理, 再采用层次分析法确定指标权重值θ、η、γ、δ(表1), 根据公式(1)计算节点综合重要性, 并采用聚类分析法将节点重要度划分为高、较高、一般、较低、低5个等级。

由表2和图6可以看出, 节点数量基本呈正态分布, 其中, 重要性等级高和较高的节点仅占总节点数量的23.9%, 且主要分布在研究区中北部, 林地景观面积广阔, 该区域生态源地面积较大, 生态廊道密集, 生态节点分布较多, 发挥着生态网络中的能量信息传播的重要功能。重要性低和较低的节点占节点总数的51.3%, 主要分布在研究区的西北和东南地区, 该区域生态斑块比较分散, 生态廊道冗长, 连通性较差, 物种迁徙和能量信息流动易受阻。东部地区节点数量较少, 重要性低的节点居多, 零星分布有重要性较高的节点, 该区域的生态廊道为南北延伸的狭长通道, 节点连接的廊道数量较少, 景观连通性相应较差。重要性高或较高的节点对维护生态网络稳定具有关键作用, 因此, 针对这类节点应提出具有相对应的保护建议, 提高区域生态网络的稳定性和生态系统的可持续发展。

2.2 生态廊道重要性

完整生态网络的主要组成要素为生态节点和生态廊道, 节点和廊道的效率都会对生态网络的稳定性产生重要影响。因此, 在保障生态系统安全和维持生态网络稳定时, 不仅要关注生态网络中的关键节点, 还要重点把握生态网络中廊道的重要性程度。生态源与目标源之间的相互作用强度是衡量源地之间生态廊道有效性和重要性的主要指标之一。通常认为, 生境质量越好的斑块越能减少物种迁徙, 降低生态流流动交换时的阻力, 增加物质能量信息传输中生物的幸存比率[41]。因此, 生态网络的构建与优化都需要对潜在生态网络进行修正和优化, 为完善生态网络整体结构完整和功能稳定以及构建合理科学的生态空间提供重要依据。基于重力模型, 建立了10个生态源地相互间的作用力矩阵(表3)。在参考已有研究的基础上[42], 考虑到利于武汉城市圈生态环境差异化管理, 根据生态源地的大小, 并依据作用力数值大小对廊道进行重要性分级, 大于100的作为重要廊道, 等于或小于100的当作一般廊道。

武汉城市圈基于重力模型识别的重要廊道有17条, 主要分布在研究区的北部和东南部, 主要连接北部的大别山林区和南部的九宫山等山群(图7)。这些重要生态廊道是物种能量与信息交换的主要通道, 也是阻力最小的便捷路径。一般廊道数量较多, 分布广泛, 经过研究区的大部分市县, 距离人类聚集活动区域较近, 受人类活动干扰频繁, 且生态斑块面积较小, 不适宜大范围的物种迁移活动。

表1 节点综合重要度评价指标权重

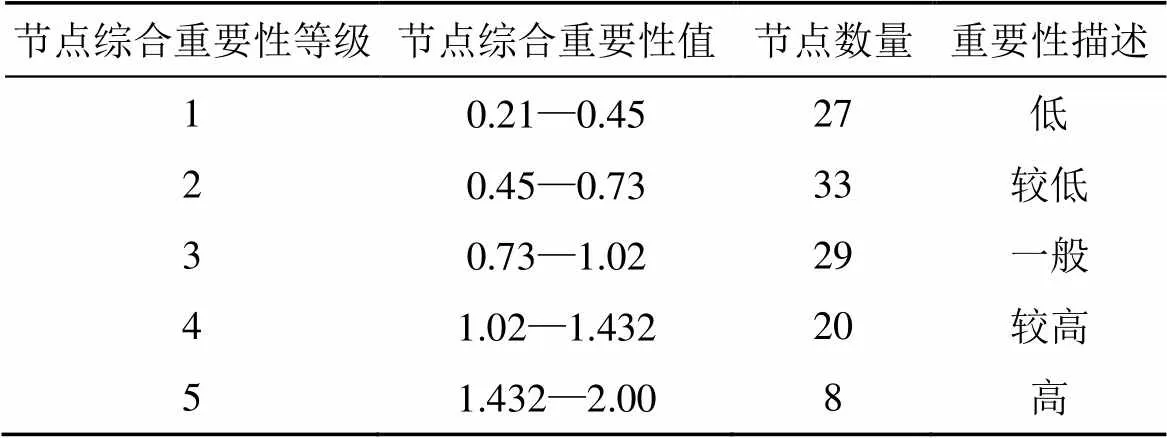
表2 节点综合重要度评价结果

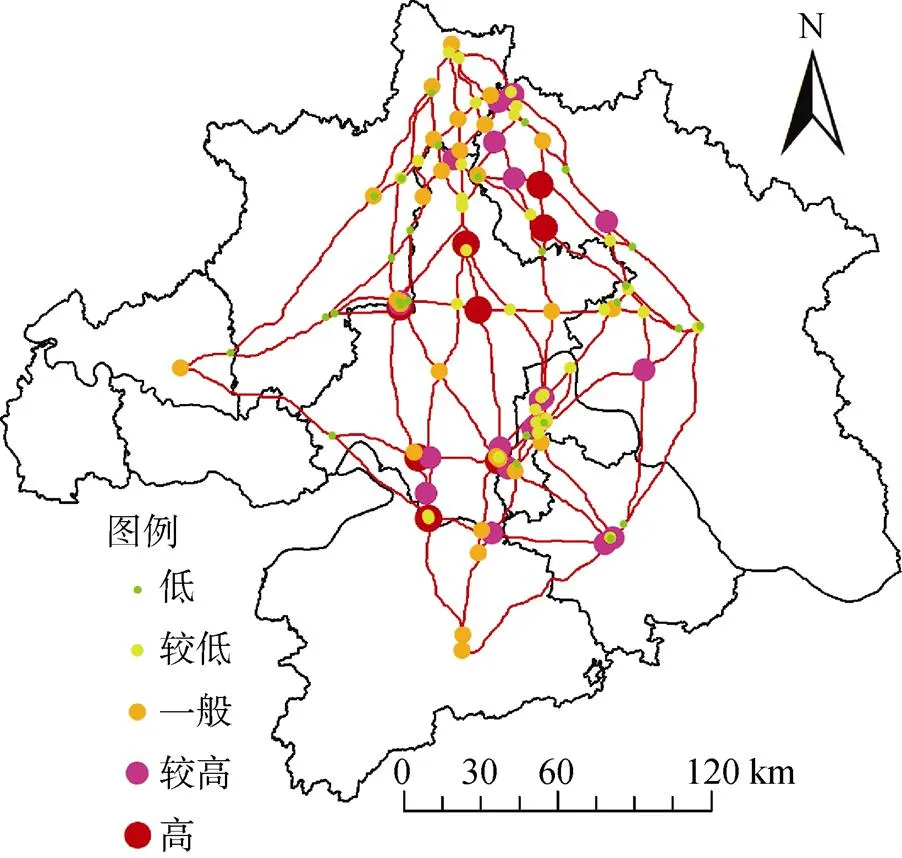
图6 节点综合重要度的空间分布

Figure 6 Spatial distribution of node comprehensive importance.

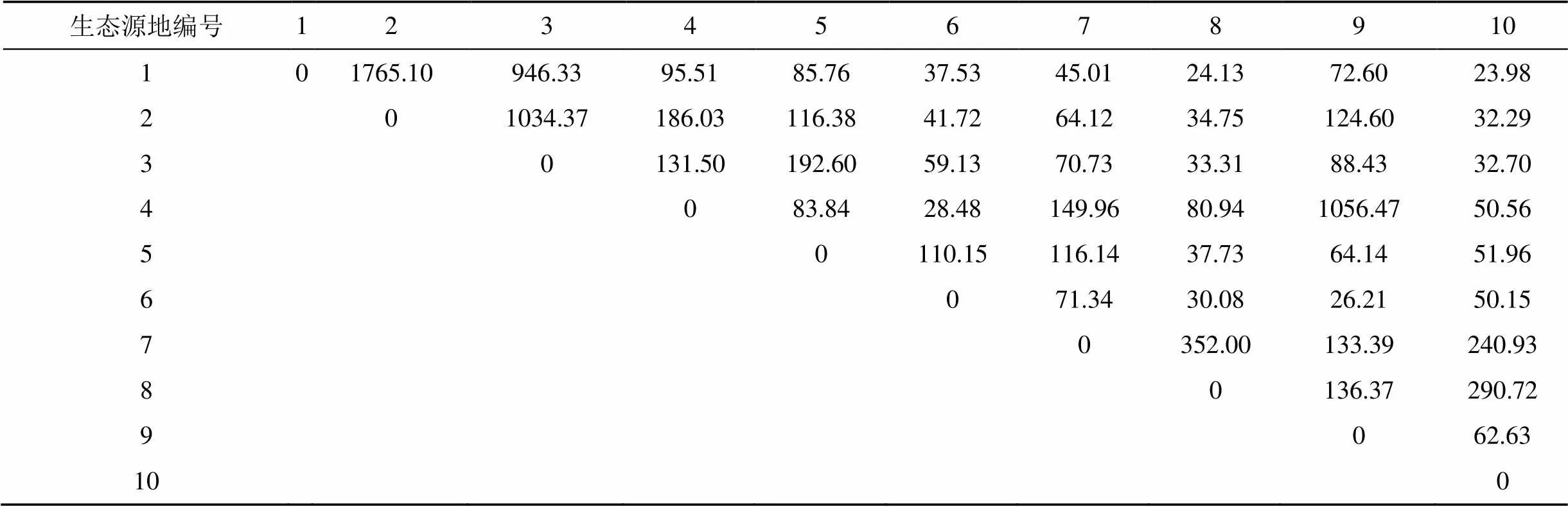
表3 基于重力模型的生态源地间相互作用矩阵

图7 生态廊道重要性分级

Figure 7 Ecological corridor importance classification.

2.3 鲁棒性模拟

运用鲁棒模型分析生态网络的连通鲁棒性和脆弱鲁棒性通常需要先假设某个特定的场景, 即某种情景假设[43]。武汉城市圈尚处于都市圈培育阶段,城镇化加速、土地利用及覆被过去和将来变化依然显著, 而且每隔3～5年发生一次严重的洪涝灾害, 生态网络节点存在随机破坏的潜在风险。因此, 本研究选择“随机攻击”破坏模式, 有序地删除网络中的节点, 模拟随机破坏情景, 计算生态网络的两种鲁棒性。

删除的节点数量对网络的稳定性具有极大影响。由图8可以看出, 在随机破坏情景模拟下, 网络的连通鲁棒性和脆弱鲁棒性与节点删除数量密切相关, 且均呈下降趋势。连通鲁棒性的起始值为0.55, 脆弱鲁棒性的起始值为0.26, 鲁棒值越大说明网络稳定性越强。当删除节点数量小于57%时, 连通鲁棒性起伏较小, 网络暂时处于相对稳定状态, 当删除节点数量达到57%时, 连通鲁棒性开始出现明显下降, 下降后呈平缓下降趋势, 当删除节点数量达到85%时, 连通鲁棒性值开始发生剧烈下降, 说明此时的生态网络遭到较大程度的破坏, 网络中剩下的节点不具备景观连通功能, 整个网络开始趋于瘫痪状态。当删除节点数量仅为8.5%时, 脆弱鲁棒性值开始呈下降趋势, 这与此时删除节点的重要程度有关, 与删除节点有关联的节点数量较多且处于网络的中部区域; 当删除节点数量达到47%和68%时, 脆弱鲁棒性出现平缓下降趋势, 当删除节点数量达到88%时, 脆弱鲁棒性值急剧下降, 网络结构破坏严重, 整体网络开始处于瘫痪状态。

图8 连通鲁棒性和脆弱鲁棒性的变化

Figure 8 Change of connectivity and fragile robustness.

连通鲁棒性和脆弱鲁棒性整体变化趋势基本一致, 可以判定, 85%左右的节点失效临界值是武汉城市圈生态网络维护整体结构功能的关键, 也是保持网络稳定性和连通性的重要临界值, 当节点失效比率低于85%时, 连通鲁棒性虽有下降但趋势缓慢, 脆弱鲁棒性有小幅上升但整体呈缓慢下降趋势; 当节点失效比高于85%时, 连通鲁棒性和脆弱鲁棒性均呈急剧下降趋势, 生态网络开始处于瘫痪状态。由此可知, 节点失效比率是影响生态网络结构稳定的关键指标, 网络整体结构的稳定性可以由一定区间内的节点失效率来反映, 也可用来量化整体网络空间的复杂性。

节点数量对整体生态网络的复杂性和稳定性具有重要影响, 也对丰富物种类别程度和生态功能多样性具有关键作用。比较两种鲁棒性曲线的变化趋势, 可以发现脆弱鲁棒性的波动起伏比连通鲁棒性要高, 说明节点数量对网络运行效率的影响高于对网络连通性的影响, 从而影响到整个网络的稳定性。总体看, 在节点失效率较低时, 武汉城市圈的生态网络处于比较稳定的状态, 说明在自然状态下生态系统能够进行自我调节, 物种信息流动阻力仍较小, 对生物多样性的影响变化不大。只有当节点失效率大于85%时, 这种自我调节能力开始急剧下降直至完全丧失。节点失效率过大时, 生态网络内的节点破坏程度大于生态系统的自我恢复能力, 关键节点被破坏, 原有的运输通道被割断, 物质信息流动严重受阻, 从而导致生态网络的不稳定性加强, 不利于生态系统的持续健康发展。重要程度高的节点对维持生态网络的稳定性具有关键作用, 删除节点的综合重要度越高, 对网络稳定性的影响越大, 越容易造成网络连通鲁棒性和脆弱鲁棒性发生剧烈变化, 因此, 重要度高的节点是保障网络连通性和能量信息传递的关键, 对维持生态空间网络稳定性起着重要作用。

3 生态网络保护管理策略

3.1 生态节点保护策略

节点是保持网络稳定性和连通性的关键, 其在网络中的贡献程度、数量、相互作用力是维持网络结构稳定性和复杂性的重要因素。为实现节点在生态网络中的重要作用, 依据节点综合重要度评价结果, 制定重点保护、一般保护、广泛保护3种节点保护策略。

(1)重点保护策略。对重要度较高的节点进行保护来维持生态网络稳定性。该类节点数量较少, 相对集中在鄂州市的湖泊区域和黄冈市的大别山区, 节点所对应土地利用类型多为林地, 对整体网络空间的稳定性产生关键影响, 因此, 在生态网络空间遭受到一定干扰破坏时, 重点保护这类节点能保证生态网络的基本功能, 但处于该保护策略下的生态网络处于较敏感的状态, 且稳定性较低, 若生态网络继续被破坏导致节点继续丧失, 生态网络将很快完全瘫痪。

(2)一般保护策略。对节点综合重要度一般以上的节点进行保护, 保护节点数量高于重要保护策略, 可将总节点数量的48%纳入该保护策略中, 主要为武汉城市圈的北部林地, 虽然能保护的节点数不到总节点数量的一半, 但能够保证生态网络的相对稳定。

(3)广泛保护策略。对节点重要性等级为二级以上的节点进行保护, 保护节点数占总节点数量的76%, 主要集中于研究区的北部和南部区域。由于被保护的节点数量多, 景观类型丰富, 生态网络能够在较长时间范围内维持自身的稳定性, 其生态结构和功能不会因外界干扰而发生较大波动。

3.2 廊道重要性保护策略

生态廊道是连接生态源地的重要生态流通道, 由于不同廊道的功能和效用存在差异, 其在网络中的建设能力和所发挥的作用也有差别。根据廊道重要性的判别结果, 针对生态廊道重要性差异, 制定不同的廊道保护策略, 从而提升整个生态网络的完整性和稳定性。

(1)重要生态廊道保护建设策略。重要生态廊道相对集中于研究区的北部和东南部区域, 连接的是具有关键生态功能的生态源地, 是国家森林公园、自然保护区和水源保护区的重要连接通道, 是阻力较小的流通路径。重要廊道的主要土地利用类型为林地, 应强化该类生态廊道的保护建设, 促进核心生态源地之间的物质交换和信息流通。

(2)一般生态廊道保护建设策略。一般生态廊道广泛分布在研究区的中部和西部区域, 连接的斑块主要是面积较小且较为分散的生态源地, 源地间的相互作用力较小或距离较长, 该类生态廊道阻力较大, 对源间生态物质流的流通有一定影响, 且研究区重要廊道数量多于一般廊道。因此, 对一般廊道进行缓冲区保护建设, 能更好地提高生态网络整体的安全性和稳定性。

4 讨论

生态网络是有效分析生态系统功能和组织结构的重要手段, 网络的结构和稳定性对于生态建设具有重要意义。在城市大规模扩张或城市圈高速发展阶段, 原有的生态环境遭到破坏, 生态系统稳定性面临挑战。鲁棒性反映了生态系统在遭受外部环境冲击或内部结构变化时的敏感性, 可以表征建设用地扩张、生态空间压缩时生态网络的稳定性变化, 把握当前的生态建设状况, 从而对区域生态环境可持续发展提供一定指导。一方面, 武汉城市圈每3—5年发生一次严重的洪涝灾害, 对生态网络具有潜在的扰动风险, 为维持生态系统稳定性, 可通过灾前的工程建设和灾后的生态恢复, 重建生态网络。另一方面, 武汉城市圈处于都市圈的培育阶段, 建设用地作为武汉城市圈迅速发展的表现, 其面积的不断扩张势必对生态系统的持续稳定发展造成影响, 引发环境污染、生物多样性减少等生态环境问题。因此, 在土地利用覆被未来变化的不确定性下, 模拟生态网络在随机破坏情景下的鲁棒性变化, 对节点和廊道进行差异化保护, 对于提升生态网络的整体稳定性具有重要意义。

关于生态网络稳定性的分析方法, 国内目前相关的研究内容较少。在参考借鉴电气工程、通信工程等交叉学科的网络鲁棒性分析思路与方法的基础上, 本研究构建生态网络鲁棒性模型, 分析武汉城市圈生态网络稳定性。受限于篇幅, 仅考虑了随机攻击的情景模式下的连通鲁棒性和脆弱鲁棒性, 并且在分析节点失效情况时, 仅考虑了节点失效时的比率, 未能考虑节点失效之后可能恢复的概率。在遥感数据和大数据结合的背景下, 编程语言和拓扑网络方法的应用使生态网络稳定性研究更具科学性, 未来在生态网络稳定性和复杂性领域的研究还须进一步深入。

5 结论

基于节点综合重要性评价、廊道重要性评价以及鲁棒性分析, 对武汉城市圈生态网络进行拓扑网络提取, 分析节点的综合重要程度, 识别出不同重要性等级的生态廊道, 模拟遭受破坏随机情景下生态网络的连通鲁棒性和脆弱鲁棒性对整体生态网络稳定性的影响。评价武汉城市圈的生态网络的稳定性, 提出了生态网络保护管理策略的设想, 对未来区域生态网络保护管理策略的制定具有一定指导意义, 可为城市圈国土空间规划编制和自然保护区划定提供一定参考。结论如下:

(1)武汉城市圈的拓扑网络共有117个节点和189条边, 根据节点综合重要度评价结果, 重要性等级较高的节点占23.9%, 主要分布在研究区中北部林地区域, 是物种迁移和能量交换的重要功能性区域; 重要性较低的节点占节点总数的51.3%, 主要分布在研究区的西北和东南地区, 该区域生态斑块比较分散, 离人类活动区域较近, 受人类活动影响较大, 物种迁徙和能量信息流动易受阻。

(2)基于重力模型, 得到武汉城市圈重要生态廊道有17条, 一般生态廊道有28条。重要廊道主要分布在研究区的北部和东南部林地区域, 是生物信息流和能量流交换的重要通道, 对维持网络的稳定性具有重要作用。一般廊道数量多, 且分布较为分散, 连接的节点距离较远, 易发生断裂, 不利于大规模的物种迁移活动。

(3)生态网络稳定性与节点的重要度和数量密切相关, 重要度高的节点对于维持生态网络的稳定性具有重要作用, 节点数量也在一定程度上影响网络结构的稳定性。武汉城市圈的连通鲁棒性起始值为0.55, 脆弱鲁棒性起始值为0.26, 随着节点数量的减少, 两种鲁棒性均呈下降趋势; 85%的节点失效率是维持网络稳定性和连通性的重要临界值, 说明要维持网络的稳定性, 必须保证一定数量的重要度高的节点, 这也是保护武汉城市圈整体生态网络结构功能的关键。

[1] 陈万旭, 刘志玲, 李江风, 等. 长江中游城市群生态系统服务和城镇化之间的空间关系研究[J]. 生态学报, 2020, 40(15): 5137–5150.

[2] 张军泽, 王帅, 赵文武, 等. 可持续发展目标关系研究进展[J].生态学报, 2019, 39(22): 8327–8337.

[3] 高莉洁, 崔胜辉, 郭青海, 等. 关于可持续城市研究的认识[J].地理科学进展, 2010, 29(10): 1209–1216.

[4] 李中才, 徐俊艳, 吴昌友, 等. 生态网络分析方法研巧综述[J]. 生态学报, 2011, 31(18): 5396–5405.

[5] SILVIA P, PERE S, LUCA S. Landscape and the city: Agro-forest systems, land fragmentation and the ecological network in Rome, Italy[J]. Urban Forestry & Urban Greening, 2019, 41(5): 230–237.

[6] LONG C, VRIES S D, VENEMA K. Polysaccharide source altered ecological network, functional profile, and short-chain fatty acid production in a porcine gut microbiota[J]. Beneficial Microbes, 2020, 11(6): 591–610.

[7] LV Zhiyuan, YANG Jun, BEN W, et al. Prioritizing Green Spaces for Biodiversity Conservation in Beijing Based on Habitat Network Connectivity[J]. Sustainability, 2019, 11(7): 1–20.

[8] 王戈, 卢杰, 于强, 等. 基于复杂网络理论的西藏巴宜区森林景观空间结构研究[J]. 农业机械学报, 2021, 52(4): 152–158.

[9] 侯宏冰, 郭红琼, 于强, 等. 基于LMBA策略的鄂尔多斯市生态空间网络优化[J]. 农业机械学报, 2021, 52(1): 219–227.

[10] YANG Haihua, AN Shi. Robustness evaluation for multi-subnet composited complex network of urban public transport[J]. Alexandria Engineering Journal, 2021, 60(2): 2065–2074.

[11] 楼洋, 李均利, 李升, 等. 复杂网络能控性鲁棒性研究进展[J]. 自动化学报, 2022, 4S(10):2374–2391.

[12] SURENDRA N, ANKUSH J, PRAMOD K S, et al. Mixed-noise robust face super-resolution through residual- learning based error suppressed nearest neighbor representation[J]. Information Sciences, 2021, 546: 121–145.

[13] WILKIE O, KARSTEN B, CATHERINE D S, et al. Stochasticity and robustness in spiking neural networks[J]. Neurocomputing, 2021, 419: 23–36.

[14] DE A C, GONCALVES S, DA C B. Empirical determination of the optimal attack for fragmentation of modular networks[J]. Physica A- Statistical Mechanics and its Applications, 2021, 563: 1–13.

[15] EBADI R, SADEGHI Y A, KAZEMZADEH R, et al. Techno-economic evaluation of transportable battery energy storage in robust day-ahead scheduling of integrated power and railway transportation networks[J]. International Journal of Electrical Power and Energy Systems, 2021, 126(PA): 1–19.

[16] SHEN Yi, REN Guang, ZHANG Ning, et al. Effects of mutual traffic redistribution on robustness of interdependent networks to cascading failures under fluctuant load[J]. Physica A: Statistical Mechanics and its Applications, 2020, 560: 1–10.

[17] 张晓琳, 金晓斌, 赵庆利, 等. 基于多目标遗传算法的层级生态节点识别与优化——以常州市金坛区为例[J].自然资源学报, 2020, 35(1): 174–189.

[18] 朱捷, 苏杰, 尹海伟, 等. 基于源地综合识别与多尺度嵌套的徐州生态网络构建[J]. 自然资源学报, 2020, 35(8): 1986–2001.

[19] 黄木易, 岳文泽, 冯少茹, 等. 基于MCR模型的大别山核心区生态安全格局异质性及优化[J]. 自然资源学报, 2019, 34(4): 771–784.

[20] 裴燕如, 武英达, 于强, 等. 荒漠绿洲区潜在生态网络增边优化鲁棒性分析[J]. 农业机械学报, 2020, 51(2): 172–179.

[21] 王戈, 于强, YANG Di, 等. 基于复杂网络分析法的层级生态网络结构研究[J].农业机械学报, 2019, 50(7): 258–266+312.

[22] 李恒凯, 王利娟, 肖松松. 基于多源数据的南方丘陵山地土地利用随机森林分类[J]. 农业工程学报, 2021, 37(7): 244–251.

[23] 许峰, 尹海伟, 孔繁花, 等. 基于MSPA与最小路径方法的巴中西部新城生态网络构建[J]. 生态学报, 2015, 35(19): 6425–6434.

[24] 胡其玉, 陈松林.基于生态系统服务供需的厦漳泉地区生态网络空间优化[J].自然资源学报, 2021, 36(2): 342–355.

[25] 荣月静, 严岩, 王辰星, 等. 基于生态系统服务供需的雄安新区生态网络构建与优化[J]. 生态学报, 2020, 40(20): 7197–7206.

[26] 郭家新, 胡振琪, 李海霞, 等. 基于MCR模型的市域生态空间网络构建[J]. 农业机械学报, 2021, 52(3): 275–284.

[27] ESTRADA E, ORJAN B. Using Network Centrality Measures to Manage Landscape Connectivity[J].Ecological Applications, 2008, 18(7): 1810–1825.

[28] 张远景, 柳清, 刘海礁. 城市生态用地空间连接度评价——以哈尔滨为例[J]. 城市发展研究, 2015, 22(9): 15–22+2.

[29] MATTHEW D, RONALD B, FERENC S. Simultaneous- direct blockmodeling for multiple relations in Pajek[J]. Social Networks, 2015, 40(1): 1–16.

[30] 莫振淳, 傅丽华, 彭耀辉, 等. 基于综合重要度评价的生态空间网络关键节点识别[J]. 湖南工业大学学报, 2018, 32(2): 64–69.

[31] NEWMAN M E J. Ameasure of betweenness centrality based on random walks[J]. Social Networks, 2005, 27(1): 39–54.

[32] 接婧. 国际学术界对鲁棒性的研究[J]. 系统工程学报, 2005, 20(2): 153–159.

[33] 傅丽华, 莫振淳, 彭耀辉, 等. 湖南茶陵县域生态空间网络稳定性识别与重构策略[J]. 地理学报, 2019, 74(7): 1409–1419.

[34] 赵山春. 基于复杂网络理论的城市公交网络可靠性研究. 中国安全科学学报, 2013, 23(4): 108–112.

[35] 张端. 具有持续性生态系统的网络拓扑结构[D]. 镇江: 江苏大学, 2016.

[36] 黄燕, 李华强, 黄涛, 等. 基于复杂网络和暂态能量函数的支路暂态脆弱性评估[J]. 电力系统保护与控制, 2014, 42(20): 69–74.

[37] ZHU Caishi, WANG Xiaoyan. Research on evaluation algorithm of key nodes in urban road traffic network based on complex network[J]. Journal of physics. Conference series, 2020, 1629(1): 1–7.

[38] 强强. 网络脆弱性以及鲁棒性理论的近期研究发展[J]. 上海理工大学学报, 2011, 33(3): 287–291.

[39] 吴明功, 叶泽龙, 温祥西, 等. 基于复杂网络的空中交通复杂性识别方法[J]. 北京航空航天大学学报, 2020, 46(5): 839–850.

[40] 许文雯, 孙翔, 朱晓东, 等. 基于生态网络分析的南京主城区重要生态斑块识别[J]. 生态学报, 2012, 32(4): 1264–1272.

[41] 赵萌, 张雪琦, 张永霖, 等. 基于景观生态学的城市生态空间服务提升研究——以北京市顺义区为例[J]. 生态学报, 2020, 40(22): 8075–8084.

[42] 邓金杰, 陈柳新, 杨成韫, 等. 高度城市化地区生态廊道重要性评价探索——以深圳为例[J]. 地理研究, 2017, 36(3): 573–582.

[43] 安军. 鲁棒性分析的方法论意义[J]. 科学技术哲学研究, 2011, 28(5): 26–30.

Robustness simulation and stability analysis of ecological network in Wuhan metropolitan area

HUANG Yue1,2, LI Hongbo1,*, OU Guoliang3

1.College of Public Administration, Huazhong Agricultural University, Wuhan 430070, China 2.Wuhan Yongye Cyber Energy Planning and Survey Company Limited, Wuhan 430061, China 3.School of Construction and Environmental Engineering, Shenzhen Polytechnic, Shenzhen 518055, China

Ecological networks show different robustness under different levels of damage or interference intensity, which is bound to cause the regional ecosystem risk. Based on the construction and identification of the ecological network of the Wuhan metropolitan area, the importance evaluation system of nodes and corridors was established, and the robust model was used to simulate the robustness changes under random interference scenarios to evaluate the stability of the ecological network. The results showed that: (1) Based on the complex network theory a topological network consisted by 117 nodes and 189 connecting lines was generated according to the ecological network of the Wuhan metropolitan area. The nodes with higher importance level accounted for 23.93%, which were mainly distributed in the central and northern part of the study area. The nodes with lower importance accounted for 51.28% of the total number of nodes, mainly distributed in the northwest and southeast of the study area. (2) The gravity model was used to determine the importance of ecological corridors. 17 important corridors were obtained, and 28 were general corridors. Important corridor had a great impact on the connectivity and stability of the ecological network. (3) The number and importance of nodes had a significant impact on the stability of the network. When the node failure rate was less than 50%, the ecological network stability change was small, and the overall stability was relatively high; when the node failure rate was between 50%-85%, the ecological network was extremely unstable; when the node failure rate reached 85%, the ecological network began to paralyze. (4) Based on the importance of ecological nodes and corridors and simulated results, differentiated management strategies for ecological node protection and corridor construction were proposed.

ecological network; stability; robustness; Wuhan metropolitan area

10.14108/j.cnki.1008-8873.2024.01.008

X171.4

A

1008-8873(2024)01-063-11

2021-07-30;

2021-09-17

国家自然科学基金项目(41871179, 42077432 ); 华中农业大学自主科技创新基金项目(2016RC014)

黄悦(1996—), 女, 湖北黄冈人, 硕士研究生, 主要研究方向为土地生态与土地经济, E-mail: 1028407741@qq.com

通信作者:李红波, 男, 博士, 教授, 主要从事土地生态与土地经济研究, E-mail: lihb20132013@163.com

黄悦, 李红波, 欧国良. 武汉城市圈生态网络鲁棒性模拟及稳定性分析[J]. 生态科学, 2024, 43(1): 63–73.

HUANG Yue, LI Hongbo, OU Guoliang. Robustness simulation and stability analysis of ecological network in Wuhan metropolitan area[J]. Ecological Science, 2024, 43(1): 63–73.