柔性铰接板振动视觉测量与小波神经网络控制

邱志成，刘一鸿，李 旻

（华南理工大学 机械与汽车工程学院，广东 广州 510641）

1 引言

航天器和卫星上一般带有对太阳定向的太阳电池帆板，用以获取足够的能源。太阳电池帆板是典型的可展开空间平板阵列结构，多个柔性板之间一般通过铰链相连［1］，具有低刚度、大跨度、阻尼较小等特点。在与航天器一同运动时，系统整体会产生刚柔耦合现象，往往表现出低频密集模态和非线性等复杂的结构动力学特性［2］。由于太空环境中无大气阻尼，在航天器姿态调整、变轨或受到微小扰动时，太阳能电池帆板可能发生强烈且复杂的振动，难以短时间内自然衰减［3］；如果不加以抑制，不仅会影响自身的工作状态，同时也会对航天器本体产生冲击，导致航天任务失败，甚至造成严重后果。所以，研究如何对柔性铰接板结构进行振动测量与主动控制具有重要意义。

基于模型设计的控制器的控制效果很大程度上取决于建立模型的准确性。柔性结构常用的理论建模方式有假设模态法和有限元分析法。Chai 等［4］为了研究复合格子夹芯板的非线性振动特性，利用哈密顿原理和假设模态法推导出结构的非线性运动方程。Wang 等［5］建立了由宏纤维复合材料贴片驱动的柔性板的有限元模型，用于振动控制。采用上述理论方法建立起来的系统模型，不可避免地与实际模型存在一定的误差。通过实验模型辨识可以进一步修正模型，改善控制器的控制效果。

振动检测用于获取系统的振动信号，一方面用于系统动态特性的研究，另一方面作为闭环控制中控制器的反馈输入。按照传感器与被测量对象的位置关系，检测方式可分为接触式和非接触式测量。接触式测量是传统的振动测量方法，主要包括应变计、加速度传感器和压电陶瓷传感器等。由于传感器与被测对象直接接触，会对被测对象附加物理效应，改变其固有特性。非接触式测量可以避免负载效应，测量范围大，主要包括激光位移传感器、光纤光栅传感器和机器视觉传感器等。Deng 等［6］采用改进的三维点立体视觉方法测量了悬臂梁的振动响应。马天兵等［7］将线结构光技术应用于柔性臂的振动检测，并采用优化后的PID 进行振动控制。Liu 等［8］提出了一种校正摄像机运动影响的方法，使用立体视觉系统精确测量机翼变形。陈磊等［9］采用三维立体视觉方法对高超声速风洞试验段环境飞行器的颤振进行测量。双目立体视觉作为传统振动测量技术的一个补充或替代，具有测量范围广、稳定性好和抗干扰能力强等优点。

柔性结构的振动抑制大多通过设计基于振动反馈信号的闭环控制器来实现。闭环控制主要包括线性控制、非线性控制和智能控制。其中，智能控制从本质上来说也是非线性控制的一种，具有自学习和自适应能力，相比线性控制更能适应系统的复杂性和不确定性，具有更好的稳定性。在智能控制中，模糊逻辑、神经网络和学习控制等广泛运用于振动领域。Song 等［10］针对悬臂梁结构，采用NARX 神经网络进行系统辨识和振动主动控制研究。Yang 等［11］针对柔性机械臂的轨迹跟踪和减振，提出了一种基于迭代学习的自适应分布式控制方法。作为智能控制的一种，小波神经网络（Wavelet Neural Network，WNN）用小波函数代替作为激活函数，融合小波的多分辨率分析特性和神经网络的自学习能力，具有较快的收敛速度，在系统辨识和控制等领域得到了广泛的应用［12］。Chen等［13］采用自适应WNN 对具有遗传非线性和时变特性的隔膜式气动隔振器系统进行控制，取得了良好的控制效果。而自回归小波神经网络（Self-Recurrent Wavelet Neural Network，SRWNN）由WNN 发展而来，结合递归神经网络（RNN）的吸引子动力学和WNN 的快速收敛的优点，引入自反馈环储存小波的历史信息，具有强大的非线性动态映射能力［14］。Ganjefar等［15］针对欧拉-伯努利梁结构设计了SRWNN 控制器进行振动抑制，并验证了控制的有效性和稳定性。刘斌等［16］提出一种采用SRWNN 的无人机反演控制方法，解决了因外界干扰和参数摄动引起的控制问题。

本文对移动柔性铰接板系统的振动检测和主动控制进行了研究。针对该系统进行了动力学建模和系统辨识，提出了一种双目视觉振动检测方法，设计了基于SRWNN 的控制器和振动主动控制方案。在此基础上进行了移动柔性铰接板的振动检测和控制实验研究，并与比例微分控制（Proportional-Derivative control，PD）进行比较，验证了双目视觉检测和SRWNN 控制方案的有效性。

2 移动柔性铰接板结构与建模

2.1 移动柔性铰接板系统

如图1 所示，移动柔性铰接板系统由柔性铰接板主体部分和视觉检测部分组成。其中，柔性铰接板主体部分由两块薄板通过柔性铰链铰接，固定在移动基座上，与电机滚珠丝杠模组的移动滑块相连。电机滚珠丝杠模组放置在实验底座上，通过伺服电机驱动滑块带动柔性铰接板做平移运动，滚珠丝杠导程为10 mm。电机选用型号为HC-KFS43 的三菱电机，配套的伺服驱动器型号为MR-J2S-40A。双目视觉检测部分主要包括两台Basler 工业相机和粘贴在柔性板平面的标志点阵，相机通过滑轨固定在铝型架上。

图1 移动柔性铰接板系统Fig.1 Translational flexible hinged plate system

柔性铰接板上粘有压电（PZT）传感器、压电驱动器和圆形标志点。柔性板产生振动形变后，PZT 传感器将它转化为电荷量，经电荷放大器转换为电压信号，通过端子板和运动控制卡A/D 转换传递给计算机，获得振动信号。同时，双目相机将采集到的标志点图像信号传输给计算机，运行相应的视觉处理算法获得振动信号。计算机接收得到振动信号后，通过控制算法计算出控制信号，并通过运动控制卡D/A 转换后，经电压放大器放大，输出到PZT 驱动器抑制振动。运动控制卡（固高科技公司，型号为GTS800-PV-PCI）具有8 路模数（A/D）转换和8 路数模（D/A）转换通道。压电驱动器的极限输出电压为±310 V，电压放大器的放大倍数为62。柔性铰接板和PZT 的尺寸参数和材料性能参数列于表1。

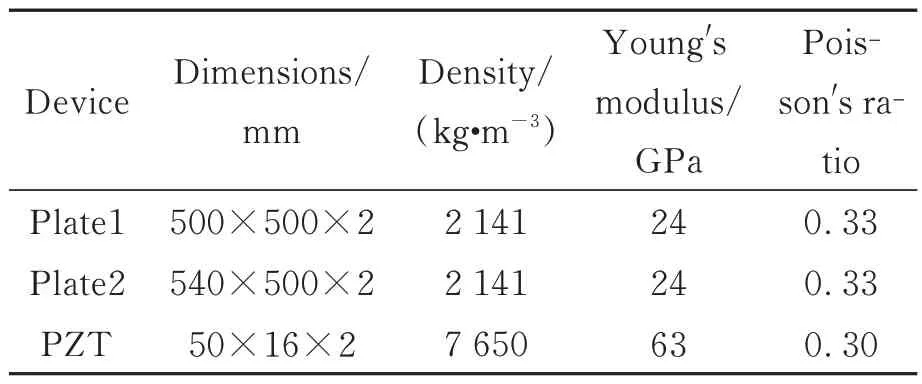
表1 柔性铰接板和PZT 的尺寸参数和材料性能参数［17］Tab.1 Dimensional and material performance parameters of flexible hinged plate and PZT patches

2.2 动力学建模和系统辨识

将柔性铰接板划分为有限个数的4 节点12自由度矩形单元，采用有限元法结合哈密顿原理，通过计算系统的总动能和总势能，得到移动柔性铰接板的动力学方程。在此基础上采用模态截断法，通过模态坐标变换得到包含前两阶弯曲模态的状态空间表达式为［17］：

为了获得相对精确的系统模型用于后续控制器设计，本文对模型参数进行了辨识。辨识结果如下：

3 双目视觉振动检测

双目视觉振动检测是一种非接触式全场测量手段，对大位移和低频振动具有良好的检测效果。本文针对双目视觉传感器设计了移动柔性铰接板系统的振动检测方案，该方案包括视觉系统标定、图像处理和振动信号解算等。

3.1 振动检测流程

针对移动柔性铰接板固定基座下和平移运动下的振动检测，采用双目立体视觉测量标志点位置变化来实现。其中，左右工业相机的分辨率均为1 920 pixel×1 200 pixel。所采用的标志点为柔性板上粘贴的标志点阵1，左边为3 个半径为6.5 mm 的小标志点，右边为1 个半径为9.5 mm 的大标志点，它们沿柔性板宽度方向的中线对称，如图2 所示。

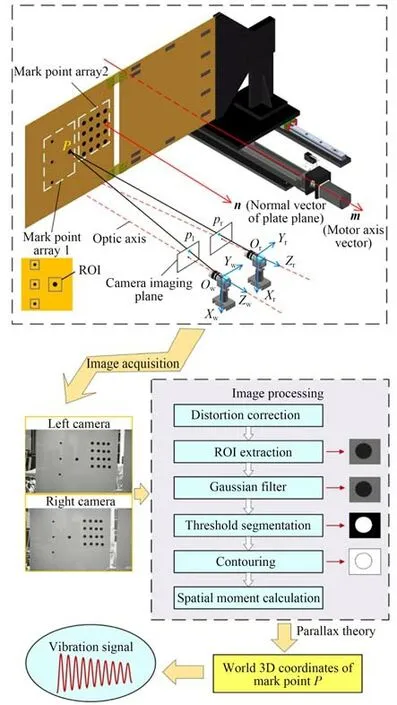
图2 双目视觉测振示意图Fig.2 Schematic diagram of vibration detection by binocular vision

在执行视觉检测程序后，在每个采样频率下，左右相机同时各采集一张图像。首先，对采集到的图像进行畸变校正来修正标志点的三维坐标信息；第二，设置感兴趣区域（Region of Interest，ROI），选取原则是在实验过程中，每个标志点始终保持在ROI 范围内，同时尽可能缩小ROI 面积，以减少后续图像处理的耗时；第三，对提取的ROI 进行高斯滤波以减少噪声的影响；第四，通过阈值分割进行二值化处理，只保留标志点信息；第五，采用Canny 边缘检测算法提取标志点轮廓，通过求解空间矩得到轮廓的二维重心坐标；最后，基于视差原理，将二维重心坐标通过标定得到的相机参数关系转换为世界三维坐标。

为了进一步获得振动信号，保持柔性铰接板静止，对前20 组计算得到的世界三维坐标计算平均值，作为标定点初始位置。通过计算与初始位置的欧氏距离可以获得后续标志点的位置变化量。当伺服电机驱动柔性铰接板做平移运动时，需要额外减去电机轴方向m上的刚体位移。

综上所述，柔性铰接板的振动表示为：

其中：为第k个标志点的振动量，为求解得到的柔性铰接板视觉检测的振动量；(xk，yk，zk)为第k个标志点当前时刻的世界三维坐标，(，)为初始位置的世界三维坐标；=(，，)，为归一化电机轴方向向量；s=，为编码器读取的电机转角换算成的刚体基座位移值。其中，θ为编码器速度积分得到的角位移，Dlead为滚珠丝杠导程。

3.2 系统标定

为了能够准确获得移动柔性铰接板的振动信息，首先对双目视觉系统进行标定，包括相机标定和电机轴标定。相机标定包括内参标定和外参标定。内参标定分别确定左右相机的内参矩阵，外参标定确定右相机相对于左相机的外参矩阵。本文采用张正友标定法［20］，借助MATLAB 相机标定工具箱对左右相机进行标定，标定过程如图3 所示。

图3 双目视觉相机标定Fig.3 Calibration of binocular vision cameras

针对移动柔性铰接板系统的平移运动中的振动检测，需要对电机轴方向m进行标定。由于相机视场不能覆盖刚体基座区域，本文采用柔性板静止时平面的法向量方向近似作为电机轴方向，通过求解柔性板平面法向量来标定电机轴。在相机标定得到准确的内外参后，利用3.3 节的方法，求解图2 中标志点阵2 所有标志点重心的世界三维坐标。针对获得的坐标，采用最小二乘法来拟合柔性板平面方程，进而求解出柔性铰接板平面的法向量。

3.3 世界三维坐标的获取

在分别得到标志点左、右相机图像的二维重心坐标后，可以通过视差原理将其转换为世界三维坐标。如图2 所示，对于大标志点P的重心，假设它在世界坐标系下的坐标为(xw，yw，zw)，在右相机坐标系下的坐标为(xr，yr，zr)，分别投影在左右相机成像平面上的图像坐标为pl(ul，vl)和pr(ur，vr)。为了便于得到二维图像坐标到三维世界坐标的转换关系，设世界坐标系与左相机坐标系重合，即(xw，yw，zw)=(xl，yl，zl)。

根据透视原理可以得到［18］：

P点在世界坐标系和右相机坐标系下的坐标满足［19］：

其中：R和T分别为相机外参矩阵中的旋转矩阵和平移向量，用以表征左右相机间的相对位置关系。

联立式（3）和式（4），得到关于[xwywzw]T的一个超定方程组：

通过最小二乘法求解奇异矩阵的伪逆来获得λ=[xwywzw]T的一个近似解：

其中：L为式（5）等号左部分的第一个矩阵，N为式（5）等号的右部分。

4 自回归小波神经网络控制器设计

4.1 控制器结构

SRWNN 具有结构简单、动态性好等特点。如图4 所示，该网络总共有4 层，由下至上分别为输入层、母波层、乘积层和输出层［21］。

图4 SRWNN 结构Fig.4 Structure of SRWNN

第一层是输入层，负责将输入元素传递到下一层。本文针对移动柔性铰接板系统的控制器设计共有2 个输入层神经元，表示为：

第二层是母波层，该层的每个节点（由虚线部分表示）都由等于输入元素个数的神经元组成，每个神经元包括一个带有自反馈回路的母小波。本文选用高斯小波函数φ(x)=-xexp(-0.5x2)作为母波层的激活函数。该层每个节点的小波φij可通过母小波变换而来，即：

其 中：zij=(oij-tij)/dij，tij和dij分别为平移因子和伸缩因子，ij表示第i个小波的第j个输入项；oij(k)为小波元k时刻的输入，表示为：

其中：θij是母小波自反馈回路的权重系数，代表对过去信息存储的比率。

第三层是乘积层，该层的每个神经元通过母波层各个节点的母小波的累乘得到：

其中Nw为母波层的节点个数。

第四层是输出层，包括1 个神经元，由输入层和乘积层输出结果的线性组合得到，可以表示为：

其中：wi和aj分别为乘积层和输入层到输出层之间的连接权系数。由于实际系统中常常需要限制控制电压，因此，本文采用双曲正切函数作为输出层的激活函数进行输出的归一化，即：

4.2 控制方案及网络更新

针对移动柔性铰接板前两阶弯曲模态振动，采用SRWNN 作为控制器进行系统的振动主动控制。图5 为系统控制流程。首先，基于辨识得到的前两阶弯曲模型，在仿真环境中分别构建一阶弯曲模态自回归小波神经网络控制器（SRWNNC-1b）和二阶弯曲模态自回归小波神经网络控制器（SRWNNC-2b）；其次，通过控制器与模型的交互不断进行网络训练，在每一时刻更新网络权重系数，直至收敛；最后，将训练好的模态控制器作用于实验系统，每阶模态控制器接收各自模态的振动反馈信号，输出相应的控制量到实验系统，抑制柔性铰接板的振动。

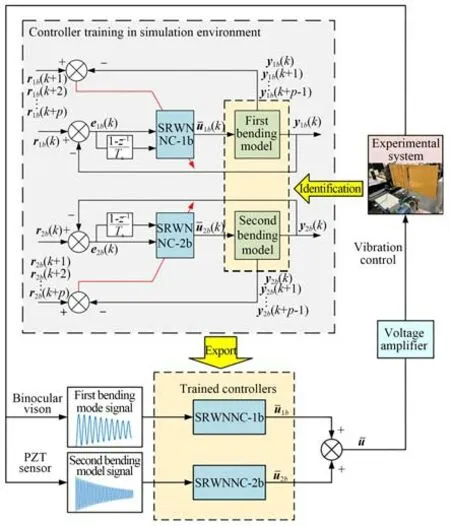
图5 SRWNN 控制流程Fig.5 Control flowchart of SRWNN

控制器网络采用多步更新方式，在当前时刻通过辨识模型和控制器网络多次交互得到未来多步的结果，并基于目标函数进行更新。目标函数为：

其中：误差矩阵E(k)=R(k)-Y(k)，k时刻的多步期望值为R(k)=[r(k+1)…r(k+p)]T，k时刻通过辨识模型输出的多步结果为Y(k)=[y(k)…y(k+p-1)]T；U(k)=[(k)…(k+p-1)]T，为k时刻控制网络的多步输出结果；Qe和Qu分别为各步误差和电压的权重矩阵。

采用梯度下降法更新网络权重系数，从而最小化目标函数。更新过程可以表示为：

在保证SRWNNC 训练具有稳定性的同时，为了能够获得最大的收敛速度，本文采用自适应学习率（Adaptive Learning Ratio，ALR）方法来确定每一时刻的更新步长［22］。网络中每一种权 重系数对应的学习率可表示为：

其中Ni为控制器网络输入层的神经元个数，本实验中取值为2。

5 实 验

5.1 标定结果

采用3.2 节所述方法进行标定，分别得到双目相机内外参模型和电机轴方向矢量。双目相机内参模型参数如表2 所示，外参模型用齐次变换矩阵表示为：

表2 双目相机外参模型参数Tab.2 Extrinsic parameters of binocular cameras

在相机三维坐标下，求解得到的归一化柔性板平面法向量为=[0.046 6 0.026 6 0.998 6]T，用此结果作为电机轴的归一化方向矢量的近似，并参与振动位移求解。

5.2 控制网络训练结果

由于小波函数具有向两侧快速衰减的特点，如果小波的伸缩因子太小，小波可能过于局部化；如果平移因子选择不当，则小波可能位于ROI 之外。因此，本文采用Oussar［23］推荐的方法合理地初始化SRWNN 网络的权重系数。

训练参数的设置很大程度上影响控制网络的收敛速度。母波层的节点个数Nw均设为10，网络多步更新的步数选择为2。SRWNNC-1b 的训练总周期为2 000 次，各步误差权重矩阵Qe_1b=diag[1 1 0.5 0.5]，各步电压权重矩阵Qu_1b=diag[0.02 0.01]；SRWNNC-2b的训练总周期为1 200 次，各步误差权重矩阵Qe_2b=diag[1 1 0.5 0.5]，各步电压权重矩阵Qu_2b=diag[0.02 0.01]。各权重系数的学习率由式（17）实时计算得出。

SRWNNC 的训练曲线如图6 所示。从图中可知，目标函数值呈下降趋势直至收敛。

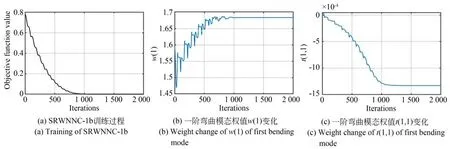
图6 SRWNNC 训练Fig.6 Training of SRWNNC

5.3 仿真和实验结果

为了验证双目视觉振动检测和SRWNNC 的有效性，将训练好的SRWNNC 导出作用于移动柔性铰接板实验系统，并选用大增益PD 控制器作为对比。为了确保实验结果的有效性，实验用到的滤波器参数保持一致，包括滤波器参数和PD 增益参数。在保证柔性铰接板初始振动状态相同的情况下，要求PD 控制输出的电压与SRWNNC 具有相同的饱和周期。多次调整选取控制效果最好的PD 增益参数为kp=0.2，kd=0.1。

本实验重点研究移动柔性铰接板的一阶弯曲模态。由于图像处理耗时过长，限制相机的采样频率为50 Hz，避免程序处理超时。因此，双目视觉只能检测一阶弯曲模态信号，作为反馈信号通过SRWNNC-1b 控制器进行控制。与此同时，二阶弯曲模态信号采用压电传感器检测，采样频率为200 Hz，并参与反馈由SRWNNC-2b 控制器进行控制。在此基础上，分别进行了固定基座和梯形轨迹运动情况下的移动柔性铰接板系统振动控制实验。

自由振动实验如图7 所示，在柔性铰接板自由端施加激励使它产生一阶弯曲模态振动，在不加任何控制的情况下，采用双目视觉方式实时检测振动信号，通过式（2）计算得到振动位移。图7（a）为前120 s 的自由振动位移曲线。可以看出，在不施加控制下，柔性铰接板振动会持续很长一段时间。为了验证双目视觉测振的精度，采用相同频率的正弦曲线对图7（a）中振动曲线105～120 s 之间的部分进行拟合，结果如图7（b）所示。可以看出，在0.1 mm 左右振动曲线仍能保持较完整光滑的正弦形状，并且通过计算得到的拟合平均误差很小，为0.015 5 mm，由此验证了双目视觉的振动测量精度小于0.1 mm，满足实验系统的测量要求。

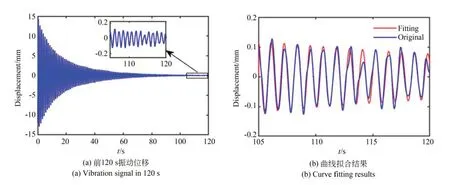
图7 一阶弯曲模态自由振动实验结果Fig.7 Free vibration experimental result of first bending mode

图8 为基座固定时的SRWNNC 和PD 控制的对比仿真和实验。图8（a）和8（b）为一阶弯曲模态振动的仿真结果。图8（c）和8（d）为一阶弯曲模态振动的实验结果，其中振动位移信号由双目视觉测得，控制电压通过视觉位移信号反馈得到。为了更好地分析实验结果，设定振动位移在0.1～1 mm 内属于小幅值信号，小于0.1 mm 的振动被完全抑制。可以看出，仿真和实验结果基本一致。在SRWNNC 实验中，柔性铰接板系统振动在12 s 左右被完全抑制，而在大增益PD 控制开始20 s 后，仍然存在小幅值振动。

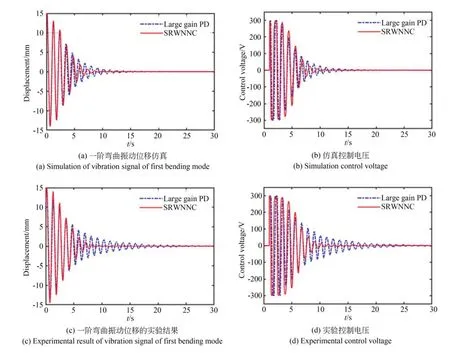
图8 固定基座压电主动控制仿真和实验结果Fig.8 PZT active control simulation and experimental results under fixed base

为了验证柔性铰接板做平移运动过程中的振动视觉测量和控制效果，规划了1 s 50 mm（时间参数为1 s，距离参数为50 mm）的梯形轨迹。在不加任何控制下，设置1 s 后电机开始驱动柔性铰接板进行梯形轨迹平移运动实验，经过1 s 后走完轨迹，在此期间和之后30 s 的振动信号如图9（a）所示。可以看出，柔性铰接板在运动中主要激起一阶弯曲模态。通过实时计算基座刚体位移，能够很好地将柔性铰接板平移运动中的振动信号解耦出来，验证了双目视觉和电机轴标定结果的有效性。此外，还进行了1 s 50 mm 梯形轨迹运动的压电主动控制仿真和实验，结果分别如图9（b），9（c）和图9（d），9（e）所示。可以看出，仿真和实验结果基本一致。在SRWNNC 实验中，梯形轨迹运动下振动在13 s 左右被完全抑制，而在大增益PD 控制下振动在20 s 后还有小幅值信号，直到26 s 左右才完全抑制。SRWNNC 能够快速抑制振动，尤其是小幅值阶段，展现出比大增益PD 更好的抑振效果。

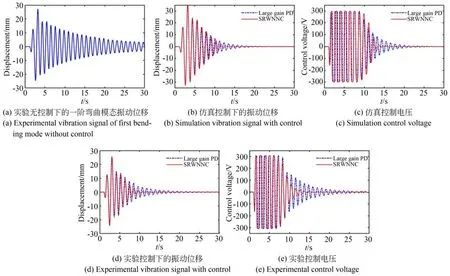
图9 梯形轨迹平移运动下的仿真和实验结果Fig.9 Simulation and experimental results under translation motion of trapezoidal trajectory

为了更直观地展现控制器的振动抑制效果，绘制了前30 s 实验振动信号的功率谱密度（Power Spectral Density，PSD），如图10 所示。从图中可以看出，振动信号的主要频率分布在峰值点0.854 5 Hz 附近，对应着柔性铰接板的一阶弯曲模态频率。SRWNNC 和PD 控制下的峰值功率均低于自由振动。特别地，SRWNNC 控制下的峰值功率低于PD 控制，验证了SRWNNC 比PD控制能够更好地抑制一阶弯曲模态频率上的振动能量，控制效果更优。

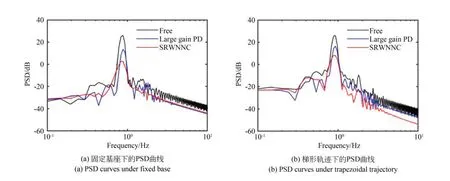
图10 实验振动信号的功率谱密度分析对比Fig.10 Comparison of PSD of experimental vibration signals

在振动反馈控制方面，大增益PD 控制器和SRWNNC 都能够有效地抑制移动柔性铰接板系统的振动。大增益PD 控制需要通过移相来解决信号滤波带来的控制量相位滞后问题，且控制电压在小幅值振动时的输出能力不足，衰减较慢。然而，SRWNNC 的神经网络具有强大的泛化能力和非线性特性，能够补偿系统的不确定性和非线性因素，不仅使大幅值振动快速衰减，小幅值振动时也能输出较大的控制电压，迅速抑制振动。

6 结论

本文研究了基于双目视觉检测和反馈控制的移动柔性铰接板实验系统，建立了系统的有限元模型，并通过辨识得到校正后的系统模型参数。然后，提出了一种双目视觉结合标志点的移动柔性铰接板振动测量方法，进行了双目相机标定、图像处理和振动提取实验研究。基于辨识模型设计并训练了SRWNNC。为了验证所述振动检测和控制方法的有效性，将视觉检测的振动信号进行反馈，分别进行了固定基座和轨迹运动下SRWNN 控制和大增益PD 控制的仿真和实验对比。仿真和实验结果表明，双目视觉检测振动具有良好的测量精度，能够很好地进行反馈控制，SRWNN 控制由于具有强大的非线性特性，展现出比PD 控制更加出色的抑振效果。