经典单排管冻结温度场的瞬态适用性研究

缪茂秋

（南京天京建筑工程监理事务所，江苏南京 210004）

0 引言

近年来，人工冻结法在地下空间开发利用中得到越来越多的应用。由于人工冻土的温度场分布理论是冻结法理论的基础之一，所以对于温度场的研究非常重要，各国学者也对单排冻结管的温度场进行了深入的研究，比如苏联的特鲁巴克公式[1]、巴霍尔金公式[2]，美国的Sanger &Sayles 公式[3]，日本建设机械化协会总结的公式[4]，以及中国的“成冰公式”等[5]。研究和实际工程应用表明，巴霍尔金温度场计算理论是上述各种温度场理论中计算结果最为精确的[6]。

然而，目前的研究主要针对温度场的静态分析，而并没有进行瞬态分析。本文研究了通过巴霍尔金公式计算得到的瞬态温度场，并与通过数值计算得到的实际温度场进行比较，来探讨影响巴霍尔金公式准确性的因素，以期为巴霍尔金公式在实际工程建设中的应用提供理论指导。

1 巴霍尔金冻结温度场

巴霍尔金冻结温度场模型是以冻结管成直线布置为基础的，以经典的单排管冻结为例，其冻结模型示意图如图1 所示。在地层结冰温度为0 ℃的假设条件下，冻土内部温度分布的计算公式可以表示为：

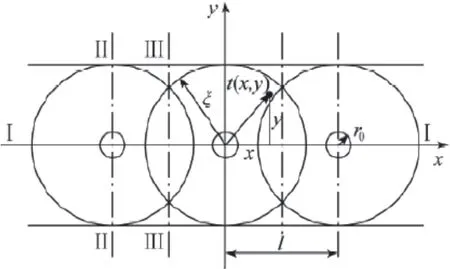
图1 巴霍尔金经典单排管冻结示意图

式（1）中，t(x, y)表示冻结区域内任一点的温度，℃；tCT表示冻结管内盐水温度，℃；r0表示冻结管半径，m；ξ 表示冻土厚度，m；l表示冻结管间距，m。

为了便于描述，在图1 冻结壁上选取3 个特征面：轴面（Ⅰ-Ⅰ），即y=0 的面；主面（Ⅱ-Ⅱ），即x=0 的面；界面（Ⅲ-Ⅲ），即x=l/2 的面。

2 单排管冻土温度场数值模拟

为了对单排管巴霍尔金公式进行瞬态分析，须知道某一时刻冻土帷幕的厚度。由冻土帷幕的厚度，可推算得到冻结管的温度场。因此，首先采用数值模拟得到不同时刻冻土帷幕的厚度。由于Abaqus 软件在热力学计算中可以清晰反映冻结壁的瞬态温度场，并与实际的分析结果较为吻合，故采用Abaqus 作为数值模拟的软件。模型以及参数介绍如下：

1）模型为宽20 m 的矩形平板，在中间竖直线上以1 m 为间距建立3 根冻结管模型，冻结管直径采用工程中常用的0.108 m，模型如图2 所示；2）初始土层温度为18 ℃，冻结管表面施加随时间变化的荷载，10 天降到-26 ℃，14 天降到-30 ℃，上下边缘设为绝热边界，左右边缘为固定温度18 ℃；3）土体材料相关参数如表1 所示；4）单元采用4 节点热分析单元DC2D4；5）计算时间为60 天。

图2 数值模型示意图

表1 土体材料参数

3 巴霍尔金公式与数值模拟对比分析

3.1 冻结壁厚度

通过数值计算，可得到冻土帷幕厚度随时间的发展如图3所示。根据计算结果，代入公式（1）就可以得到对应时间的巴霍尔金公式的温度场。

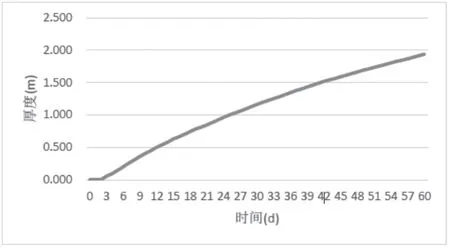
图3 冻结壁厚度发展曲线

对于界面区冻土厚度的发展，数值计算结果与巴霍尔金公式的计算结果比较见图4。

图4 界面区冻土厚度发展曲线对比

可以看出，在冻结早期巴氏公式的计算结果要大于数值模拟结果。随着时间的增加，二者之间的差值逐渐变小。其原因是，对于巴氏公式来说，冻土帷幕是一条平行于冻结管轴线的直线，主要参考主面的冻土厚度。而实际冻结过程中，主面冻结厚度在冻结初期要比界面发展得快，所以对于界面的冻土厚度来说，巴氏公式的计算结果要大于数值模拟的结果。

3.2 主面温度分析

在单排冻结管的主面上选取等距的三个计算点，距离冻结管中心的距离分别为0.5 m，1.0 m 和1.5 m，分别比较在数值模拟和巴氏公式计算条件下温度随时间的变化关系，计算结果如图5—图7 所示。

图5 主面上距离冻结管0.5 m 处温度发展曲线

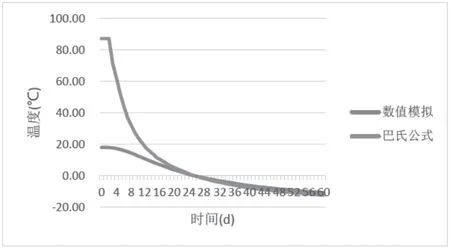
图6 主面上距离冻结管1.0 m 处温度发展曲线

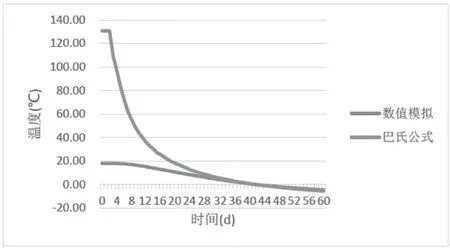
图7 主面上距离冻结管1.5 m 处温度发展曲线

由图5—图7 可以看出，当观测点处于正温区时，数值模拟结果同巴氏公式计算结果偏差较大。初始偏差最大，随着时间的增加，偏差减小直至接近于一个稳定值。初始阶段误差较大的原因主要是，巴氏温度场的推导是假设计算点的温度处于负温区。故当计算点位于正温区时，误差很大。当计算点位于负温区后，随着时间的延长，数值模拟与巴氏公式计算结果之间的差值基本趋于一个稳定值。通过比较以上3 图可以发现，计算点距离冻结管越远，稳定偏差就越小。

3.3 界面温度分析

在单排管界面上选取3 个计算点，距离冻结管轴线的距离分别为0.0 m，0.864 m 和1.404 m。选取这三点的原因可参照图1，当冻结圆柱半径分别为0.5 m，1.0 m 和1.5 m 时，界面区冻土厚度分别为0.0 m，0.864 m 和1.404 m。分别比较在数值模拟和巴氏公式计算条件下温度随时间的变化关系，计算结果如图8—图10 所示。

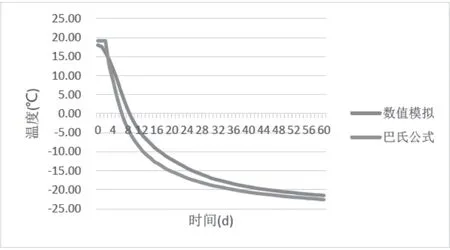
图8 界面上距离冻结管轴线0.0 m 处温度发展曲线

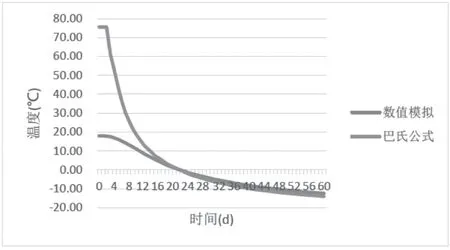
图9 界面上距离冻结管轴线 0.864 m 处温度发展曲线

图10 界面上距离冻结管轴线1.404 m 处温度发展曲线

观察以上三图可以得到与主面类似的结论，即当计算点处于正温区时，数值模拟结果同巴氏公式的计算结果偏差较大。当计算点位于负温区后，数值模拟与巴氏公式计算结果之间的差值基本趋于一个稳定值。并且计算点距离冻结管轴线越远，数值结果同巴氏结果之间的差值就越小。

4 误差分析

通过以上计算可以发现，无论计算点处于何位置，数值结果与巴氏公式计算结果之间的误差最终都会趋向于一个稳定值。接下来主要探讨影响这个稳定值大小的因素。考虑冻结温度场的热传导控制方程：

根据热传导公式可以看出土体的导热过程与热传导系数、密度和比热有较大关系。同时，冻结管之间的间距也会对冻土温度场的分布产生较大的影响，故接下来将探讨以上几个方面对公式的影响。

4.1 热传导系数

取主面上距离冻结管中心为1.0 m 处的计算点，冻结管的间距取为1.0 m，土体的密度及比热采用表1 所给的值。考虑以下三种情况：正常土体导热系数λ，较小的导热系数0.1λ，以及较大的导热系数10λ（λ 为表1 中的导热系数）。分别比较以上三种情况下数值模拟与巴氏公式的计算结果，如图11—图13 所示。

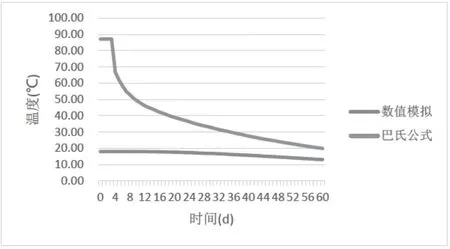
图11 热传导系数为0.1λ 温度发展曲线

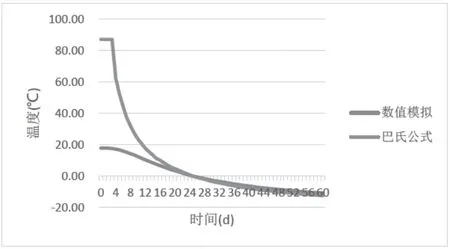
图12 热传导系数为λ 温度发展曲线

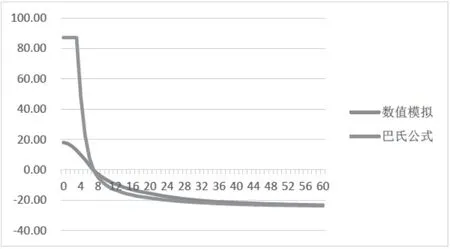
图13 热传导系数为10λ 温度发展曲线

可以清楚地看出，随着时间延长，数值模拟与巴氏公式之间的差值逐渐变小。其中热传导系数越大，二者之间的差值就越小。在60 d，导热系数为10λ 时，稳定偏差值为0.5 ℃；导热系数为0.1λ 时，稳定偏差值为6.8 ℃。故热传导系数是影响巴氏公式产生偏差的原因之一。

4.2 冻结管间距

选取主面上距离冻结管中心为1.0 m 处的计算点，分别考虑冻结管间距为0.5 m，1.0 m 和1.5 m 三种情况，其余参数参照表1。分别比较以上三种情况下数值模拟与巴氏公式的计算结果，如图14—图16 所示。

图14 冻结管间距为0.5 m 温度发展曲线

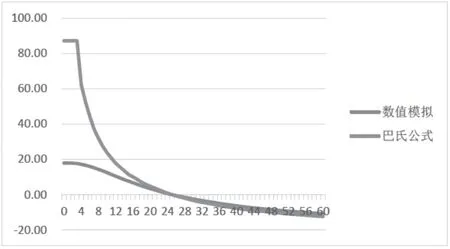
图15 冻结管间距为1.0 m 温度发展曲线

图16 冻结管间距为1.5 m 温度发展曲线

可以看出，随着时间的增加，数值模拟与巴氏公式之间的差值在逐渐变小。其中，冻结管之间的间距越小，二者之间的差值就越小。在60 d，冻结管间距为0.5 m 时，稳定偏差值为0.8 ℃；导热系数为1.5 m 时，稳定偏差值为2.0 ℃。故冻结管间距也是影响巴氏公式产生偏差的原因之一。

4.3 土体密度

由热传导公式（3）可以看出，土体密度和土体比热对热传导的影响是类似的。故在本文中仅考虑土体密度的影响。选取主面上距离冻结管中心为1.0 m处的计算点，考虑以下三种情况：正常土体密度ρ，较小的导热系数0.1ρ，以及较大的导热系数10ρ。其他参数的选取参照表1，分别比较以上三种情况下数值模拟与巴氏公式的计算结果，如图17—图19 所示。

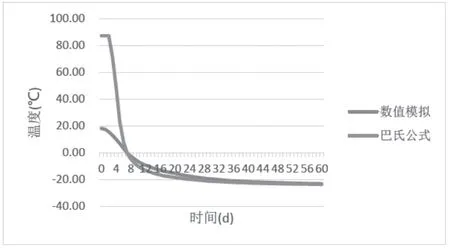
图17 密度为0.1ρ 温度发展曲线

图18 密度为ρ 温度发展曲线

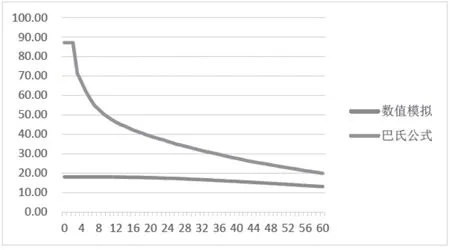
图19 密度为10ρ 温度发展曲线

从以上三图可以看出随着时间的增加，数值模拟与巴氏公式之间的差值在逐渐变小。其中，土体密度越小，二者之间的差值就越小。在60 d，土体密度为0.1ρ 时，稳定偏差值为0.5 ℃；导热系数为10ρ 时，稳定偏差值为6.9 ℃。故土体密度也是影响巴氏公式产生偏差的原因之一。

5 结语

总体来说，对于负温区巴霍尔金单排管公式具有较好的精度，能够满足工程上的需求。并且当测点远离冻结管时，误差较小。影响误差的主要因素有土体的热传导系数、冻结管之间的间距、土体的密度及比热。当土体的热传导系数变大时，数值模拟与巴氏公式间的误差变小；当冻结管之间的间距变小时，数值模拟与巴氏公式间的误差变小；当土体的密度、比热容变小时，数值模拟与巴氏公式间的误差变小。