对大初速舰炮炮弹跟踪能力需求分析

许俊飞，吴 玲，张朱峰，卢发兴

（海军工程大学兵器工程学院，武汉 430033）

0 引言

新型舰炮武器拥有能量可控、初速大、打击范围大、毁伤效能高等诸多优点［1］。在近程防空反导方面有着良好的弹道特性，尤其当高速动能武器采用制导炮弹时，可融合普通弹药和防空导弹的优点，使得对空反应速度更快、精度更高，能有效提升对空中目标的拦截能力。采用指令制导方式的防空制导炮弹，要求雷达能准确捕捉并跟踪飞离炮口的弹丸，从而计算弹目偏差并引导至弹上雷达开机点或引导至目标［2］。由于新型舰炮武器系统发射弹丸的初速大，因此，对观测设备的跟踪能力提出了很高的要求，尤其在弹丸刚出炮口的一段时间内，由于观测设备跟踪角速度的限制，将可能产生跟不上弹丸的问题［3］。本文针对大初速舰炮武器的炮弹跟踪问题，首先建立观测设备对炮弹方位和高低跟踪死区模型，明确跟踪死区与弹丸速度、高度、观测距离，以及观测设备最大跟踪角速度之间的关系，进而给出对大初速炮弹实现有效跟踪的观测设备能力需求。

1 炮弹运动角速度模型

新型舰炮武器系统发射炮弹的初速较大，由于受提供舰炮信息保障的观测设备性能所限，可能产生观测设备不能有效跟踪炮弹的现象［4］。观测设备在水平方向上不能跟踪瞄准炮弹的空域，称为观测设备方向跟踪死区，在垂直方向上不能跟踪的称为高低跟踪死区。跟踪死区的形成不仅与观测设备的最大跟踪角速度、观测距离有关，还与所跟踪目标，即炮弹的速度、高度等因素有关［5］。

假定在较短时间内，炮弹从炮口飞离并做等速、直线运动，O为观测设备位置，A0为炮口位置，φ为炮管倾角，d0为初始观测距离，Vm为炮弹速度，H为炮口相对观测设备的高度，A为炮弹现在点位置，d为炮弹水平距离，S为炮弹从初始点A0到现在点A的连线距离，S0、Sh分别为S在水平和垂直面上的投影，Qm为炮弹水平弹道相对于观测跟踪线的夹角，炮弹相对于O点的运动方向角速度和高低角速度分别为ωβ和ωε。

不妨假设炮弹水平弹道S0与初始观测距离d0垂直（否则可以通过发射方位角对d0进行转换计算），则由图1 可知，炮弹出炮口时相对观测设备的方向角β为

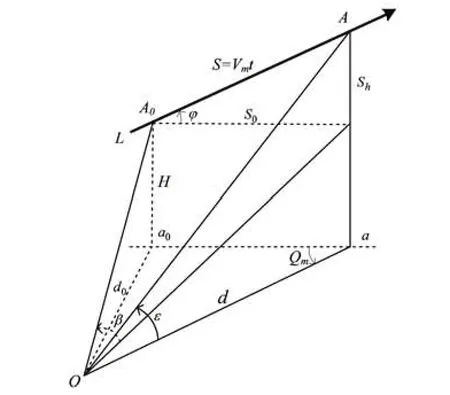
图1 炮弹运动角速度模型Fig.1 Angular velocity model of projectile motion

此时炮弹相对观测设备具有最大的方向角速度ωβ。

炮弹高低角ε为

类似可得炮弹高低角速度ωε为

2 观测设备跟踪死区模型

2.1 方向跟踪死区模型

为保障新型舰炮武器系统防空作战能力的发挥，观测设备需持续对炮弹进行跟踪［6］，假设观测设备的最大方向跟踪角速度为ωβg，炮弹运动的方向角速度为ωβ，因此，只要有ωβg≥ωβ，则观测设备在水平方向上就能跟踪目标，反之则无法跟踪，形成了水平方向的动态跟踪死区。

通常是以炮弹最大的方向角速度来确定方向跟踪死区［7］，在炮弹水平弹道垂直于初始观测距离时，由式（2）可知，当d=d0时，即炮弹出炮口瞬间相对观测设备具有最大的方向角速度ωβ，令其等于观测设备方向跟踪角速度，即

满足上式的初始水平观测距离d0即为给定炮弹水平初速时最坏情况下，恰好能跟上弹丸的观测距离，由式（2）可知

同时满足式（5）和式（6）特定的d0是恰好能跟得上炮弹的初始观测距离，如果d0减小一点，则ωβ将增大，使得ωβg＜ωβ，水平方向上观测设备不再能跟上炮弹，形成方向跟踪死区［7］；如果d0再大一点，则跟得上炮弹因而不存在跟踪死区；因此，方向跟踪死区在某一高度上为一圆域，设其半径为rβg，其值即为由式（5）和式（6）所决定的d0值，可得

运用无人机遥感技术，可以对地面情况最为快速便捷地进行获取。在进行测绘工作时，将无人机作为载体，在无人机主机上安装高分辨率摄像头，可以将地面的情况高精度的传输回来，成本较低，操作简单。并且具有极高的速度以及清晰度，便于使用，和传统的航拍技术相比更具有实用性。和传统遥感相比，无人机机动灵活，快速出击的响应能力，对于应急措施有着至关重要的作用。传统遥感数据缺少准确性，无人机遥感平台可以传输更加清晰的图像，从而进行更加精准的数据分析。目前无人机遥感技术在景观生态，地质灾害，环境保护，地理测绘领域中都有着广泛应用。

可见，在某一高度H上观测设备在方向上是否进入对炮弹的跟踪死区［8］，与炮弹水平速度分量Vmcosφ、观测设备的最大方向跟踪角速度ωβg，以及实际的初始观测距离d0有关。

当d0≥rβg，此时ωβg≥ωβ，不存在方向跟踪死区。

当d0＜rβg时，形成方向跟踪死区，死区半径为rβg。

特殊的当d0=0 时，由于此时炮弹运动对观测设备不产生方位角变化，也不存在方向跟踪死区［9］。

2.2 高低跟踪死区模型

由式（4）可知，炮弹高低角速度受多个因素的综合影响，计算较为复杂［10］。随着炮弹高度的增加，炮弹的高低角速度是在不断减小的，因此，对观测设备的跟踪能力要求也在不断减小，通常是以炮弹最大的高低角速度来确定高低跟踪死区，当d=d0时，以炮弹出口瞬间对炮弹的高低跟踪角速度作为判断依据，以此来计算对观测设备的高低跟踪死区模型［11］。

为实现对炮弹的稳定跟踪，设观测设备的最大高低跟踪角速度为ωεg，只要满足

观测设备在高度上就能跟踪炮弹，反之则不行。设高低跟踪死区半径为rεg，因此

当d0≥rεg，此时ωεg≥ωε，不存在高低跟踪死区。

当d0＜rεg时，形成高低跟踪死区，死区半径为rεg。

2.3 观测设备跟踪死区的确定

观测设备对炮弹进行跟踪时，在给定高度H上只要进入方向跟踪死区或高低跟踪死区之一，就无法有效跟踪弹丸［12］。因此，在计算观测设备跟踪死区时，采取如下步骤：

1）在初始条件下，确定方向跟踪死区以及高低跟踪死区；

2）根据方向、高低跟踪死区确定对炮弹稳定跟踪的方向、高低跟踪距离点；

3）在方向、高低跟踪距离点中取较大值，综合确定跟踪距离点。

3 仿真分析

观测设备对炮弹的跟踪死区影响因素多，模型复杂，为了验证跟踪死区模型的有效性，本章在典型作战想定下对跟踪死区模型及相关计算方法进行仿真分析。

3.1 跟踪死区变化趋势仿真分析

假定炮弹出口后，在一定时间内以恒定速度Vm运动，分别仿真分析炮弹的飞行速度Vm、初始观测距离d0，以及观测设备的最大方向、高低跟踪角速度ωβg、ωεg对跟踪死区半径rβg、rεg的影响。

1）跟踪死区半径rβg、rεg大小随炮弹速度Vm的变化关系

设观测设备最大方向跟踪角速度ωβg为35°∕s，炮弹出口高度H=10 m，倾角φ=30°，飞行速度Vm在1 000～2 500 m∕s 之间，仿真分析在不同初始观测距离d0条件下方向跟踪死区半径rβg随炮弹速度Vm的变化趋势，如图2所示。

图2 方向跟踪死区半径随目标速度变化关系图Fig.2 The change relationship diagram between the dead zone radius of direction tracking and the target speed

由图2 可知，当初始观测距离较小时（d0=10 m和d0=100 m），无论炮弹速度多大，都一直会存在方向跟踪死区；当初始观测距离较大且炮弹速度比较小时，不存在方向跟踪死区，随着炮弹速度的增大，方向跟踪死区半径越来越大。

设观测设备最大高低跟踪角速度ωβg为35°∕s，在上述条件下，仿真分析在不同初始观测距离d0条件下高低跟踪死区半径rβg随炮弹速度Vm的变化趋势，如图3所示。

图3 高低跟踪死区半径随目标速度变化关系图Fig.3 The change relationship diagram between the radius of elevation tracking dead zone and target speed

从图3 可以看出，高低跟踪死区的变化趋势同理方向跟踪死区。

2）跟踪死区半径rβg、rεg随最大跟踪角速度ωβg、ωεg的变化关系

在1）的初始条件下，设初始观测距离d0为1 000 m，最大方向跟踪角速度ωβg为0～70°∕s，仿真分析不同炮弹速度下，方向跟踪死区半径rβg随最大方向跟踪角速度ωβg、ωεg的变化趋势。

由图4、图5 可知，跟踪死区半径与观测设备最大跟踪角速度成反比，与炮弹速度成正比，当观测设备最大跟踪角速度足够大时，不存在跟踪死区。

图4 方向跟踪死区半径随观测设备最大方向跟踪角速度变化关系图Fig.4 The change relationship diagram between the radius of direction tracking dead zone and the maximum direction tracking angular velocity of observation equipment

图5 高低跟踪死区半径随观测设备最大高低跟踪角速度变化关系图Fig.5 The relationship between the radius of elevation low tracking dead zone and the maximum elevation tracking angular velocity of observation equipment

3）跟踪死区的三维仿真分析

设观测设备最大方向跟踪角速度ωβg为35°∕s，炮弹飞行速度Vm为1 500 m∕s，仿真分析实际方向跟踪死区。

由图6可知，对于方向跟踪死区，在不同初始观测距离下，模型计算得到的死区半径正好是实际死区的边界，证明了方向跟踪死区模型的有效性。由图7可知，随着高度的增加，方向跟踪死区在不断地减小，初始观测距离影响着方向跟踪死区的大小，当在观测设备的跟踪范围内，初始观测距离大到一定程度时，方向跟踪死区不存在。

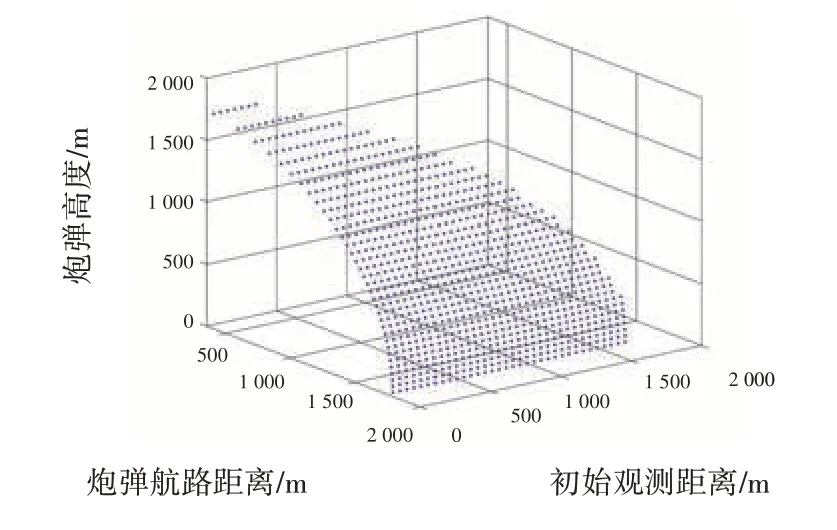
图6 不同条件下方向跟踪死区轮廓Fig.6 Dead zone contour of direction tracking

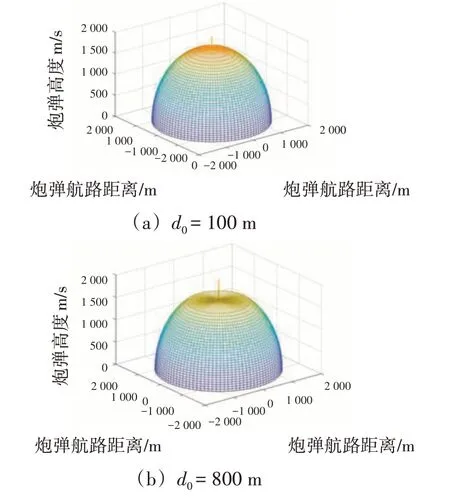
图7 不同d0条件下方向跟踪死区随炮弹高度变化趋势图Fig.7 Trend chart of direction tracking dead zone changing with projectile height under different d0 conditions

3.2 对炮弹跟踪能力需求仿真分析

在给定的弹丸初始速度Vm、高度H、炮管倾角φ，以及最大跟踪角速度ωβg和ωεg的条件下，只要调整初始观测距离d0，即可避开对弹丸的跟踪死区。在本舰观测条件下，可以通过在弹丸弹道上预设观测点O'，使指向该点的初始跟踪距离满足d0设置的要求，则在此观测点后观测设备可始终跟踪弹丸；在外部协同平台观测条件下，可通过增大初始观测距离d0，来实现对高初速弹丸的有效跟踪。

3.2.1 本舰观测设备跟踪

对于本舰观测设备，如图8所示，与本舰舰炮武器相比水平捷径比较小，设初始观测距离d0为10 m，观测设备最大方向跟踪角速度ωβg为35°∕s，最大高低跟踪角速度ωεg为25°∕s，炮管倾角φ=45°，炮弹飞行速度Vm为1 000 m∕s、1 500 m∕s、2 000 m∕s、2 500 m∕s时进行仿真分析，结果如表1所示。

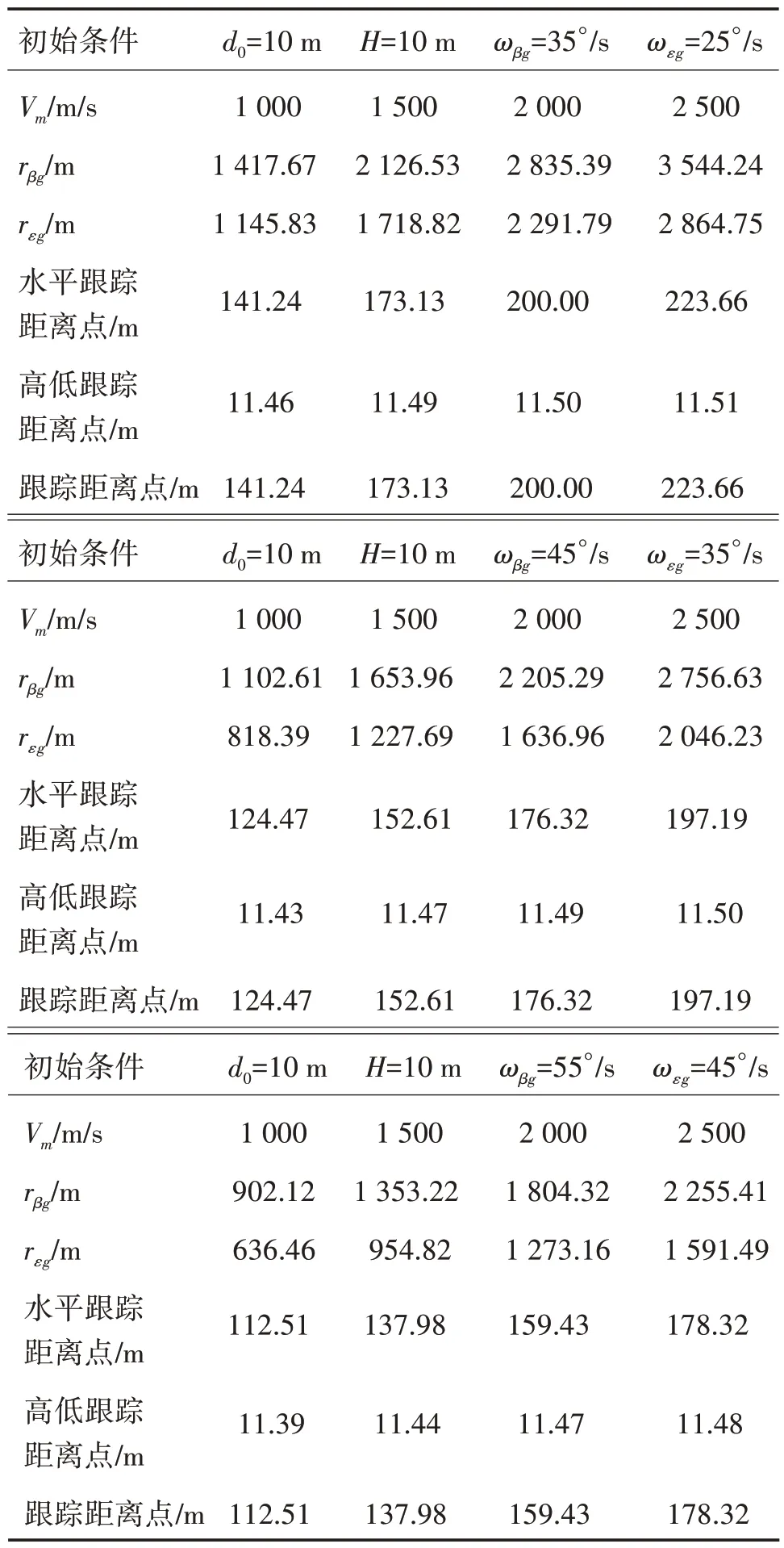
表1 本舰观测设备的跟踪死区Table 1 Tracking dead zone of warship observation equipment

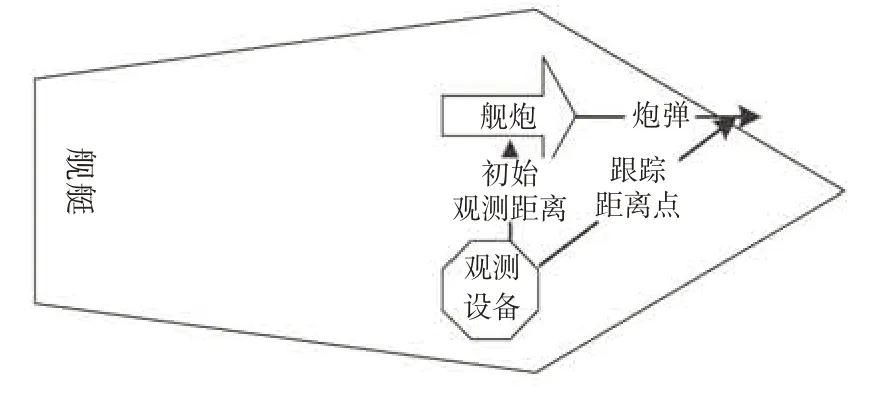
图8 本舰观测设备跟踪炮弹示意图Fig.8 Schematic diagram of tracking projectiles of warship observation equipment

通过上述仿真可以看出，当采用本舰观测设备对炮弹进行跟踪时，由于初始观测距离比较小，跟踪死区会一直存在，本舰传感器无法满足对出炮口炮弹的实时跟踪，随着炮弹初速的增大，死区半径也在增大，观测设备的跟踪距离点也在不断变大；观测设备跟踪角速度的增大，可有效减小跟踪死区的范围，当跟踪死区不可避免存在时，跟踪距离点可满足观测设备在该点处对炮弹的稳定跟踪。

3.2.2 协同平台观测设备跟踪

协同平台观测设备相对炮口的水平捷径较大，如下页图9所示，设初始观测距离d0稍大，观测设备最大方向跟踪角速度ωβg为35°∕s，最大高低跟踪角速度ωεg为25°∕s，炮管倾角φ=30°，炮弹飞行速度Vm为1 000 m∕s、1 500 m∕s、2 000 m∕s、2 500 m∕s 时进行仿真分析，结果如表2 所示。

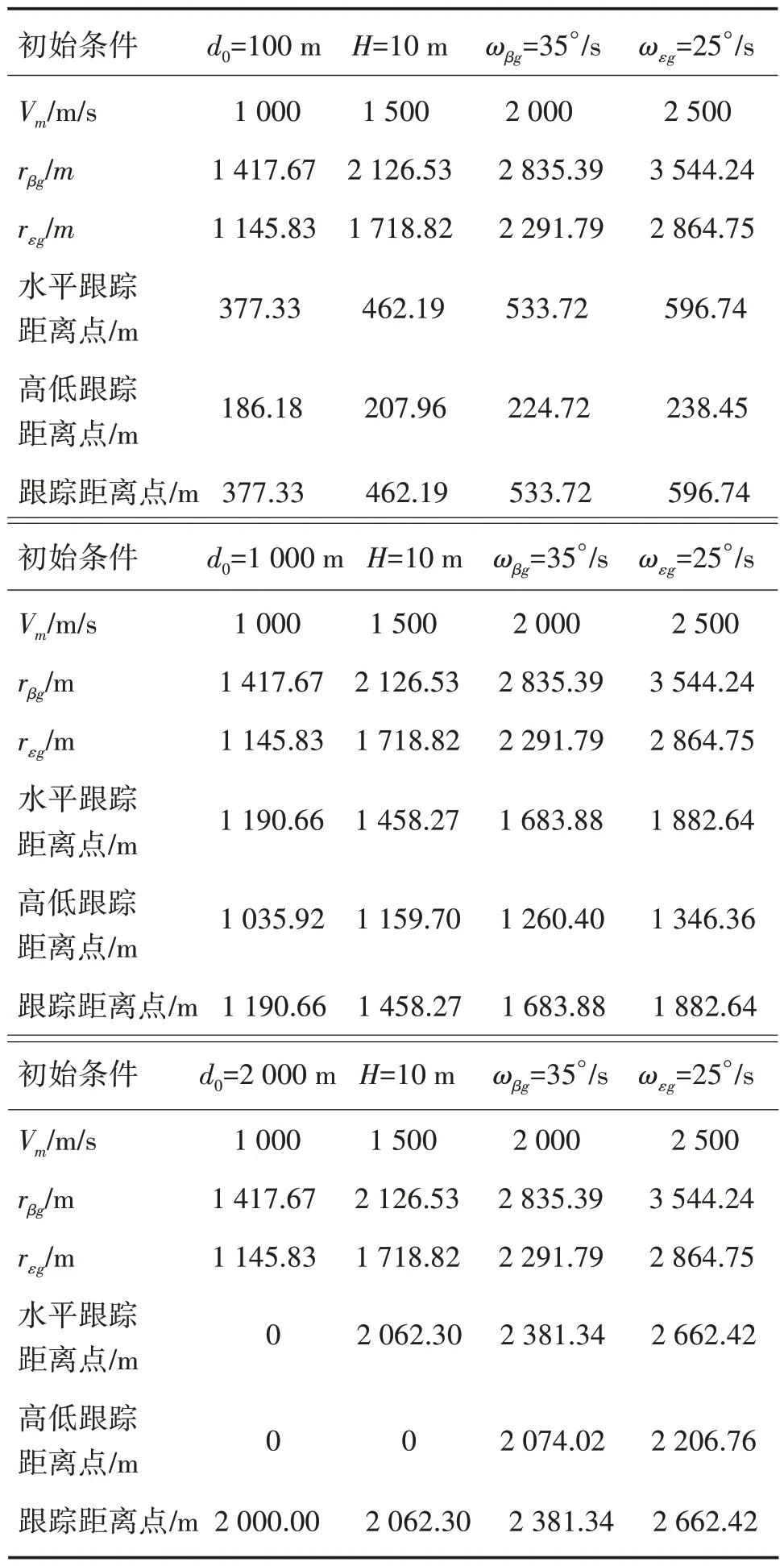
表2 编队观测设备的跟踪死区Table 2 Tracking dead zone of formation observation equipment

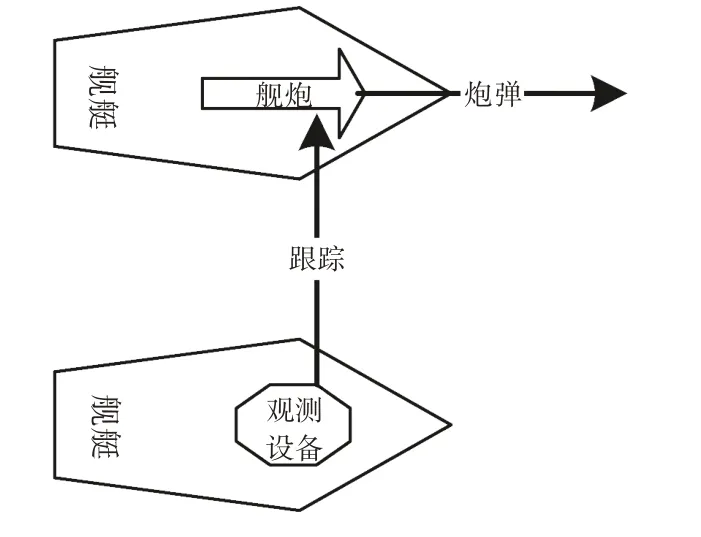
图9 编队观测设备跟踪炮弹示意图Fig.9 Schematic diagram of tracking projectiles of formation observation equipment

当采用编队观测设备对炮弹进行跟踪时，由于初始观测距离比较大，此时会存在跟踪死区，跟踪死区随着炮弹速度的增大而增大，在其航路上设置相应的跟踪距离点，实现对炮弹的稳定跟踪；当初始观测距离足够大时（如d0=2 000 m），可以看到当炮弹速度较小时，跟踪死区为0，说明此时观测设备不存在跟踪死区，在观测设备的观测精度范围内，采用编队观测设备跟踪炮弹，即获得了较大的初始观测距离，会有更大可能实现对炮弹的全程跟踪。

4 结论

本文针对新型舰炮武器炮弹初速大，对跟踪角速度要求高的特点，结合观测设备和炮弹的各项性能指标，建立观测设备对炮弹方向和高低跟踪死区模型。通过模型仿真分析方向、高低跟踪死区半径与炮弹速度和观测设备最大跟踪角速度之间的关系。通过仿真分析可知，跟踪死区受初始观测距离影响较大；跟踪死区大小与炮弹速度成正比、与观测设备跟踪角速度成反比；当炮弹速度较小，本舰观测设备性能较好，可采用本舰观测设备进行跟踪；当炮弹速度较大，或者不可避免产生跟踪死区时，一方面可采用编队观测设备进行跟踪，另一方面可根据计算得到的跟踪距离点，为跟踪炮弹做好准备。在实际应用过程中，可依据本文仿真结果，结合具体条件进行调整，实现对初速可调舰炮炮弹的有效跟踪。