基于飞行时间差的异构反舰导弹任务分配研究
2024-04-27邹智伟尹肖云姬文苏
邹智伟,邹 强*,尹肖云,姬文苏,2
(1.海军工程大学兵器工程学院,武汉 430033;2.陆军工程大学军械士官学校,武汉 430075)
0 引言
现代舰载防御能力较强,依靠单枚导弹打击目标舰艇难度大、代价高,集群协同作战成为研究热点。当多枚导弹同时打击目标舰艇时,导弹拦截难度增大[1]。因此,导弹集群协同作战中,以导弹进袭时间差为基础的协同时间优势,是异构反舰导弹集群组网动态攻击任务分配的关键分配因素,进袭时间差越小,舰艇越难以拦截。
现有任务分配研究中,大多以离线预分配模型进行完成任务分配,并且在任务分配过程中,大多以飞行里程最小[2-4]、毁伤概率最大[5-7]等为优化目标。而在线任务分配研究中[8-14],大多以同构集群作为研究对象进行实时任务分配[8-12],且优化目标多以最大毁伤概率等因素来进行任务分配。而在实时任务分配问题中,面临复杂的攻防对抗环境,包括导弹集群打击时间差、导弹-目标距离、导弹飞行速度、信息对抗等因素,对集群协同作战要求较高,同构系统难以应对如此复杂的作战环境。而异构反舰导弹集群协同通过导弹导引头类型的多样性,能够有效提高导弹集群作战效能,提高集群系统的抗干扰能力。另外,在反舰导弹集群协同作战的任务分配中,根据反舰作战过程,可分为预攻击阶段、攻击阶段以及侦察与毁伤评估阶段。其中攻击阶段任务分配决定着战场态势走向,对整体作战影响较大。因此,异构反舰导弹集群的协同作战动态攻击任务分配研究具有较大的研究价值。
在异构反舰导弹集群动态任务分配研究中,若选择错误的优化目标,可能使得导弹集群穿过敌方作战阵地进行越舰攻击,从而造成导弹集群整体的毁伤效能降低。
针对异构反舰导弹集群协同作战实时攻击任务分配问题,通过建立基于时间协同的优势函数,和一种实时求解算法,寻求满足符合反舰导弹集群作战要求的分配方案,保证能够完成对距离较近、花费时间较短、打击紧迫性较高的目标打击任务。
1 任务分配问题描述
1.1 异构反舰导弹集群任务分配问题描述
假设我方现有不同类型反舰导弹n枚,现有m个敌方威胁目标。考虑到现有反舰导弹作战大多为掠海飞行弹道[15],导弹飞行高度过高容易使导弹被舰载防空系统击落,同时为降低模型计算复杂度,忽略导弹飞行高度,以二维平面模拟导弹集群作战空间。导弹飞行过程中速度不变,同时,结合敌方舰艇防御干扰策略[16]。根据上述模型,其二维作战示意图如图1所示。

图1 导弹作战二维态势图Fig.1 Two-dimensional situation diagram of missile operation
图1 中,Mi1,l表示我方第i1枚导弹其导引头类型为l1类型的导引头;Tj,k表示敌方第j个目标装备有第k类型的防御措施;Di1,j表示该导弹与目标弹目距离;Vi1表示第i1枚导弹飞行速度;Ri1,min、Ri1,max分别表示第i1枚导弹导引头探测距离的近界与远界。
在异构导弹集群反舰作战的过程中,结合导弹相关作战原则,需要将导弹进行合理的攻击任务分配,以保证弹群作战满足作战打击相关策略,同时提高导弹集群的协同性,更好地发挥导弹编队协同打击与抗干扰能力。
综上所述,本文研究异构导弹集群的反舰作战攻击分配问题,以导弹集群中导引头类型、导弹飞行速度以及导弹针对不同目标的毁伤概率,来体现集群的异构特性。
1.2 异构导弹集群反舰作战攻击分配原则
本文研究背景为导弹发射后的临机动态分配场景下的异构弹群组网攻击任务分配问题。该研究方向与导弹射前目标预分配不同,本文对分配模型的实时性要求较高,应综合考虑导弹集群在当前时刻的攻防对抗态势信息。在导弹导引头类型、飞行速度以及导弹针对目标毁伤概率确定的情况下,其攻防对抗态势主要包括:导弹针对各个目标的剩余飞行时间、协同攻击时间差、导弹与目标之间的弹目距离以及导引头与目标匹配信息。
1)导弹集群反舰作战时,根据“先见先打”“避实就虚”的作战原则,避免导弹穿越其他目标造成越舰攻击,导致导弹集群协同作战效率降低,决定优先攻击距离导弹集群剩余飞行时间较少的敌方目标。
2)针对目标舰载防御措施,为保证导弹制导精确,需保证分配给某一目标的导弹集群具有导引头对抗优势。因此,应在导弹集群中分配至少一枚导弹导引头能够对抗敌方舰载防御措施,保证集群后续打击过程的准确性。
3)导弹集群协同攻击同一目标时,根据导弹集群协同作战原则,到达时间差距越小,目标越难以拦截,集群协同优势越高。所以应尽量为任务分配到达时间差距较小(协同度最高)的导弹,以较少的导弹数量完成对单个目标的打击,保证整体毁伤效果的最大化。
4)对目标而言,除时间协同优势外,导弹的距离优势与速度优势对集群作战也有一定影响。因此,在时间协同优势相近的导弹中,优先分配距离优势较大的导弹,速度优势影响程度最小。
2 异构导弹集群目标优势函数与数学模型的建立
2.1 任务分配模型优势函数定义
在进行异构导弹集群的攻击任务分配时,因集群中作战信息复杂,为保证计算合理性,需将各项数据进行量化处理。
2.1.1 异构导弹集群作战信息量化
为量化分配原则以及后续编程仿真,构造以下矩阵描述导弹集群打击敌方目标的相关作战信息。
1)导弹-目标分配矩阵X:
其中,xnm取值范围为{0,1},xnm=1 表示将第n枚导弹分配给第m个目标;xnm=0 表示第n枚导弹没有分配给第m个目标。
2)导弹毁伤概率矩阵P:
其中,pnm表示第n枚导弹目标m的概率。假设该毁伤概率指在不考虑敌方干扰条件下,打击敌方目标的毁伤概率。为降低模型的计算复杂程度,本文毁伤概率的确定通过导弹自身作战性能以及以往作战数据信息,结合蒙特卡洛方法仿真得到[17],并设为已知条件。
3)各导引头与目标防御干扰措施对抗信息矩阵Y:
其中,ylk取值{0,1},ylk=1 表示第1 种类型的导引头针对第k种防御措施能够有效打击目标;ylk=0 表示第1种类型的导引头受到第k种防御措施干扰。
4)弹目距离矩阵D:
其中,Dnm表示第n枚导弹与第m个目标之间的弹目距离,该弹目距离根据导弹机动飞行轨迹,结合飞行速度误差,将导弹飞行过程近似为匀速飞行的直线打击过程。
2.1.2 导弹时间协同优势函数定义
根据式(4)中的弹目距离定义以及各导弹平均飞行速度Vi,则第i枚导弹对第j个目标的剩余飞行时间Tij=Dij∕Vi,剩余飞行时间矩阵T:
在此基础上,定义时间差距为:ΔTij=|Tij-TJ|其中,TJ为针对敌方第j个目标时,按照分配原则指定的第1枚导弹剩余飞行时间。
根据导弹集群作战中“时间差距越小,集群协同度越高,作战优势越大”[18-19]这一基本认识,定义导弹时间协同优势函数如下:
其中,maxΔTj=max{ΔT1j,ΔT2j,…,ΔTnj}弹集群针对第j个目标时间差距最大值。本文导弹集群主要以导弹剩余时间较少的目标优先打击,因此,时间优势函数以打击某一目标j时,分配到的第1枚导弹飞行时间为基准,计算剩余导弹与之时间差距。则针对敌方第j个目标构成异构导弹集群的时间协同优势矩阵STj:
2.1.3 导弹距离优势函数定义
根据上述中的相关假定条件,设导弹导引头探测范围为Rmin~Rmax,其中,Rmin、Rmax分别为导弹导引头的近界与远界。当弹-目距离d≫Rmax或d≪Rmin时,通过单枚导弹自身的搜索探测功能可能无法探测到目标信息,但是在导弹集群中,各个导弹通过组网通信交换作战信息,使得导弹集群中各个作战单位不会完全丢失目标。因此,认为距离优势较小,而不是为0;当d=(Rmin+Rmax)∕2 时,导弹的距离优势最大[20]。则根据上述作战想定,定义导弹的距离优势函数为:
其中,d0=(Rmin+Rmax)∕2;σD=Rmax-Rmin为导弹导引头探测距离范围决定的常量。上述距离优势函数既保证了目标在搜索范围内的相对优势,又体现了目标不在导弹搜索范围内时导弹的相对劣势。则sDij构成异构导弹集群的距离优势矩阵SD:
2.1.4 导弹速度优势函数定义
根据假设条件,即导弹由当前状态直至命中敌方目标过程中保持飞行速度不变。根据“导弹飞行速度越快,目标越难以拦截”这一基本认识,定义第i枚导弹速度优势函数为:
其中,Vi为第i枚导弹的飞行速度;Vmin=min{V1,V2,…,Vn},即导弹集群中导弹飞行速度最小值。该函数既保证了导弹飞行速度与相对优势的相关变化关系,又使速度优势数量级与时间协同优势和距离优势一致。
2.1.5 导弹集群导引头匹配优势矩阵
结合式(1)的目标分配矩阵X以及式(3)导引头与目标防御措施对抗信息矩阵Y,可确定导弹集群针对目标群的导引头匹配优势矩阵Z:
其中,zij=0 或1。zij=1,表示在无其他导弹协同的条件下,第i枚导弹对敌方第j个目标具有导引头对抗优势;zij=0,表示在无其他导弹协同的条件下,第i枚导弹对敌方第j个目标不具备导引头对抗优势。
2.2 任务分配模型优势数学模型建立
2.2.1 综合毁伤概率计算
根据2.1 节中式(2)定义的异构导弹集群的毁伤概率矩阵,计算导弹集群打击敌方第j个目标时,至少有1枚导弹毁伤目标的概率为:
2.2.2 任务分配约束条件与任务分配数学模型
根据反舰导弹作战性质,以及相关作战约束可得以下几点约束条件:
1)每一枚导弹只能分配给一个目标,即
2)保证集群针对每个目标的毁伤概率达到一定的阈值:
其中,P0为导弹集群攻击毁伤概率阈值,当针对目标的毁伤概率大于该阈值时,则认为我方导弹集群可以完成对该目标的打击任务。
3)导弹集群分配目标方案时,保证方案中至少有1枚导弹具有导引头匹配优势:
3 异构反舰导弹集群任务分配
在分配过程中,结合2.2 节中任务分配原则,根据导弹集群中剩余飞行时间确定集群首要打击目标,再根据其他导弹剩余飞行时间协同优势、弹-目距离优势、飞行速度优势等因素逐个分配导弹,直至满足作战毁伤预置要求,再对下一目标进行导弹分配,得到一个基于时间协同的分配方案,具体分配步骤如下。
1)根据导弹集群的剩余飞行时间矩阵T,选择目标。定义
则从目标1~m中选择待分配的第J1个目标,当且仅当
即导弹集群剩余飞行时间之和最小的作为优先打击目标。
2)为目标J分配第1 枚导弹。根据导弹集群剩余飞行时间矩阵T与导引头匹配优势矩阵Z,按以下原则选择分配给目标J的第1枚导弹:在满足导弹导引头匹配优势的导弹中,剩余飞行时间最小的优先分配。
即当且仅当
时,令xI1J=1;xIj=0,j≠J。
同时根据TJ计算导弹集群针对第J个目标的时间协同优势矩阵STJ。 根据导弹毁伤概率pI1J, 当pI1J不能满足式(15)时,则继续为目标J分配导弹。
3)为敌方第J个目标分配第2 枚导弹。根据时间优势矩阵STJ、距离优势矩阵SD、速度优势矩阵SV,为目标J分配原则为:首先根据指定的第1枚编号为I导弹,优先分配使时间协同优势较大的导弹;时间优势相同时,距离优势较大的导弹优先分配;速度优势较大优先分配。
定义
其中,c1、c2、c3∈(0,1),且c1+c2+c3=1。
式(20)由3 个部分组成,时间协同优势STiJ、距离优势、速度优势。在任务分配决策中,本文主要目的是以时间协同优化为主,因此,时间协同优势优先于其他两个优势,在式(19)中主要体现在c1的取值上,则0.5 ≤c1<1。除时间协同优势外,导弹的距离优势和速度优势对导弹集群的攻击任务分配也有一定的影响,其影响程度由c2、c3的取值决定。同时根据分配原则,c2>c3。具体数值可根据专家经验给出。
则将第I2导弹分配给第J个目标的充分必要条件为:
并令xI2J=1;xI2j=0,j≠J。
4)计算协同突防概率。根据已分配给第J个目标的导弹,以式(12)计算综合毁伤概率,并判断是否满足式(15)的约束条件,若不满足,则转入步骤5);否则,转入步骤6)。
5)继续为目标分配可用导弹,直至满足式(15)的约束条件或者n枚导弹全部分配完毕。
6)针对剩余导弹以及剩余目标,重新选择待分配目标。此时定义
其中,Ik为已经分配的导弹编号。从剩余目标中选择第J2个目标,当且仅当
7)对第2个打击目标分配导弹。按照步骤2)选择打击目标J2的第1枚导弹,若剩余导弹集群中能够满足导弹导引头匹配优势,则继续按步骤3)~步骤5)继续分配导弹;若剩余导弹集群中无导引头匹配优势的导弹,则视为针对目标J2的打击任务无法完成,将该目标视为分配完成,跳转至步骤6)直至完成对所有目标的分配。
4 仿真设计与分析
4.1 仿真环境与初始条件
仿真环境:运行环境为Win10,CPU 为Intel(R)Core(TM)i5-7200U@2.50 GHz(4 CPUs),~2.7 GHz,内存8 G;仿真软件为Matlab 2020a。
初始条件:假设我方反舰导弹集群现有导弹数量n=8,目标舰艇数量m=3。根据集群中导弹飞行速度类型以及以往作战信息,设置c1=0.6,c2=0.3,c3=0.1,毁伤阈值P0=0.95。
则导弹集群作战初始位置以及导引头参数信息如表1所示。
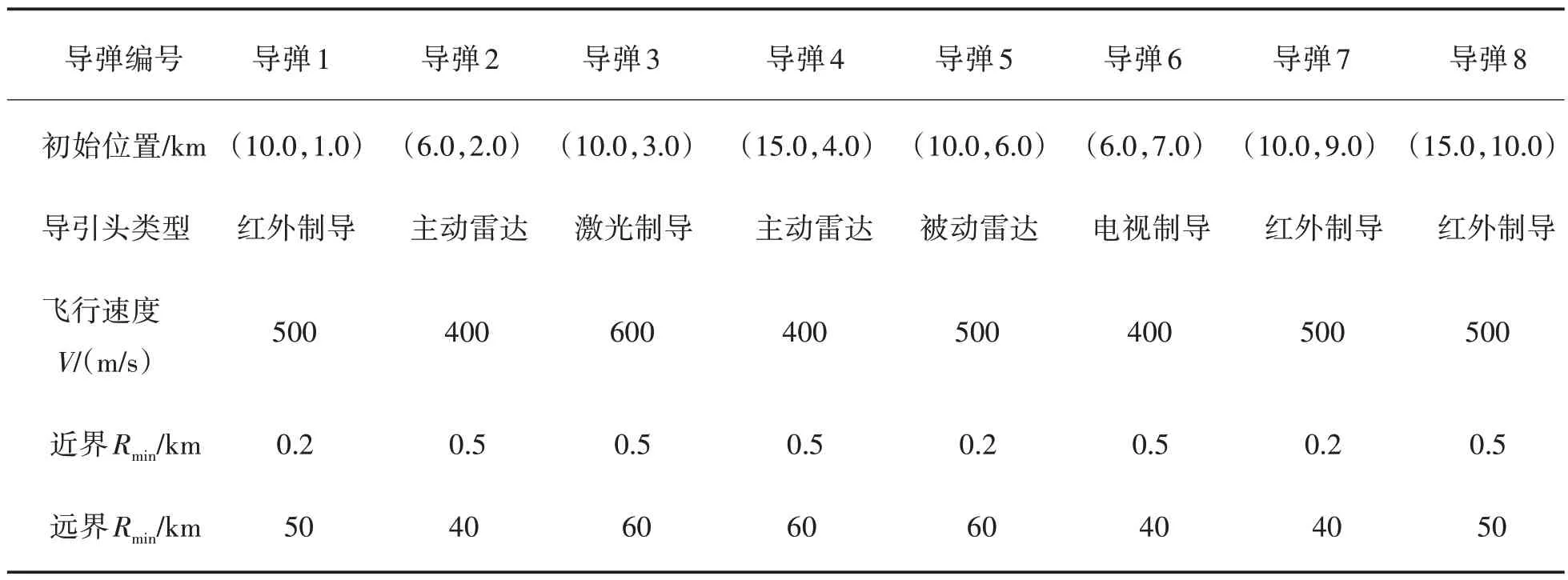
表1 导弹初始信息表Table 1 Initial missile information table
目标舰艇相关作战信息如表2所示。
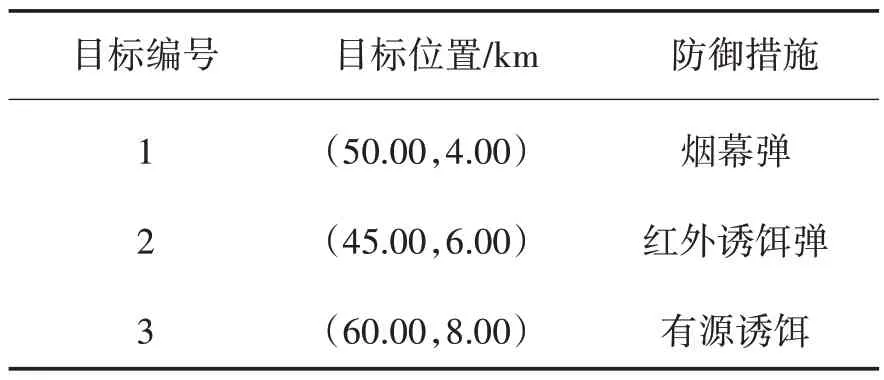
表2 目标位置信息Table 2 Target location information
反舰导弹毁伤概率如表3所示。

表3 反舰导弹毁伤概率Table 3 Damage probability of anti-ship missile
敌方舰艇常见防御对抗措施及对象如表4所示。

表4 导弹作战信息表Table 4 Missile operational information table
在实验仿真过程中,按照上述表格数据进行仿真获得分配方案。
4.2 仿真与分析
根据建立的异构弹箭导弹集群攻击任务分配方法,以及4.1节中设定的仿真初始数据,利用matlab 2020a,进行仿真。其结果与分析如下。
仿真结果如表5所示。

表5 导弹集群任务分配方案Table 5 Missile cluster task allocation scheme
根据异构反舰导弹集群攻击任务分配原则,得到导弹集群的打击顺序为目标2,目标1,目标3。得到分配矩阵X:
针对目标2,其分配导弹1 与导弹8 进行攻击任务,两枚导弹飞行时间分别为58.54 s、60.5 s,最大时间差为1.96 s,查阅表4,该方案满足导引头匹配原则,其综合毁伤概率为0.971 1>P0。
针对目标1,其分配导弹5、导弹1与导弹7进行攻击任务,3 枚导弹飞行时间分别为70.0 s、70.77 s、70.25 s,最大时间差为0.77 s,查阅表4,该方案满足导引头分配原则,其综合毁伤概率为0.985 3>P0。
针对目标3,其分配导弹4、导弹6与导弹2进行攻击任务,3 枚导弹飞行时间分别为112.94 s、135.02 s、135.83 s,最大时间差为22.83 s,查阅表4,该方案满足导引头分配原则,并计算其综合毁伤概率为0.990 5>P0。
带有时间协同优势的目标分配算例表明:针对时间紧迫性较高的目标,在保证满足预期毁伤概率的基础上,能够较好地满足时间协同策略,保证我方导弹集群协同打击目标的进袭时间差最小,提升了弹群突防优势,符合战场实际。同时该模型的计算分配时间为0.087 s,满足在线攻击任务分配的时间要求。仿真结果证明了本文提出的异构反舰导弹集群攻击任务分配模型的有效性。
5 结论
针对海上反舰作战的异构导弹集群时间协同任务分配问题进行了一定的探索性研究。首先针对异构反舰导弹集群攻击任务分配问题,根据当前交战情况下的弹目态势信息,提出了基于导弹飞行时间差的时间协同优势,并在已有研究基础上,改进了导弹距离与速度优势。在异构导弹导引头匹配约束以及其他作战约束条件下,建立了一种在线实时分配方法。最后通过仿真案例分析,取得了满意的分配结果,验证了模型与分配方法的有效性。
同时,本文在某些方面仍存在不足,一方面,如在目标携带防御措施种类上,只假设目标携带一种防御措施,导弹剩余飞行时间利用近似飞行轨迹估算,不够精确等问题。另一方面,在更复杂的目标舰队作战环境下,导弹轨迹规划与剩余飞行时间精确的计算是下一步研究工作。
