火炮远方瞄准点法误差分析研究

韩 超，闫媛媛，刘广生，段纬然，刘 亮

（陆军工程大学石家庄校区，石家庄 050003）

0 引言

火炮在射击时，为了命中目标，必须使火炮发射炮弹的平均弹道通过目标［1］。要使火炮发射炮弹的平均弹道通过目标，发射前必须操纵火炮，使其炮身轴线在空间处在平均弹道通过目标的位置上。操纵火炮使其炮身轴线在发射前处在这一特定空间位置的过程，称为火炮的射击瞄准［2-4］。大口径压制火炮区别于坦克，其主用瞄准方式为间接瞄准，是指在瞄准过程中，借助于特别选定的瞄准点作为辅助目标来进行瞄准。在间接瞄准时，瞄准手只要看到瞄准点（标定点），而无需看到要射击的目标。一般火炮阵地与目标之间距离较远，目标不能直接看见时，采用间接瞄准法［5］。

瞄准时，火炮炮身轴线在空间的位置可由两个角度数值确定：方向角和高低角。因此，按照火炮瞄准的操纵过程，瞄准又可分为：

1）方向瞄准：使炮身轴线在水平面内指向一确定的方向，方向瞄准也称水平瞄准；

2）高低瞄准：使炮身轴线在垂直面内处于一定的俯仰角，高低瞄准也称垂直瞄准。

1 方向瞄准

方向瞄准使炮身轴线在水平面内指向一定的方向。方向瞄准需要周视瞄准镜与方向机配合完成，周视瞄准镜简称周视镜或周瞄镜，是一种可用于360°环形观察［6］，并与方向机配合供火炮方向瞄准的潜望类瞄准镜，方向机为炮塔的转动驱动装置。

方向瞄准流程分3步，以远方瞄准点法为例：

1）利用自然地物作为瞄准点（标定点）进行间接瞄准。火炮基准射向被赋予后，对基准射向进行标定［7］。瞄准手通过转动周视瞄准镜的方向和俯仰转轮，使目镜中的分划板立标对准标定点，如图1所示，图中实线为周瞄镜向标定点标定时的瞄准线。

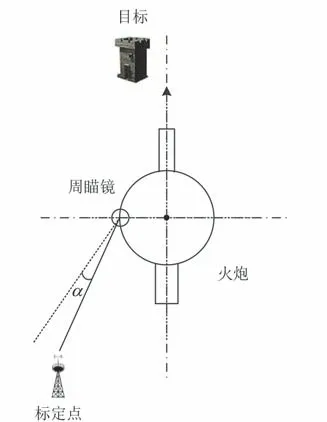
图1 远方瞄准点法示意图（a）Fig.1 Schematic diagram of remote aiming point method（a）

2）瞄准手通过转动方向手轮在周瞄镜上装定方向角。在装定完方向角后，目镜中的分划板立标偏离标定点，原来对准标定点后的瞄准线偏离标定点所装定的方向角，如图1中的虚线所示。

3）瞄准手一边观察周瞄镜的目镜，一边转动方向机，使周瞄镜分划板立标重新对准标定点，完成方向瞄准，如图2所示。对于方向瞄准而言，如果存在瞄准误差，随着射击距离的增加，射弹在方向上将离目标越来越远，射击距离对方向上的瞄准误差具有放大作用，一般瞄准误差过大，很可能使射弹超出安全区，造成安全事故。

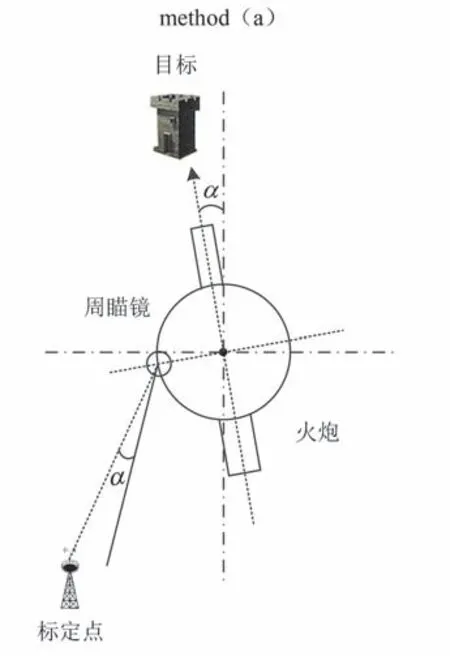
图2 远方瞄准点法示意图（b）Fig.2 Schematic diagram of remote aiming point method（b）

2 几何模型建立

从上述方向瞄准过程可知，由于周瞄镜与火炮回转中心有约0.4 m 的横向距离偏差，使得周瞄镜转动中心与火炮回转中心不重合，这个偏差会导致火炮方向瞄准时带来瞄准误差，直接影响火炮的射击精度［8］。标定点应该选择在多少米之外能够满足所要求的瞄准误差，标定点应该选择在火炮的左前、左后、右后还是右前才能够满足所要求的瞄准误差，这些问题鲜有文献研究。

图3 中，O为火炮的回转中心，O1为周瞄镜的转动中心，e为周瞄镜与火炮回转中心之间的偏心距，e=OO1，T为标定点，O1T=L为周瞄镜与标定点之间的距离，简称标定点距离。瞄准线O1T与横轴正向的角度为γ，用于表示标定点位置。当射向需要改变α角时，首先需要在周瞄镜上装定α角度，此时周瞄镜偏离了标定点T。然后转动火炮方向机，直至周瞄镜重新瞄向T。由于周瞄镜与火炮回转中心有一偏心距e，周瞄镜随火炮转动β角才能瞄准标定点T，α与β不相等从而产生方向瞄准误差。图3 中，O'1坐标为O'1(-ecosβ，-esinβ)，火炮转动β角后，O'1T斜率为K=tan(π-γ-a+β)，过O'1且斜率为K的直线方程如下：

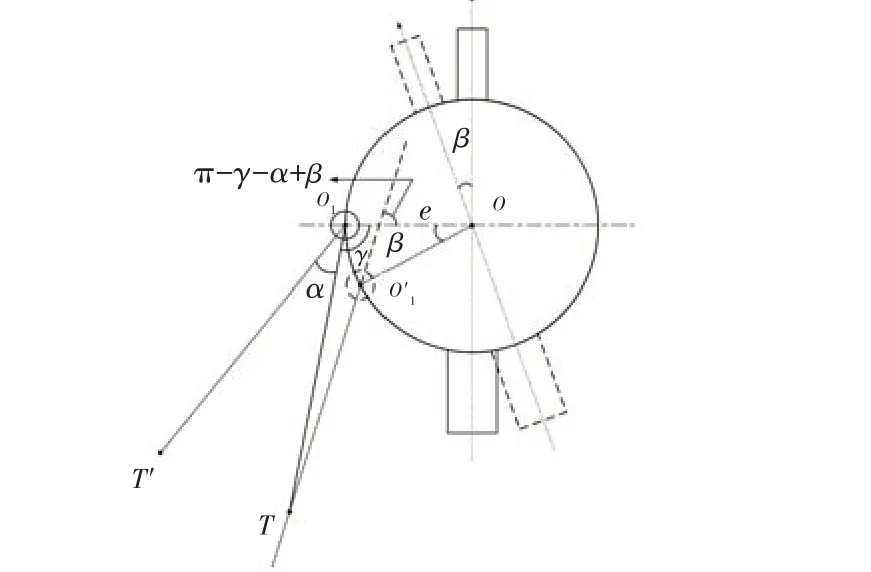
图3 标定点位于左后方瞄准示意图Fig.3 Schematic diagram of the calibration point located at the left and rear aiming

如图4 所示，O'1坐标为O'1（-ecosβ,-esinβ），火炮转动β角后，O'1T斜率为K=tan(β-γ-α)，过O'1且斜率为K的直线方程如下：

图4 标定点位于右后方瞄准示意图Fig.4 Schematic diagram of the calibration point located at the right rear aiming

式（2）和式（4）通过换算是等价的。火炮装定的方向角为α，火炮实际转动的角度为β，a-β为赋予火炮方向角时所带来的误差。将式（4）进行转换，将火炮实际转动角度β与装定角度a、标定点距离L和标定点位置γ之间的函数关系转换为显性函数，步骤如下：

将式（7）两边同时乘以cosβ，得下式：

从上式可知，通过转换后，火炮实际转动角度β与装定角度α、标定点距离L和标定点位置γ之间的隐性函数转换为显性函数，但函数关系式较为复杂，无法直观地看出各个参数之间的相互关系。

3 瞄准误差分析

3.1 标定点位置关系与瞄准误差关系

根据火炮瞄准实际，从以下几个方面分析瞄准误差的变化情况：1）将标定点位置固定，改变装定的方向角，分析归纳装定的方向角大小与瞄准误差之间的关系；2）改变标定点的位置，分析归纳标定点的位置与瞄准误差之间的关系；3）改变标定点距离，分析归纳标定点距离与瞄准误差之间的关系。

火炮瞄准时，标定点位置选择可分布于火炮左前、左后、右前和右后。如下页图5 所示，在装定角度不变的情况下，改变标定点的位置，从左后方到左前方每隔10°选择一个标定点。从右前方至右后方每隔10°选择一个标定点。并将标定点距离划分为100 m、200 m、300 m、400 m 和500 m，通过编程计算可得瞄准误差曲线如图6、图7所示。

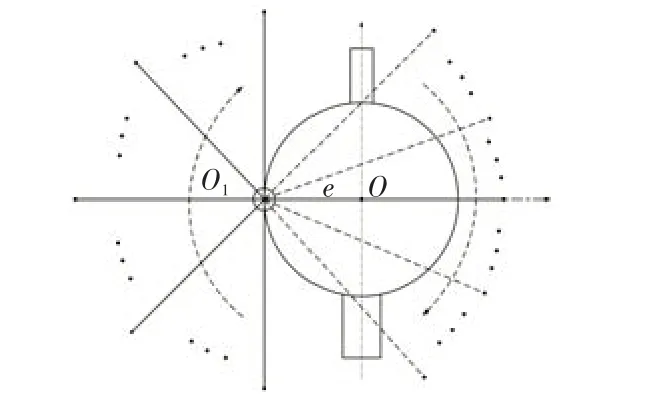
图5 标定点位置变化示意图Fig.5 Schematic diagram of the change in the position of the calibration point

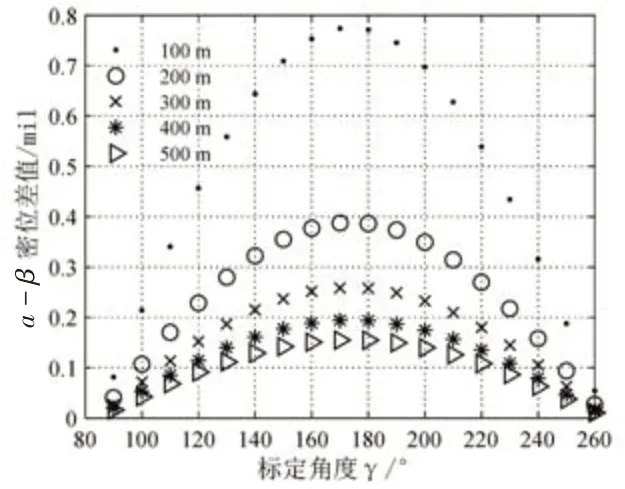
图6 改标定点方向误差曲线（左后到左前）Fig.6 Change the direction error curve of the calibration point（from left rear to left front）

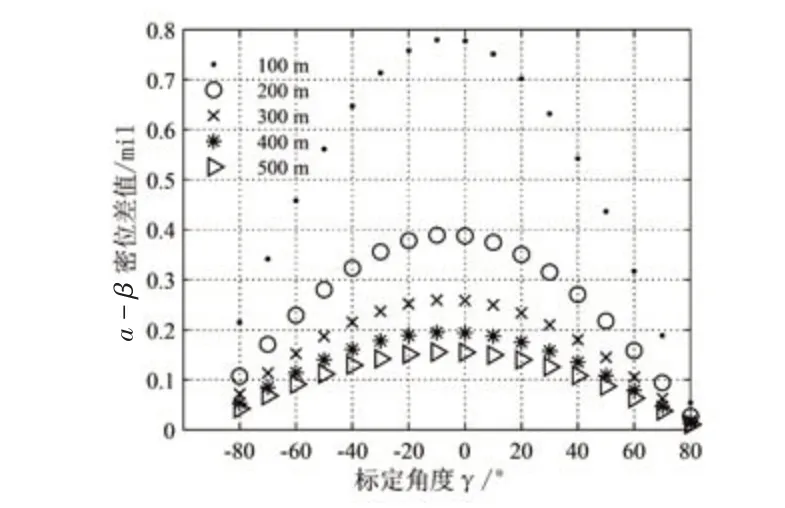
图7 改标定点方向误差曲线（右后到右前）Fig.7 Change the direction error curve of the calibration point（from right rear to right front)

从图中可看出，当标定点距离确定后，随着标定点位置的变化，瞄准误差点的分布均呈现出两边低中间高的特点。其中，瞄准误差较大的点对应的是火炮的正左侧和正右侧的标定点。标定点越靠近正前或者正后，瞄准误差越小。同时，通过观察瞄准误差曲线可知，当装定角度固定后，随着标定点距离的增加，瞄准误差会减小。当标定点距离较小时，标定点距离的变化会导致瞄准误差变化较大。当标定点距离大到一定程度后，标定点距离变化时，瞄准误差变化较小，这也说明标定点距离大到一定程度后，可以削弱标定点位置选择不佳所带来的瞄准误差。

3.2 标定点距离和装定角度与瞄准误差关系

从上述标定点位置关系与瞄准误差关系分析可知，标定点位置选择在左半部分还是右半部分，其瞄准误差变化规律基本一致。因此，选择左后方标定点进行标定点距离和装定角度与瞄准误差关系分析。将装定角度设置为0°～50°，并均分为100个数据点。标定点距离设置100～500 m，并均分为100 个数据点。标定的位置选择与横轴正向成100°、110°、120°、130°、140°、150°，共6 个角度，使用MATLAB mesh函数生成三维图形［9］。

如图8 所示，图中x、y、z分别表示标定点距离、装定角度和瞄准误差。从图（a）～图（f）6个三维图形可知，标定点距离越小、装定角度越大均会造成较大的瞄准误差，反之，瞄准误差减小。图中6个三维图的形状特征基本一致，说明标定点的位置选择，不会影响标定点距离、装定角度与瞄准误差之间的定性关系。标定点位置越靠近横轴左右两侧，瞄准误差越大。

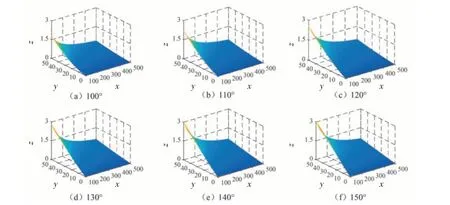
图8 标定点距离和装定角度与瞄准误差关系Fig.8 The error relationship between the distance and setting angle of the calibration point and the aiming error

3.3 瞄准误差极值

将标定点距离划分为100 m、200 m、300 m、400 m和500 m，装定角度从5°～50°，间隔5°。改变标定点的位置，从左后方到左前方每隔10°选择一个标定点，并计算瞄准误差。计算每一个标定点距离和装定角度下的瞄准误差极值如表1 所示。使用MATLAB cftool 工具箱中的多项式函数对表1 数据进行多项式拟合［10］。分别设定装定角度和标定点距离的最高幂次为1～4，使用和方差SSE、确定系数Rsquare、调整确定系数Adjusted R-square 和均方根误差RMSE表征拟合多项式函数的拟合效果，如表2所示，从表数据中可知，增加L的幂次对于降低拟合误差更有效。考虑到拟合效果和多项式的复杂程度，选择L多项式幂次为4，α多项式幂次为1，对应多项式如下：

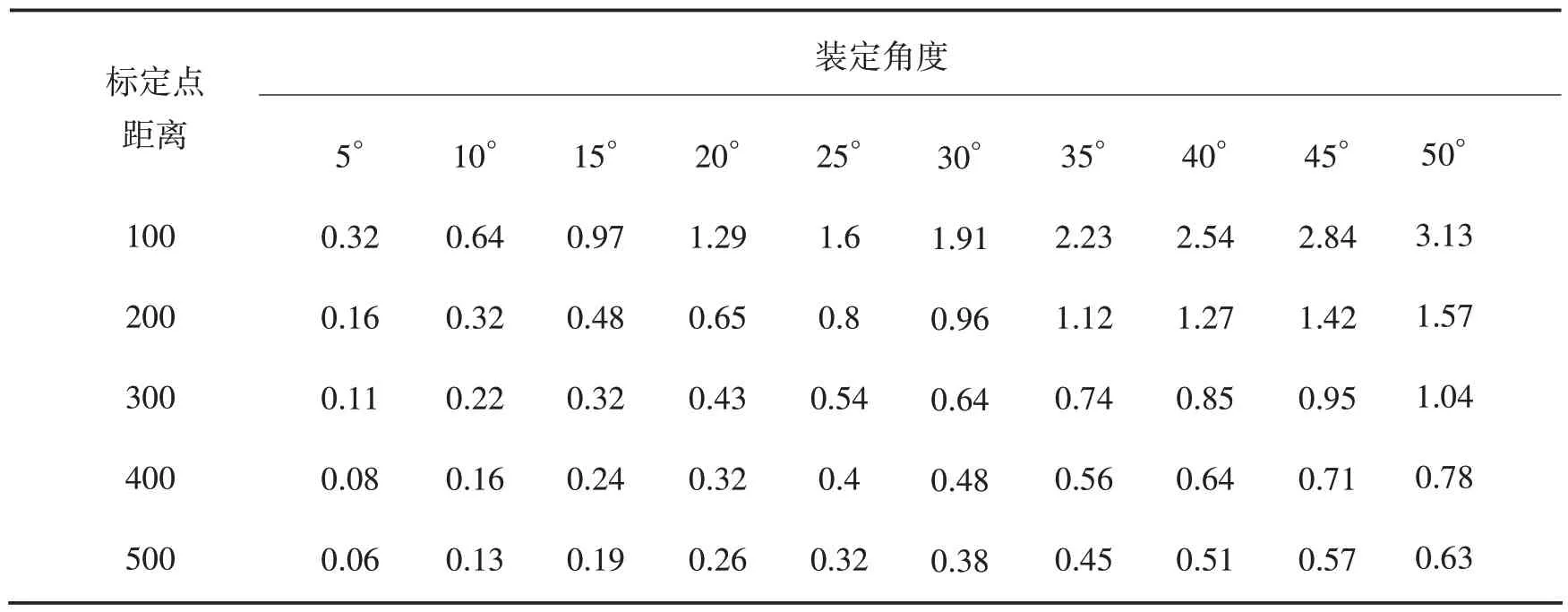
表1 瞄准误差极值∕milTable 1 Extreme values of aiming error∕mil

表2 多项式拟合结果Table 2 Fitting results of polynomial

4 标定点设置建议

由上述瞄准误差分析可知，装定角度、标定点距离和标定的位置均与瞄准误差有关。在标定点位置和标定距离确定后，装定角度不易过大，否则会带来较大的瞄准误差。标定点的位置应尽可能靠近火炮前、后两侧，越靠近左、右两侧也会带来较大的瞄准误差。所以，一般从左前至后来寻找合适的物体作为标定点。从理论分析的角度，选择右后侧和右前侧也不会带来太大的瞄准误差，但是由于自行火炮炮塔结构问题，选择右方标定点易产生视线遮挡，一般不选择右侧标定点。无论何种情况下，增大标定点距离都会减小瞄准误差，所以在能看清标定点的前提下，应尽量选择较远的物体作为标定点，以减小瞄准误差。

5 结论

本文对方向瞄准方法中的远方瞄准点法进行了几何建模，通过几何模型对周视瞄准镜与火炮回转中心不同心所造成的瞄准误差进行了公式推导。采用数值计算方法获取了多组标定点距离、装定角度、标定点位置和瞄准误差数据，通过绘制和分析图形得到减小瞄准误差的有效方法如下：1）装定角度不应过大；2）标定点位置应从左前至左后选择，同时应靠近前、后两侧；3）应尽可能增大标定点距离。同时，给出了装定角度、标定距离和瞄准误差极值之间的多项式拟合关系式，方便快速计算瞄准误差，供相关人员使用。