弹簧振子隔离器模型动态刚度特性试验及仿真研究

秦晓猛，刘天彦，牟浩文，宁薇薇

（1.天津航天瑞莱科技有限公司成都分部，成都 610100； 2.中国核动力研究设计院，成都 610213）

引言

受海浪或海风等海洋环境影响，舰船产生低频的激励，这些低频信号会对舰船上的设备产生影响；另一方面由于受到炮击，一些高频冲击信号也会对舰船上的设备产生损伤[1]。故而在地面试验中，常常需要对舰船设备进行冲击试验，以考核和验证装备在冲击条件下的工作适应性和结构完好性，以此来评价装备的抗冲击能力和水平[2]。为了减缓冲击损伤，隔离器广泛应用于舰船设备中，如动力设备、大型电柜和重型精密仪器等都带有各类型的隔离器。当前，在美国、俄罗斯和欧洲等国，舰船上都是安装有许多隔离振动减缓冲击的元件[3,4]。为了评价隔离器的隔离振动和抗冲击能力，需要准确了解其动态性能参数，隔离器的动态刚度特性包括动刚度和冲击刚度，这两项指标是隔离器性能评估的核心技术指标。

1 动态刚度物理模型与测试理论

当前，隔离器在实际的使用过程中，虽多组并联使用，其核心为基于单自由度系统模型。无论隔离器的型式如何变化，不同隔离器产品对应的测试方法也较多，但是都源于“激励→传递→响应”这一基础原理。根据不同的隔离器载荷、型式和试验设备，所采用的测试方法也存在一定差异。动刚度测试，主要采用的方法有振动激励法、自激振荡法和椭圆法；冲击刚度测试，主要采用的方法有跌落法和落锤法[5]。本文基于弹簧振子隔离器模型，采用振动激励法进行动刚度测试分析，采用跌落法进行冲击刚度测试分析。

1.1 动力学物理模型

根据单自由度弹性系统中惯性力、弹性力、阻尼力及外力平衡原理可以确定隔离器动态性能参数。当系统假定为结构阻尼、刚度为线性复刚度及输入为简谐力，在刚性基础情况下，M-K 弹性系统运动方程式为[6]：

式中：

—系统中隔离器的承重体（kg）；

K—隔离器动刚度（N/m）；

η—隔离器结构阻尼的损耗因子；

X—承重体的绝对位移（m）；

F0—激振力幅值（N）；

ω—激振圆频率（rad/s）。

1.2 振动激励法动刚度测试机理

当式（1）中F0=0、台面位移为u=u0ejωt时为基础激励，力学模型如图3 所示，运动方程式转化为：

求解方程（2），得到振动台激励的每个频率绝对位移响应幅值X0及绝对位移共振幅值X0max分别由公式（3）和公式（4）表示。

求解该运动方程式（5），得到振动台激励的每个频率相对位移响应幅值0δ及相对位移共振幅值δ0max分别由式（6）和式（7）表示。

式中：

u0—为振动台激振位移幅值（m）；

δ0—隔离器承重体M 相对台面位移幅值（m），

ωn—隔离器系统的共振频率（rad/s）。

M-K 弹性系统共振时，此时的激振力等于阻尼力，惯性力等于弹性力，动刚度可以按照式（8）计算：

1.3 跌落法冲击刚度理论

不同于动刚度，冲击刚度的冲击输入的脉宽通常远小于隔离器的自由振动周期，隔离器最大位移及最大传递力均发生在脉冲作用时间以内的时刻。图5 表征了冲击刚度的响应特征，t0时刻为隔离器上承重体响应加速度达到最大值的时刻，冲击刚度为瞬态过程，选择t0时刻之前隔振器的恢复力-变形关系来拟合冲击刚度。

基于跌落法的冲击刚度力平衡方程式为：

对式（10）进行积分，并整理简化后得到位移响应，即隔

式中：

Xch—隔离器承重体相对台面的位移（m）；

Kch—隔离器的冲击刚度（N/m）；

ηch—隔离器的冲击损耗因子；

um—试验台面的绝对冲击加速度（m/s2）；

τ—脉冲作用时间（s）；

M—系统质量（kg）。

1.4 跌落法冲击刚度测试机理

曲线横坐标为试验系统隔离器冲击变形瞬态测试值，纵坐标为试验系统传递力瞬态测试值。由于冲击大变形引起的非线性和冲击响应过程呈自振衰减状态，故冲击传递力-变形迟滞回线如图7 所示，呈现不对称性，图中最大冲击位移Xch点对应的力为最大冲击弹性力Ft，Fm为最大传递力[5]。

根据冲击刚度的定义，位移最大时刻对应的传递力为弹性力，冲击刚度由式（12）表示：

当系统冲击输入由台面产生时，即为跌落式冲击时，最大传递力按照式（13）计算：

式中：

Xch—最大冲击位移（m）；

Ft—最大冲击位移时对应的传递力（N）；

Fm—最大冲击传递力（N）。

2 动态刚度特性试验测试分析

为了探究隔离器的动态刚度特性，设计了一个弹簧振子隔离器模型，以验证动态刚度特性理论。采用振动台基于振动激励法对其进行动刚度测试，其测试状态如图8 所示。采用气动冲击台基于跌落法对其进行冲击刚度测试，其测试状态如图9 所示。弹簧振子配重10 kg。

2.1 动刚度测试程序及试验结果

采用振动激励法进行动刚度测试，将弹簧振子隔离器模型放置于振动台上，施加恒定加速度激励。弹簧振子隔离器模型顶部加速度与台面激励加速度的比值，形成的传递率曲线如图10 所示。

图1 隔离器

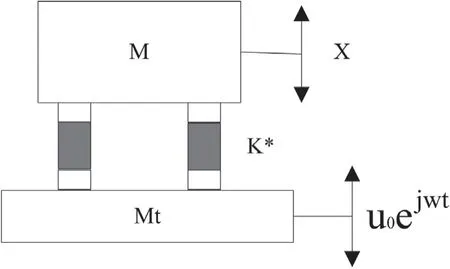
图3 激振扫描法力学模型

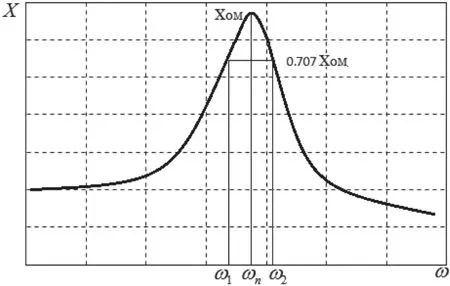
图4 传递力—位移迟滞曲线

图5 冲击瞬态时刻的输入和响应加速度曲线

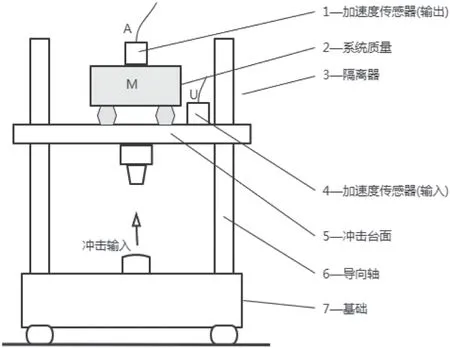
图6 冲击刚度测试系统（跌落式）

图7 冲击刚度迟滞回线

图8 振动激励法动刚度测试布置图

图9 跌落法冲击刚度测试布置图

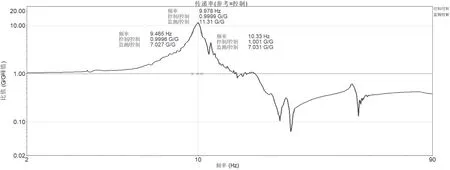
图10 振动激励法动刚度传递率曲线

根据弹簧振子隔离器模型的配重为10 kg，振动激励法形成的传递曲线可以看出共振频率为9.978 Hz。通过计算其动刚度Kd 为3.930 4*104N/m。

2.2 冲击刚度测试

跌落法冲击刚度测试是利用冲击试验机进行半正弦冲击，通过测量冲击过程中隔离器传递力及变形时域波形，求解隔离器的动态参数。根据GB/T 15168 中的冲击刚度测试方法和数据分析处理。该弹簧振子隔离器模型在跌落速度为4.7 m/s 的测试曲线如图11~14 所示，不同速度下跌落法冲击刚度测试结果见表1。

表1 跌落法冲击刚度测试结果

图11 加速度时域曲线(灰色输出、黑色输入)

图12 速度曲线(灰色输出、黑色输入)

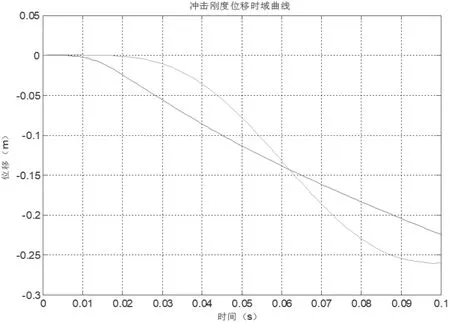
图13 位移曲线(灰色输出、黑色输入)

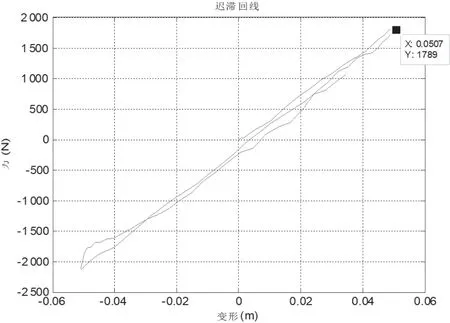
图14 迟滞回线(跌落速度4.7 m/s)

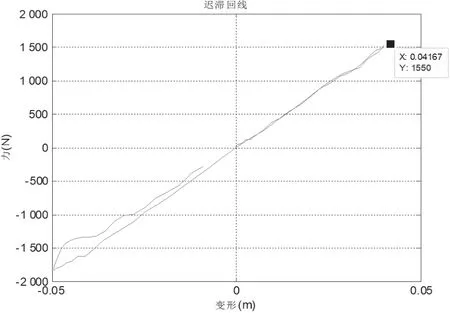
图15 迟滞回线(跌落速度4.2 m/s)

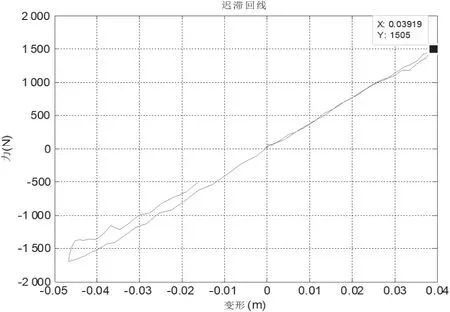
图16 迟滞回线(跌落速度3.9 m/s)

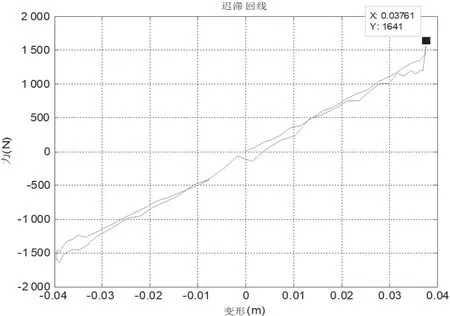
图17 冲迟滞回线(跌落速度3.6 m/s)

图18 迟滞回线(跌落速度3.4 m/s)

对不同跌落速度下的冲击刚度进行测试，获取不同跌落速度下的冲击刚度迟滞回线，求解对应的冲击刚度。可以看出冲击刚度在不同的冲击速度下存在差异，且该弹簧振子系统随着冲击速度的增加，而冲击刚度随之降低。

3 动态刚度仿真分析

为了进一步探究弹簧振子隔离器模型的动态特性，笔者构建了该弹簧振子隔离器模型，对其进行了模态分析和谐响应分析，并与动刚度的试验结果进行对比；对其进行瞬态响应分析，与冲击刚度的试验结果进行对比。

模态分析和谐响应分析结果见图19 和图20。弹簧振子隔离器模型的模态仿真分析一阶固有频率为9.913 Hz，仿真结果与振动激励法的试验结果9.978 Hz 误差极小。在模态分析的基础之上，对其继续进行谐响应分在10 Hz 处发生共振，对应的放大倍数为12.5 倍，谐响应分析放大倍数结果与试验传递率放大倍数11.31 接近，误差较小。

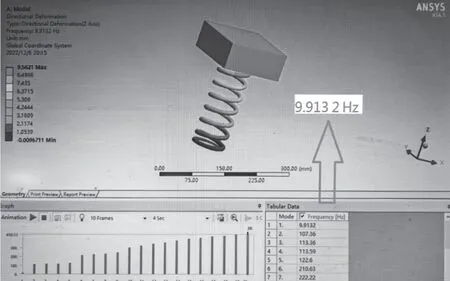
图19 模态分析示意图

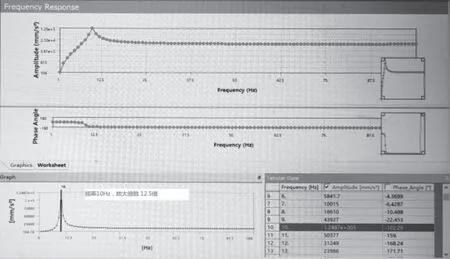
图20 谐响应分析示意图

瞬态响应仿真分析的速度输入曲线见图21。为确保瞬态响应分析的输入与冲击刚度试验的输入保持一致性，笔者采用了跌落速度为4.7 m/s 状态下的速度输入信号作为瞬态响应的输入分析，并将该输入信号加载于弹簧振子隔离器模型的底部。

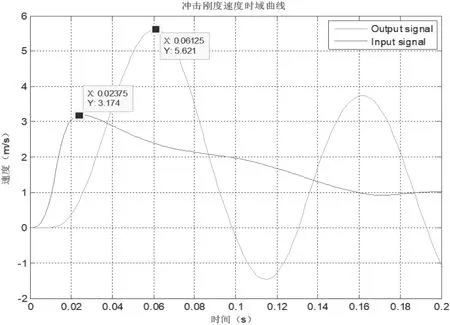
图21 瞬态响应仿真分析的速度输入曲线（提取黑色的输入速度作为输入）

瞬态响应仿真分析结果见图22。弹簧振子隔离器模型瞬态响应仿真分析的输出端速度曲线显示，在0.063 s 时刻，输出端最大速度为5.749 m/s。根据试验结果显示，弹簧振子隔离器模型冲击刚度的速度曲线显示，在0.061 25 s 时刻，输出端最大速度为5.621 m/s。仿真瞬态响应分析结果与跌落法冲击刚度试验结果接近。

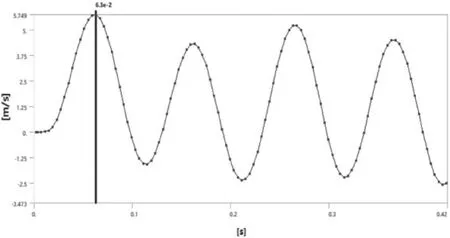
图22 输出端速度瞬态响应分析结果

4 结束语

本文对隔离器弹簧振子模型进行了试验测试和仿真分析，研究了动态刚度测试的关键点，但是对于隔离器的动态特性影响参数研究还不够深入全面。如带有大阻尼的非线性隔离器、带限位器的隔离器以及特殊材料隔离器的动态刚度测试方法研究有待后续深入研究。根据试验仿真研究情况，可以得出如下结论：

1）隔离器动态刚度测量有多种测量方法，需要根据加载载荷、隔离器种类和试验设备多方面考虑，择优选择试验方法，可以提高试验效率和准确度。

2）弹簧振子隔离器模型的动态刚度特性为动态变量，动刚度在整个频率带都不是恒定的，而冲击刚度受到加载速度影响。

3）动刚度和冲击刚度测试，需要根据隔离器的使用环境来确定考核边界，以便合理地对试验件做出有效考核。例如隔离器的额定承载下，动刚度以最大动刚度指标作为参考指标，冲击刚度以在一定冲击速度范围的平均冲击刚度或某个冲击速度之下的冲击刚度作为参考指标。