基于DGLPP-SVDD算法的化工过程故障检测
2024-04-26孙四通李师庆
孙四通 李师庆


作者简介:孙四通(1964-),副教授,从事过程优化与故障检测方向的研究,slsyjs2023@126.com。
引用本文:孙四通,李师庆.基于DGLPP-SVDD算法的化工过程故障检测[J].化工自动化及仪表,2024,51(2):310-318.
DOI:10.20030/j.cnki.1000-3932.202402021
摘 要 为解决传统全局局部保留投影算法(GLPP)不能充分利用已有故障数据进行特征提取的缺点,提出了判别全局局部保留投影算法(DGLPP)。在数据降维处理后,为应对高斯和非高斯混合分布的过程数据特性,通过支持向量数据描述算法(SVDD)构建故障检测统计量。将两种算法相结合提出基于DGLPP-SVDD的故障检测方法。将DGLPP-SVDD算法应用于TE过程仿真,并与GLPP算法对比,结果表明:DGLPP-SVDD算法具有更短的故障检测滞后时间和更高的故障检测率。
关键词 特征提取 DGLPP-SVDD算法 图嵌入 故障检测 全局局部保留投影 支持向量数据描述
中图分类号 TP277 文献标志码 A 文章编号 1000-3932(2024)02-0310-09
为了预防化工事故的发生以及在发生故障时能够及时报警,构建一个针对化工过程的故障检测模型至关重要。在化工生产过程中,采集到的数据一般都具有高维度的特点,为此普遍在构造故障检测模型前先进行数据特征提取或特征选择来压缩数据维度[1]。数据特征提取方法旨在保留高维数据的特性,目前主要有两种类型的算法分别从全局角度和局部角度进行特征提取。以主成分分析(PCA)[2,3]及其变体为代表的全局方法通过保持数据的最大方差来学习数据的全局信息,但此类方法忽略了数据的局部信息。以局部保留投影(LPP)[4~6]及其变体为代表的流形学习方法旨在提取数据的局部近邻信息,但此类方法忽略了由方差信息和高阶统计量表示的全局信息。针对这些方法存在的问题,LUO L J提出了全局局部保留投影算法(GLPP)来提取全局和局部特征[7]。在此基础上,文献[8]提出非线性动态全局局部保留投影(NDGLPP)算法;同时还有一些基于核函数和稀疏性的GLPP变体[9~11]。然而基于GLPP及其变体的故障检测方法并沒有充分利用已有的故障数据,而是仅依靠对正常工况数据进行特征提取来实现故障检测。对于一个真实的工业过程,即使不可能收集到所有类型的故障数据,但历史数据库中总是有一些已知的故障数据,而这些先验故障数据可以为在线故障检测提供一些非常有价值和强大的故障判别信息[12,13]。因此在GLPP基础上,有必要通过考虑利用已有故障数据进行扩展来提取有利于故障检测的判别特征。
数据降维后需要构建统计量以检测是否发生故障。常用的统计量有T2和SPE,但其受限于数据服从高斯分布的假设(实际工业生产中数据通常是高斯和非高斯混合分布)[14]。支持向量数据描述(SVDD)算法不受数据服从高斯分布的限制,并且能够处理非线性数据,目前已广泛应用于故障检测领域[15,16]。
综上所述,为充分利用先验故障数据来提取判别特征,笔者在图嵌入框架下对GLPP算法进行判别扩展,提出了DGLPP算法。数据降维后,使用SVDD在数据高斯和非高斯混合分布的情况下构建合适的统计量,从而提出基于判别全局局部保留投影和支持向量数据描述(DGLPP-SVDD)的故障检测算法,并通过TE过程仿真验证该方法的有效性。
1 算法描述
1.1 DGLPP算法
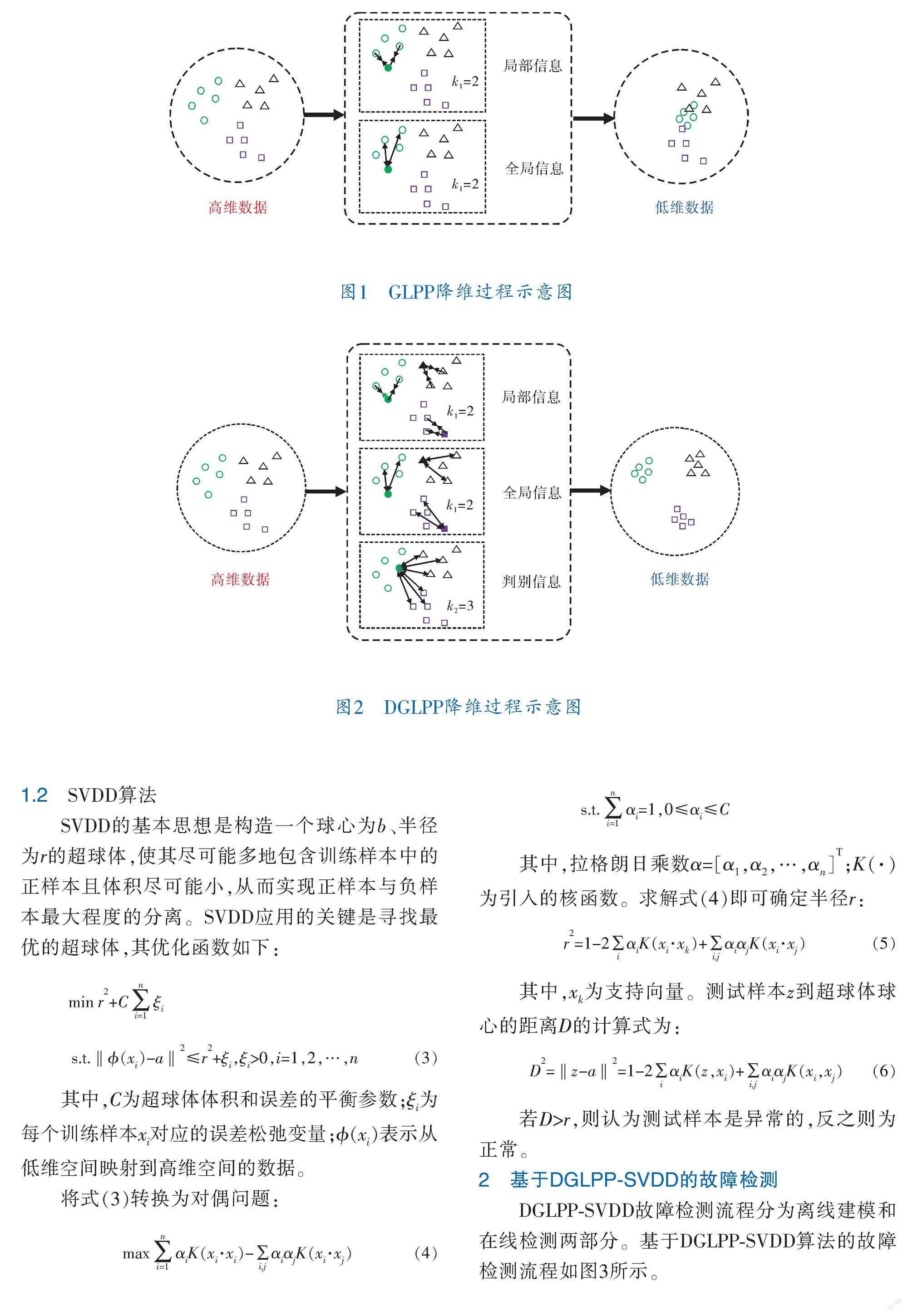
基于GLPP算法的描述[7],笔者在图嵌入框架下将其扩展为DGLPP算法。与GLPP训练样本只包含正常数据不同,DGLPP的训练样本包括正常数据和各类故障数据。对于m维n个样本点组成的数据矩阵X=[x,x,…,x]∈R,寻找一个合适的降维转换矩阵A∈R,通过Y=AX变换,得到维度为l(l J=min(y-y)W?摇J=-min(y-y)?摇J=-min(y-y)?摇 (1) 其中,J是指降维时保留类内样本的局部信息;J是指保留类内样本的全局信息;J是指保留正常样本和故障样本之间的判别信息;y、y表示低维空间中的样本点;W、W、分别表示高维空间中构造的3个权重矩阵,以表征3个有不同边连接关系的图结构。若高维空间的样本点xi和xj在图中存在边连接,则权重矩阵中对应的元素值以热核法表示,即exp(-‖x-x‖/t)(其中,t为经验参数,‖·‖表示欧氏距离);若x和x之间不存在边连接,则3个权重矩阵W、W、中对应的元素为零。 3个图结构中样本点之间存在连接边的条件不同:在类内局部图中条件为样本点x和x为类内k近邻关系;在类内全局图中条件为样本点x和x不是类内k近邻关系;在类间判别图中条件为正常样本点x和每类故障样本点x为类间k近邻关系。为了平衡3个子优化目标的关系,引入权重系数η来构成一个整体优化函数。DGLPP的优化函数表达式如下: J=min{η(J+J)+(1-η)J} =min(y-y)2R (2) =min(aXHXa-aXRXa)=min(aXMXa) s.t. aa=1 R=η(W-)-(1-η)W 其中,H为对角矩阵(H=R),拉普拉斯矩阵M=H-R;a为降维转换向量。最终的优化问题可以转换为求Ma=λa(λ为矩阵特征值)的广义特征值,从而得到降维转换矩阵A。η是一个介于0和1之间的值,用于平衡子目标函数间的重要性,其值对总体目标函数具有较大影响。η值的选取准则为:ηρ(W-)=(1-η)ρW,其中ρ(·)代表矩阵的谱半径。 图1、2分别为GLPP、DGLPP降维过程示意图。假设在高维空间中有3类数据,圆点代表正常运行数据。GLPP通过在正常数据中构造局部图和全局图进行降维。DGLPP通过构造类内局部图、类内全局图和类间判别图进行降维。以样本间的最近邻距离和类别为依据,设置样本点在图中的边连接关系,同类别样本设置k=2近邻,正常样本与各类故障样本间设置k=3近邻。图1、2中以标黑样本点为例显示与其他样本之间的边连接关系,边上的箭头方向表示降维时力作用的方向。图1中,在局部图中有边连接关系的正常样本点会相互吸引,而在全局图中会相互排斥,从而使得正常数据在低维空间中出现类内聚集且整体形状保持的效果,但GLPP对异常类数据并无约束,可能导致在低维空间中出现正常数据和异常数据相互交叠的情况,从而影响后续故障检测效果。图2中,在类内局部图中有边连接关系的样本点会类内相互吸引,在类内全局图中有边连接关系的样本点会类内相互排斥,在类间判别图中有边连接关系的正常样本和故障样本相互排斥,从而实现降维后类内样本聚集且整体形状保持并且正常数据与故障数据相互远离的效果。 1.2 SVDD算法 SVDD的基本思想是构造一个球心为b、半径为r的超球体,使其尽可能多地包含训练样本中的正样本且体积尽可能小,从而实现正样本与负样本最大程度的分离。SVDD应用的关键是寻找最优的超球体,其优化函数如下: min r+Cξ s.t.‖?准(x)-a‖≤r+ξ,ξ>0,i=1,2,…,n (3) 其中,C为超球体体积和误差的平衡参数;ξ为每个训练样本x对应的误差松弛变量;?准(x)表示从低维空间映射到高维空间的数据。 将式(3)转换为对偶问题: maxαK(x·x)-ααK(x·x) (4) s.t.α=1,0≤α≤C 其中,拉格朗日乘数α=[α,α,…,α];K(·)为引入的核函数。求解式(4)即可确定半径r: r=1-2αK(x·x)+ααK(x·x) (5) 其中,x为支持向量。测试样本z到超球体球心的距离D的计算式为: D=‖z-a‖=1-2αK(z,x)+ααK(x,x) (6) 若D>r,则认为測试样本是异常的,反之则为正常。 2 基于DGLPP-SVDD的故障检测 DGLPP-SVDD故障检测流程分为离线建模和在线检测两部分。基于DGLPP-SVDD算法的故障检测流程如图3所示。 离线建模流程如下: a. 载入正常工况和故障工况数据组成训练集,求取正常数据的平均值和标准差,然后对整个数据集进行标准化处理。 b. 设置相关参数,构造3个图结构,采用DGLPP算法求取降维转换矩阵A。求取整个数据集的低维投影数据Y=AX和正常数据的低维投影数据Y=AX。 c. 用Y作为SVDD算法的训练集,训练SVDD算法模型,得到超球面中心和半径。 在线检测流程如下: a. 载入测试数据x,并用离线建模时的平均值和标准差进行标准化; b. 获得测试数据x在低维空间中的表示Y=AX; c. 将Y作为已训练好的SVDD算法测试集,计算样本点到超球面中心的统计量D,并判断是否超过控制限。 3 仿真与结果分析 3.1 实验数据集 TE过程是美国伊斯曼公司根据真实化工过程开发的一个仿真平台,其产生的数据具有时变、强耦合和非线性特征,广泛用于测试复杂工业过程的控制和故障诊断模型[17~19]。TE过程主要由反应器、冷凝器、气液分离塔、压缩机和汽提塔5部分组成,其工艺流程如图4所示。TE生产过程主要由4种气态物料参与反应,分别为A、C、D和E,生产出两种产品G、H,并伴有一种副产品F,此外在产品的进料中会含有少量的惰性气体B。生产过程为:首先将物料A、C、D、E送入反应器,然后将产物送入冷凝器,冷凝后的产物进入汽液分离器,气相组分经压缩机循环后进入反应器,液相组分进入汽提塔与剩余的反应物分离,然后分离得到产物G和H。 TE过程包括22个过程测量变量、19个成分测量变量和12个操作变量,具体变量描述可见文献[18]。TE仿真控制系统中共预设有21种不同的故障,全部故障描述可见文献[19]。笔者选取与文献[19]相同的34个变量用于构建监控模型,即22个过程测量变量和12个操作变量。使用广泛采用的数据集进行训练和测试,此数据集中包括正常工况的仿真数据和21类故障数据。每类数据包括480个样本点的训练集和960个样本点的测试集,故障测试集中从第161个样本处引入故障,样本点的采样间隔为3 min。 3.2 仿真设置及结果分析 在GLPP降维算法的基础上加以改进得到DGLPP降维算法,并与文献[19]中的GLPP-T2和GLPP-SPE算法作对比,即通过在GLPP降维后的主元空间建立T2统计量和在残差空间中建立SPE统计量,研究笔者算法在TE过程上的故障检测性能。根据文献[19]对GLPP故障检测算法做相同的设置,k1近邻数目设为10,降维后保留16个维度;热核参数t设为距离平均值;设定T2和SPE控制限的置信度为99%。为定量对比,对DGLPP做相似的参数设置,类内k近邻数目设为10,类间k近邻数目设为20,降维后保留16个维度;t设为距离平均值;设定SVDD算法中高斯核参数为8,参数C=0.05。为了对比DGLPP与GLPP的故障检测性能,笔者采用故障检测滞后时间、故障检测率(FDR)和故障误报率(FAR)来表征对TE过程中21个故障的检测性能。其中,故障检测滞后时间是指故障发生后到第1次检测出故障的时间,FDR是指检测出来的故障样本数占总故障样本数的比值,FAR是指正常数据中误报的样本个数占正常数据的比值。TE过程21个故障的故障检测滞后时间、FAR和FDR见表1。已有研究证明,故障3、9、15难以通过数据驱动方法进行检测,故在表1中记录了去除这3个故障后的平均值(平均值*)。 从表1可以看出,对于易于检测的故障(如故障1、2、6、7、8、13、14),3种方法的故障检测率都比较高。对于GLPP-T2和GLPP-SPE难以检测的故障(如故障4、11、19),采用DGLPP-SVDD可以有更高的故障检测率。对于所有方法来说,检测故障3、9、15都是极其困难的,这是因为它们对测量变量的平均值、方差或峰值时间影响很小。总体来看,DGLPP-SVDD算法的平均故障误报率相比于GLPP-T2和GLPP-SPE算法有一定上升,但从提高故障检测率效果来看,代价是可以接受的。DGLPP-SVDD算法有更高的故障检测率和更短的故障检测滞后时间,这是因为在提取正常数据和故障数据间的判别信息后对故障更加敏感。 笔者选择故障5(阶跃故障)、故障10(随机故障)和故障19(未知故障)进行具体分析对比,检测结果如图5~7所示。故障5的原因是由于冷凝器冷却水进口温度发生阶跃变化。该变化导致系统增加冷凝器冷却水流速以补偿温度变化。此外,当故障发生时从冷凝器到分离器的物料流速也发生变化,这进一步增加了分离器中的温度。然而控制回路可以补偿这种变化,使得分离器温度可以在大约第360个采样之后返回到初始设定点。从图5可以看出,GLPP-T2算法可以在第161个样本点检测到故障,并且可以一直持续报警。GLPP-SPE算法可以在第161个样本点检测到故障,但受到TE工艺的闭环反馈特性影响,在第360个采样点之后无法对故障实现有效检测。DGLPP-SVDD算法可以在第161个采样点检测到故障,并且可以持续检测故障。 图5 故障5检测结果 图6 故障10检测结果 图7 故障19检测结果 故障10的原因是物料C的温度发生随机变化,由于物料C被送入汽提塔,故该故障导致汽提塔温度持续波动。汽提塔蒸汽阀通过改变整个过程中的开度来缓解汽提塔温度变化,这意味着该故障影响系统操作条件动态变化,故检测结果也是上下波动变化。从图6可以看出,GLPP-T2算法可以在第175个采样点处检测到故障,DGLPP-SVDD算法可以在第166个样本点检测到故障,从故障检测延迟角度看,DGLPP-SVDD算法效果更优。从故障检测率角度看,DGLPP-SVDD算法和GLPP-T2算法都可以检测出该故障,而GLPP-SPE算法的故障检测率却很低。 故障19为未知故障,无法从工艺机理上进行分析。从图7可以看出,GLPP-T2和GLPP-SPE算法在故障19发生后基本检测不到;DGLPP-SVDD算法可以在第161个采样点处检测到故障19,并可以对其持续检测报警到结束,故障检测率较高。 4 结束语 笔者提出了基于判别全局局部保留投影-支持向量数据描述的故障检测算法。DGLPP降维算法是在GLPP的基础上扩展而来,解决了传统GLPP不能利用先验故障数据的问题。DGLPP通过构建3个图结构同时保留数据的局部信息、全局信息和基于故障样本的判别信息,提取到有利于后续故障检测的低维特征,在数据降维后利用SVDD算法处理非高斯数据的优势构建监控统计量,提高了算法的故障检测性能。在TE过程仿真平台上与GLPP算法进行对比,结果证明了DGLPP-SVDD有更高的故障检测率和更短的检测滞后时间。提出的图嵌入框架下的改进策略,可為其他故障检测方法提供改进思路。 参 考 文 献 [1] 姚羽曼,罗文嘉,戴一阳.数据驱动方法在化工过程故障诊断中的研究进展[J].化工进展,2021,40(4):1755-1764. [2] RUSSELL E L,CHIANG L,BRAATZ R D.Fault detection in industrial processes using canonical variate analysis and dynamic principal component analysis[J].Chemometrics and Intelligent Laboratory Systems,2000,51(1):81-93. [3] DENG X G,TIAN X M,CHEN S,et al.Fault discriminant enhanced kernel principal component analysis incorporating prior fault information for monitoring nonlinear processes[J].Chemometrics and Intelligent Laboratory Systems,2017,162:21-34. [4] HE X F,NIYOGI P.Locality preserving projections[J].Advances in Neural Information Processing Systems,2003,16(1):186-197. [5] 张学磊,徐进学,祝朋艳.基于改进核局部保持投影的故障检测方法研究[J].计算机应用与软件,2022,39(5):115-124;131. [6] ZHONG F J,ZHANG J S,LI D F.Discriminant Locality Preserving Projections Based on L1-Norm Maximization[J].IEEE Transactions on Neural Networks and Learning Systems,2014,25(11):2065-2074. [7] LUO L J.Process monitoring with global-local preserving projections[J].Industrial & Engineering Chemistry Research,2014,53(18):7696-7705. [8] 徐靜,王振雷,王昕.基于非线性动态全局局部保留投影算法的化工过程故障检测[J].化工学报,2020,71(12):5655-5663. [9] 徐静,王振雷,王昕.基于DGLPP-SVDD算法的化工过程故障检测[J].控制工程,2021,28(12):2462-2468. [10] LUO L J,BAO S Y,MAO J F,et al.Nonlinear process monitoring based on kernel global-local preserving projections[J].Journal of Process Control,2016,38:11-21. [11] BAO S Y,LUO L J,MAO J F,et al.Improved fault detection and diagnosis using sparse global-local preserving projections[J].Journal of Process Control,2016,47:121-135. [12] 郭小萍,尹瑞琛,李元.基于MDP-SVM的过程多类型故障诊断[J].电子测量技术,2022,45(1):159-164. [13] 常书源,赵荣珍,陈博,等.基于边界判别多流形分析的故障数据集降维方法[J].振动与冲击,2021,40(23):120-126. [14] LUO L J,XU M,BAO S Y,et al.Improvements to the T2 statistic for multivariate fault detection[J].Industrial & Engineering Chemistry Research,2019,58(45):20692-20709. [15] TAX D M J,DUIN R P W.Support vector data description[J].Machine Learning,2004,54:45-66. [16] HUANG J,ERSOY O K,YAN X F.Fault detection in dynamic plant-wide process by multi-block slow feature analysis and support vector data description[J].ISA Transactions,2019,85:119-128. [17] 顾炳斌,熊伟丽.基于多块信息提取的PCA故障诊断方法[J].化工学报,2019,70(2):736-749. [18] GE Z Q,SONG Z H.Distributed PCA model for plant-wide process monitoring[J].Industrial & Engineering Chemistry Research,2013,52(5):1947-1957. [19] HUANG C H,CHAI Y,LIU B W,et al.Industrial process fault detection based on KGLPP model with Cam weighted distance[J].Journal of Process Control,2021,106:110-121. (收稿日期:2023-03-28,修回日期:2024-01-23) Failure Detection in Chemical Process Based on DGLPP-SVDD Algorithm SUN Si-tong, LI Shi-qing (College of Automation and Electronic Engineering, Qingdao University of Science and Technology ) Abstract Considering the fact that traditional global locality preserving projection(GLPP) algorithm fails to make full use of the existing failure data for feature extraction, a discriminant global locality preserving projection (DGLPP) algorithm was proposed. For purpose of dealing with the process data characteristics of Gaussian and non-Gaussian mixture distribution, The data dimension reduction was completed and the support vector data description(SVDD) algorithm was used to construct fault detection statistics, including having two algorithms combined to propose a fault detection method based on DGLPP-SVDD. Applying the DGLPP-SVDD algorithm to TE process simulation and compared with GLPP algorithm shows that, the DGLPP-SVDD algorithm has shorter fault detection lag time and higher fault detection rate. Key words feature extraction, DGLPP-SVDD algorithm, graph embedding, failure detection, GLPP, SVDD
