基于自适应无迹卡尔曼滤波算法的锂电池荷电状态预测
2024-04-26蒙永龙艾学忠郑巍王明达汪冬冬
蒙永龙 艾学忠 郑巍 王明达 汪冬冬


基金项目:吉林省科技发展计划(批准号:20190302063GX)资助的课题。
作者简介:蒙永龙(1996-),硕士研究生,从事检测技术与自动化装置的研究。
通讯作者:艾学忠(1970-),教授,从事检测技术与自动化装置的研究,1135916263@qq.com。
引用本文:蒙永龙,艾学忠,郑巍,等.基于自适应无迹卡尔曼滤波算法的锂电池荷电状态预测[J].化工自动化及仪表,2024,51(2):294-300.
DOI:10.20030/j.cnki.1000-3932.202402019
摘 要 针对无迹卡尔曼滤波在噪声不稳定和工况复杂的情况下锂电池荷电状态预测准确度低的问题,提出基于二阶等效RC电路模型,采用遗忘因子递推最小二乘法对模型参数进行辨识,使用自适应无迹卡尔曼滤波算法(AUKF)对锂电池荷电状态进行预测,最后在DST数据工况下,验证预测模型的准确性。对无迹卡尔曼滤波(UKF)算法和提出的AUKF算法进行仿真对比,结果表明:所提算法的最大误差在±0.02之内,预测精度更高、适用性更强。
关键词 锂电池 荷电状态 自适应无迹卡尔曼滤波 遗忘因子递推最小二乘
中图分类号 TM912 文献标志码 A 文章编号 1000-3932(2024)02-0294-07
锂电池的荷电状态(State of Charge,SOC)是电动汽车电池管理系统的重要数据之一,它可以提供有关车辆电池管理策略的信息。目前,锂电池的荷电状态只能间接测量,通过路端电压、放电电流及内阻等参数去预测是现在常用的方法。锂电池荷电状态预测的精准度直接影响着电池的寿命和安全性能[1]。
锂电池荷电状态的预测方法主要有以下两种:
a. 依照锂电池各项数据计算得出,如电流积分法和开路电压法[2];
b. 对电池建模然后引入算法预测,如粒子滤波算法、BP算法及卡尔曼滤波(KF)算法等。
当初始容量已知时,电流积分方法计算电流随时间的积分,以获得流入或流出电池的电量,从而获得剩余电量[3]。该方法操作简单、稳定,在短时间内具有较高的精度。然而,当长时间测量电流时,可能会出现累积误差,导致估计精度下降。开路电压法需要知道电池的开路电压和荷电状态之间的特性关系,由于电池电动势和开路电压之间的误差很小,可以通过测量电池静置电动势来找到相应的荷电状态,但实验过程需要很长时间,不利于研究[4]。神经网络方法在样本学习过程中不断更新模型的权重和误差,以提高模型的准确性。该算法可以在一定条件下准确快速地估计电池的荷电状态,但仍面临许多问题,如样本算法的计算和存储需要大量训练,难以建立准确的模型[5];粒子滤波算法运算繁杂[6];KF算法比较依赖模型的精度。在模型精確的基础上,KF滤波算法的荷电状态预测精度较好[7]。
传统的KF算法用于非线性系统时精度低、效果差,所以很多学者提出扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法与无迹卡尔曼滤波(Unscented Kalman Filter,UKF)算法[8]。EKF用在非线性系统效果差且雅可比矩阵运算繁杂;UKF通过U变化得到Sigma点集,经过非线性处理后得到结果,然后用此结果更新均值和协方差[8]。UKF在预测锂电池的荷电状态时,系统噪声繁杂,预测精度低。
笔者针对UKF估计荷电状态时预测精度与实用性不理想等问题,提出自适应的无迹卡尔曼滤波算法(AUKF),在系统预测时一直更新状态噪声协方差与测量噪声协方差,从而提升算法的精度和鲁棒性。
1 锂电池模型的建立及参数辨识
1.1 建立等效锂电池模型
因为电池内部是非线性的,所以建立优良的锂电池模型是荷电状态估算的基础。传统的一阶RC模型预测精度较低,理论上来说模型的阶数越多越贴近真实状态,但是模型参数计算会越复杂,综合考虑之后,决定采用二阶RC模型来对锂电池建模,电路如图1所示[9]。
图1 等效电路模型
该二阶RC锂电池模型由欧姆内阻R、极化电容C、极化电阻R、极化电容C、极化电阻R、开路电压U和端电压U组成。由基尔霍夫定律知[10]:
U=U(SOC)-U-U-I(t)R (1)
=-+ (2)
=-+ (3)
其中,I为锂电池内部发的环路电流;U、U分别为R、C两端的电压与R、C两端的电压。
由式(1)~(3)建立电池连续系统方程:
U=U(SOC)-I(t)R-I(t)R(1-e)-
I(t)R(1-e) (4)
其中,Δt为采样周期;τ=RC,τ=RC,表示图1中两个RC电路的时间响应常量。
1.2 等效锂电池模型参数辨识
使用INR18650-20R电池,容量2 000 mAH,标称电压为3.7 V,充电电压为4.2 V,放电截止电压为2.75 V。在动态应力测试(Dynamic Stress Test,DST)工况下测试电压电流数据。然后采用遗忘因子递推最小二乘算法辨识模型参数,该算法首先要将等效电路转化为最小二乘的形式。将式(1)进行拉氏变换[11]:
U(s)-U(s)=I(s)R++ (5)
其中,s为Laplace算子,线性变换公式为:
s= (6)
其中,z为离散z域上的对应算子;T为采样周期。通过线性处理实现连续系统与离散系统的转变,系统z域上的传递函数由s域映射到z域得到,化简后的公式为:
G(z)== (7)
其中,θ、θ、θ、θ、θ分别是k时刻的简化代表系数,表达式为:
θ=θ=-1θ= θ=θ=(8)
其中,a=R;b=ττ;c=τ+τ;d=R+R+R;e=R(τ+τ)+Rτ+Rτ;τ=RC;τ=RC。
将式(7)离散化得:
y(k)=θy(k-1)+θy(k-2)+θI(k)+
θI(k-1)+θI(k-2)(9)
最小二乘法的观测向量为:
φ(k)=((y(k-1),y(k-2),I(k),I(k-1),I(k-2))
待估计参数向量为:
θ(k)=θ,θ,θ,θ,θ
由式(8)可得:
a=b=c=d=e= (10)
结合以上公式可得:
R=aR=[τ(d-a)+ac-e]/(τ-τ)R=R-d+aC=τ/RC=τ/R (11)
τ=
τ=(12)
系统的待估计参数向量是θ(k),增益系数是K(k),协方差矩阵是P(k),遗忘因子最小二乘递推方程为:
K(k)=P(k)=[I(k)-K(k)φ(k)]P(k-1)θ(k)=θ(k-1)+K(k)[U(k)-U(k)-θ(k-1)φ(k)](13)
其中,λ为遗忘因子,取值范围为0.95≤λ≤1,本研究中取0.997。用增益系数K(k)不断地修正更新系统观测向量φ(k)和实际观测值y(k)的差值。
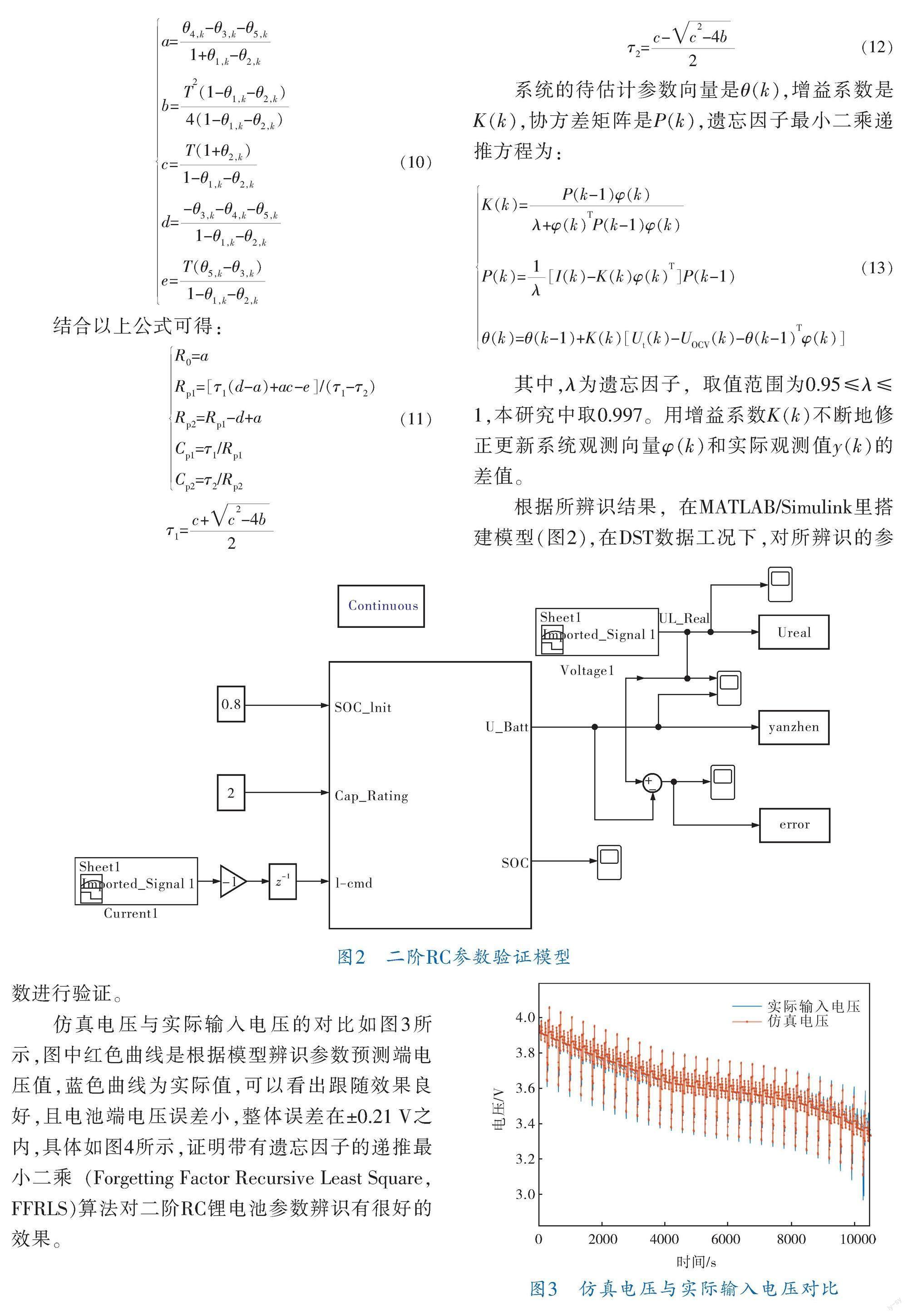
根据所辨识结果,在MATLAB/Simulink里搭建模型(图2),在DST数据工况下,对所辨识的参数进行验证。
仿真电压与实际输入电压的对比如图3所示,图中红色曲线是根据模型辨识参数预测端电压值,蓝色曲线为实际值,可以看出跟随效果良好,且电池端电压误差小,整体误差在±0.21 V之内,具体如图4所示,证明带有遗忘因子的递推最小二乘(Forgetting Factor Recursive Least Square,FFRLS)算法对二阶RC锂电池参数辨识有很好的效果。
图3 仿真电压与实际输入电压对比
图4 模型误差
2 基于AUKF算法的锂电池荷电状态预测
根据图1所示二阶RC电路,分别用两个RC电路两端的电压U和U锂电池荷电状态结合为状态变量X=[U,U,SOC],所以锂电池荷电状态的状态方程为:
X=AX+BU(k)+w(k) (14)
測量方程为:
Z(k)=U[SOC(k)]-U(k)-U(k)-I(k)R+v(k)(15)
X=U(k+1)U(k+1)SOC(k+1)
A=1- 0 0 0 1- 0 0 0 1
B=-
其中,v(k)代表系统的测量噪声;w(k)代表系统的过程噪声;Q代表锂电池的电池容量[12]。
UKF算法的主要思想是U变换,用U变换处理均值与协方差的非线性传递,用一系列确定样本来贴近状态的概率分布,并不是对非线性函数近似,避免了计算繁杂的雅可比矩阵。AUKF预测锂电池荷电状态的过程如下。
a. Sigma点和相应权值的构造。
给出输入变量x的Sigma点采样方法,求出Sigma点集{x}(i=0,1,2,…,2n,n是状态变量维度),利用输出的统计信息得到期望权重w和方差权重w,再对{x}非线性变换求出{y},最后求出y的平均值和协方差P[13]。
b. 给协方差P0和误差0设置初值。
=E(x)P=E[(x-)(x-)] (16)
c. 计算Sigma点、状态变量预测以及协方差更新。
x= ,i=0+() ,1≤i≤n-(),(n+1)≤i≤2n(17)
x=f(x,u) (18)
=wx (19)
P=w=(x-)(x-)+Q(20)
其中,λ为调节变量,λ=α(n+β)-n(α、β是比例因子);x为k-1时刻的第i个采样点,用来控制平均值到点的间距;u为k-1时刻的输入;Q为系统噪声协方差矩阵。
d. 更新观测变量。
y=h(x,u) (21)
=wy (22)
e. 更新误差协方差以及卡尔曼增益。
P=w(y-)(y-)+R (23)
P=w(y-)(y-) (24)
Kk= (25)
=+K(y-) (26)
P=P-KPK(27)
其中,K为卡尔曼增益矩阵;k|k-1为基于k-1时刻对k时刻的估计值;k|k表示在k时刻时,已经经过了预测和更新步骤,综合考虑了系统动态和观测数据,得到的最终状态估计值,用于表示系统在时刻k时的最优估计状态;R为观测噪声协方差矩阵。
分别把状态方程与测量方程(14)、(15)代进上述AUKF算法,经过不断地更新计算,使荷电状态不断贴近真实值。当UKF用于评估状态变量时,测量误差和噪声系统通常为固定值。然而,锂电池系统是一个非线性系统,随着算法重复次数的增加,会导致误差累积,甚至产生不同的结果。因此,为了提高荷电状态准确性,有效减少噪声对过滤结果的影响,需要加入自适应协方差匹配方法。
系统在k时刻的误差为e,自适应算法为:
H=ee (28)
R=H-CCQ=KHK (29)
其中,H为估算协方差函数;M为累计新息数量,在这里取3.2。将Q、R代入式(20)、(23)中进行自适应更新。
3 仿真验真與分析
锂电池在实际使用的时候,工况复杂,因此使用DST工况对算法进行验证。笔者使用INR 18650-20R电池,容量为2 000 mAH,标称电压为3.7 V,充电电压为4.2 V。由于过度放电会使锂电池寿命缩短,因此在DST工况循环15次后停止放电。在MATLAB中编写AUKF算法并进行锂电池荷电状态的预测,结合所得数据进行仿真验证。图5为算法仿真模型。
以电流积分法计算出的荷电状态为参考值,模型输入电流、电压如图6、7所示。图8为荷电状态预测结果,AUKF能实时更新系统噪声且通过噪声协方差更新荷电状态预测值,从仿真图中可以看出AUKF算法对荷电状态的预测效果比UKF要好,能够快速贴近参考值且波动情况小于UKF。图9为两种算法的误差对比,可以看到,无迹卡尔曼滤波算法预测偏差较大,最大误差为0.03,相比而言,加入自适应因子的无迹卡尔曼滤波算法预测效果较好,预测误差保持在了±0.02以内,验证了AUKF算法对滤波发散的控制作用。
图6 DST工况电流数据
图7 DST工况电压数据
图8 UKF和AUKF算法估计荷电状态的曲线
图9 UKF和AUKF算法估计荷电状态误差曲线
4 结束语
基于二阶RC等效电路模型完成锂电池建模,然后通过带有遗忘因子非线性最小二乘算法实现模型参数辨识,通过仿真模型验证了锂电池模型参数的优良性能。在未知噪声的影响下,传统UKF算法的预测准确度不高。因此,引入带有自适应因子的UKF算法来预测锂电池的荷电状态。仿真结果表明,通过自适应调整后的UKF算法,将最大误差控制在了±0.02之内,具有良好的稳定性和准确性。
参 考 文 献
[1] 刘鹏,李云伍,梁新成.基于遗忘递推最小二乘与自适应无迹卡尔曼滤波的锂电池SOC估计[J].汽车技术,2022,7(2):21-27.
[2] YANG F,SHI D,MAO Q,et al.Scientometric research and critical analysis of battery state-of-charge estimation[J].Journal of Energy Storage,2023,58:106283.
[3] 陆张浩,潘正军,许祥进.车用锂离子电池的SOC估算方法研究现状[J].时代汽车,2021(6):161-162.
[4] SHE C,WANG Z,SUN F,et al.Battery aging assessment for real-world electric buses based on incremental capacity analysis and radial basis function neural network[J].IEEE Transactions on Industrial Informatics,2019,16(5):3345-3354.
[5] 董策勇,李红月.基于改进UKF算法的锂电池SOC估计[J].绿色科技,2022,24(14):247-250.
[6] 王向标,张庭芳,曹铭,等.具有温度自适应性的二阶RC参数辨识模型[J].电源技术,2022,46(6):661-664.
[7] 汤惠淞,吴长水,吴习文.基于UKF算法的电池荷电状态SOC估算研究[J].软件导刊,2020,19(11):90-95.
[8] BARCELLONA S,CICCARELLI F,IANNUZZI D,et al.Modeling and parameter identification of lithium-ion capacitor modules[J].IEEE Transactions on Sustainable Energy,2014,5(3):785-794.
[9] 王浩,郑燕萍,虞杨.基于动态优选遗忘因子最小二乘在线辨识的磷酸铁锂电池SOC估算[J].汽车技术,2021(10):23-29.
[10] 张武,孙士山,张家福.基于自适应无迹卡尔曼滤波的动力电池SOC估计[J].电源技术,2021,45(1):14-17.
[11] EL D M S,HUSSEIN A A,ABDEL-HAFEZ M F.Imp- roved battery SOC estimation accuracy using a modified UKF with an adaptive cell model under real EV operating conditions[J].IEEE Transactions on Transportation Electrification,2018,4(2):408-417.
[12] 田茂飞,安治国,陈星,等.基于在线参数辨识和AEKF 的锂电池SOC估计[J].储能科学与技术,2019,8(4):745-750.
[13] 曹銘,张越,黄菊花.基于RLS法的锂离子电池离线参数辨识[J].电池,2020,50(3):228-231.
(收稿日期:2023-04-05,修回日期:2024-01-22)
Prediction of Li-ion Battery Charge State Based on Adaptive Untraced Kalman Filtering Algorithm
MENG Yong-long, AI Xue-zhong, ZHENG Wei, WANG Ming-da, WANG Dong-dong
(College of Information and Control Engineering , Jilin Institute of Chemical Technology)
Abstract Considering the fact that unscented Kalman filter(UKF) has low accuracy in predicting Li-ion battery charge state in the case of unstable noise and complex working conditions, a model based on second-order equivalent RC circuit was proposed, including having the forgetting factor recursive least square(FFRLS) method employed to identify model parameters, and the UKF algorithm adopted to predict Li-ion charge battery state, as well as verify the accuracy of the prediction model in DST data condition. The simulation results show that, the maximum error of the proposed UKF algorithm stays within ±0.02, and its accuracy is higher and the applicability is stronger.
Key words Li-ion battery,charge state, UKF, FFRLS
