具有稚虫迁徙机制的S型自适应混沌蜉蝣算法

张恒齐 钱谦

基金项目：云南省科技厅基础研究专项（批准号：202101AT070082）资助的课题。

作者简介：张恒齐（1994-），硕士研究生，从事计算智能、智能信息处理等的研究。

通讯作者：钱谦（1981-），副教授，从事计算智能与视觉认知的研究，Qianqian_yn@126.com。

引用本文：张恒齐，钱谦.具有稚虫迁徙机制的S型自适应混沌蜉蝣算法［J］.化工自动化及仪表，2024，51（2）：262-273.

DOI：10.20030/j.cnki.1000-3932.202402016

摘 要 针对蜉蝣优化算法（MA）全局搜索能力较弱，对子代优秀个体有效信息利用不够充分的缺点，以及在计算中后期易陷入局部收敛，进而影响优化效果的问题，提出一种具有稚虫迁徙机制的S型自适应混沌蜉蝣优化算法（S-AMA）。S-AMA算法首先采用Logistic混沌映射产生蜉蝣种群，增加算法初期种群的多样性；随后，将蜉蝣生命周期进行数学建模，并引入S型生命系数替换原有的重力惯性系数，动态调整算法探索能力和开发能力間的平衡性；最后，根据蜉蝣在缺氧环境下的种群活动，引入稚虫迁徙机制强化子代优秀个体摆脱局部最优的能力，进而更加充分地搜索最优解附近的区域，以增强算法的收敛精度。实验部分将S-AMA应用于标准函数测试集，并分别进行优化对比实验、Wilcoxon秩和检验。结果表明：与对比算法相比，S-AMA算法具有更好的寻优能力、收敛速度及鲁棒性。

关键词 S型自适应混沌蜉蝣优化算法（S-AMA） 稚虫迁徙机制 混沌映射 S型生命系数 莱维飞行

中图分类号 TP18  文献标志码 A   文章编号 1000-3932（2024）02-0262-12

随着科学技术的不断创新发展，工程问题［1］实例的规模越来越大，相关问题计算的时间和空间复杂度呈指数上升。传统优化算法（如梯度下降［2］、牛顿法［3］）依赖于目标函数连续或可导，无法满足现实中具有复杂数学特性优化问题的求解需求。元启发式算法（Metaheuristic Algorithms，MAs）因不依赖于目标问题的梯度信息，易于布署，已被应用于动态网络社区发现［4］、路径规划［5］、线性天线阵列的模式合成优化［6］及集成风速预测系统［7］等领域。MAs大多是对自然界的生物行为学习研究后获得灵感启发而得，常见算法有粒子群算法（Particle Swarm Optimization，PSO）［8］、蜉蝣优化算法（Mayfly Algorithm，MA）［9］、哈里斯鹰优化算法（Harris Hawk Optimization，HHO）［10］、黏菌优化算法（Slime Mould Algorithm，SMA）［11］、灰狼优化算法（Grey Wolf Optimization，GWO）［12］等。但MAs存在一些缺陷，如收敛精度低、易陷入局部最优等，影响了算法的优化性能。NFL（No Free Lunch）理论同样指出不存在某种单一优化算法能够同时处理所有的工程问题［13］。因此，需要对传统元启发式算法进行改进，以优化其性能。

蜉蝣算法（Mayfly Algorithm，MA）是希腊学者Konstantinos Zervoudakis等受蜉蝣生物活动启发而提出的一种新型元启发式优化算法，用于解决复杂函数优化问题。迄今为止，MA已被应用于动态网络社区发现［4］、线性天线阵列的模式合成优化［6］、集成风速预测形态［7］等。说明MA相比于其他传统算法的求解精度高、收敛快，在工程领域受到学者们的青睐。但MA与其他群智能算法一样，搜索精度和收敛速度有待优化。因此，学者们对MA进行了改进，文献［14］提出一种基于Logistic映射的蜉蝣优化算法（LMA），通过Logistic映射对优秀蜉蝣进行扰动来防止种群出现早熟收敛现象；文献［15］提出了一种基于倒位变异的蜉蝣优化算法（IVMA），将倒位变异与突变结合，提高了算法在求解高维复杂问题时的收敛精度；文献［16］提出一种基于黄金正弦自适应融合的蜉蝣优化算法，通过引入黄金正弦因子和莱维飞行策略平衡了算法的全局搜索行为与局部搜索行为；文献［17］提出一种偏移进化蜉蝣优化算法，引入拉伸因子，通过偏移进化机制增强了算法的收敛性能；文献［18］提出一种增强全局搜索和自适应的蜉蝣算法，算法主要引入不完全伽玛函数与Beta累加分布的自适应的惯性权重平衡了算法的全局搜索与开发能力。上述文献所提方法在一定程度上提升了算法的性能，但是大多只是简单的策略或算法上的叠加。

如果将蜉蝣的优秀程度定义为根据问题模型求得的适应度值，则每个蜉蝣在搜索空间内的位置代表目标问题的一个潜在解决方案。虽然MA具有较好的局部搜索能力并能保持一定的种群多样性，但MA前期全局搜索能力较弱，导致算法后期的收敛精度较低，易陷入局部极值［9］。此外，MA迭代前期惯性系数较小，影响了蜉蝣种群的进化效率，具体地说，随着婚礼舞蹈系数和飞行系数的数值随迭代次数降低，算法后期的搜索步长越来越小，使种群难以跳出局部最优。为克服上述缺陷，增强种群的搜索效率，笔者提出一种具有稚虫迁徙机制的S型自适应混沌蜉蝣优化算法（S-type Adaptive Mayfly Algorithm Based on Larval Migration Mechanism，S-AMA）：

a. 种群初始化时加入Logistic混沌映射，以使种群位置分布更加均匀，同时保留一定随机性，以增加种群多样性，进而保证算法初始状态的搜索范围；

b. 模拟蜉蝣的生命周期，提出一种S型生命系数非线性参数控制策略平衡算法的探索与开发能力，以使算法能够拥有更快的收敛速度以及更好的收敛精度；

c. 针对蜉蝣稚虫能够在缺氧环境中寻找氧气充沛栖息地的能力，在蜉蝣交配行为产生优秀子代后加入稚虫迁徙机制，令子代蜉蝣能够更好地跳出局部最优，使其在后续搜索时更好地趋向于目标问题的最优解。

最后，选用蜉蝣优化算法（MA）［9］、粒子群算法（PSO）［8］、基于倒位变异的蜉蝣优化算法（IVMA）［15］、基于Logistic映射的蜉蝣优化算法（LMA）［14］、哈里斯鹰优化算法（HHO）［10］、灰狼优化算法（GWO）［12］等与S-AMA算法作对比，通过23个基准测试函数进行综合性能比较，来验证算法的有效性和优越性。

1 MA算法

MA算法的工作原理是：首先随机生成雄性蜉蝣和雌性蜉蝣两组种群作为算法的搜索代理群体，每个蜉蝣作为候选解被随机置放在问题空间中，用d维向量x=（x，x，…，x）表示，其优劣程度由问题模型的适应度函数f（x）评估。而蜉蝣位置变化的度量用速度v=（v，v，…，v）表示，每只蜉蝣的飞行方向由个体经验和社会经验共同决定，并且每只蜉蝣都会调整自己的运动轨迹，使其能够达到目前个人最佳位置pbest以及当前所有蜉蝣所达到的最佳位置gbest。

1.1 雄性蜉蝣运动

求偶天性促使所有雄性蜉蝣聚集在一起，意味着每只雄性蜉蝣的位置都会根据自己和周围邻居的经验进行调整。设x表示蜉蝣i在第t代的迭代中第j维的位置，那么其下一代位置x由当前位置与速度共同决定：

x=x+v，x∈（x，x）     （1）

其中，x為初始化后位于第j维的雄性蜉蝣i；x与x分别为雄性蜉蝣位置变化区域的最大值与最小值。

雄性蜉蝣的聚集行为会使它们总是在离水面几米的地方表演婚礼舞蹈，也意味着其飞行速度不会特别快。雄性蜉蝣i的飞行速度v的计算式为：

v=v+ae（pbest-x）+ae（gbest-x），f（x）>f（gbest）v+Dance·r            ，f（x）≤f（gbest）（2）

其中，v是蜉蝣i的第j维在第t代的速度；a，a是正吸引常数，分别用于衡量个体认知和社会认知；β是可见性系数，其取值为常数2，用来表达对其他蜉蝣的能见度；r是x和pbest的笛卡尔距离；pbest为蜉蝣i曾经到过的最好位置；r为x和gbest的笛卡尔距离；gbest为当前全局最佳位置；Dance是婚礼舞蹈系数；r是［-1，1］范围内的随机数。

蜉蝣的优秀程度定义为根据问题模型求得的适应度值，非优秀雄性蜉蝣按式（2）第1行公式更新速度，优秀雄性蜉蝣按式（2）第2行公式进行舞蹈行为吸引雌性蜉蝣产生后代来保存自身的有效信息。

笛卡尔距离计算式为：

‖x′-X‖=    （3）

其中，x′代表雄性蜉蝣i；X可指代pbest或gbest；n为蜉蝣种群的维度上限；X只在式（3）中表示雌性蜉蝣的位置。

1.2 雌性蜉蝣运动

雌性蜉蝣的运动行为与雄性并不相同，它们不成群结队，而是与雄性繁殖产生子代个体。设y是第t代的雌性蜉蝣i在第j维搜索空间中的位置，其位置更新公式如下：

y=y+v，y∈（y，y）     （4）

其中，y为初始化后位于j维的雌性蜉蝣i；y与y分别为雌性蜉蝣位置变化区域的最小值与最大值。

雌雄蜉蝣的良性结合更有助于种群的发展，优秀的雄性蜉蝣应该与优秀的雌性蜉蝣结合交配，因此算法根据适应度值对蜉蝣进行排序与配对，其数学模型为：

v=v+ae（x-y），f（y）>f（x′）v+fl·r，f（y）≤f（x′） （5）

其中，r为雌雄蜉蝣的笛卡尔距离；fl是一个随机的游动系数，当雄性比雌性优秀时，雌性的速度按式（5）第1行公式更新，当雌性不被雄性吸引时按式（5）第2行公式随机游动。

1.3 蜉蝣的交配

蜉蝣种群的发展与繁衍需要交配行为，交叉算子实现了雌雄蜉蝣之间的交配过程，具体地说，分别从雄性种群和雌性种群中按适应度选出父母样本，然后按式（6）、（7）交配产生后代：

Offspring=L·male+（1-L）·female    （6）

Offspring=（1-L）·female+L·male    （7）

其中，Offspring、Offspring分别为交叉产生的两个子代蜉蝣；L为［0，1］范围内的随机值；male为父本位置向量；female为母本位置向量。后代的初速度值设定为零。

MA算法引入高斯变异［19］，对子代蜉蝣的单个维度进行变异操作。子代蜉蝣的变异个数以种群数量Pop为基数，定义变异概率为mu，Pop·mu为种群中子代的变异个数。变异公式如下：

Offspring=Offspring+σ·N（0，1）   （8）

其中，Offspring为变异蜉蝣的第n个维度，其中n的取值为0～Pop·mu；σ为正态分布的标准差；N（0，1）为平均值为0、方差为1的标准正态分布随机数。

2 S-AMA的改进思想

由于蜉蝣算法的全局搜索能力较弱，交配后产生的优秀子代蜉蝣直接进行下一代的迭代，对子代优秀个体有效信息的利用不够充分，导致算法在计算中后期易陷入局部收敛，影响了算法的优化效果。为了克服上述缺陷，笔者提出S-AMA算法，着重加强种群的全局搜索能力，并在算法后期的优秀子代蜉蝣中加入稚虫迁徙机制，利用稚虫寻找富氧栖息地的能力跳出局部极值，避免了算法早熟收敛。

2.1 基于Logistic混沌映射的初始化方法

混沌序列具有内随机性、遍历性、规律性等特点，看似混乱却有着精致的内在结构，由混沌序列搜索得到的初始群体在一定程度上能够提高算法的搜索效率［20］，增加种群多样性。种群多样性是元启发式算法寻得最优解的基本前提。混沌序列的生成方式主要有5种混沌映射［21］：Logistic映射、Henon映射、Tent映射、Lorenz映射、逐段线性混沌映射。由于Logistic映射从数学形式上是一个相对简单的映射方法，且其混沌系统具有不错的安全性，因此经常被用作设计混沌流密码系统。综上所述，S-AMA利用Logistic混沌映射的数学特性产生初始种群，可使初始种群在解空间内分布得更加均匀、随机，有助于提升算法的种群多样性，而初始种群的丰富有利于算法更加全面地探索，提高最终优化解的精度。具体而言，笔者提出的初始化方法可以使初始种群在解空间内分布的点位更加均匀、随机，算法基于映射后的点位能够更加充分地探索最优解。Logistic混沌映射的数学公式为：

z=μ·z（1-z），μ∈［0，4］，z∈［0，1］   （9）

其中，z为第n+1代蜉蝣i的混沌映射位置；μ为分支参数，通常取4；z为第n代蜉蝣i的混沌映射位置。

把式（9）中的z代入式（10）可得种群初始化计算式：

x=x+z（x-x）    （10）

其中，x为初始化过程中的第i个蜉蝣的位置。

2.2 基于S型生命系数的自适应惯性权重系数

文献［9］提出一种对基础蜉蝣算法的改进方法，加入了重力系数因子g（相当于一种惯性权重因子），在算法的搜索与开发能力上具有平衡与指导的作用。

雄性蜉蝣的速度更新公式如下：

v=g·v+ae（pbest-x）+ae（gbest-x），f（x）>f（gbest）g·v+Dance·r          ，f（x）≤f（gbest）

（11）

雌性蜉蝣的速度更新公式如下：

v=g·v+ae（x-y），f（y）>f（x）g·v+fl·r    ，f（y）≤f（x）  （12）

当惯性系数较大时算法探索能力较强，而当惯性系数较小时算法的开发能力较强［22］。MA的重力系数权重随着算法迭代逐渐呈线性减少，没有针对性地对种群前期的探索进行着重处理，也没有对后期的开发进行适应调整，影响了算法的搜索性能。

本研究将S型生命系数看作蜉蝣的生命能量，前半生青壮年蜉蝣的精力充沛能够飞行到更广泛的区域进行全局搜索，到了后半生暮年之际具有丰富的经验能够更加精准地进行局部搜索。如图1所示，如果把惯性权重因子看作蜉蝣的生命能量，S型生命系数可以使算法在迭代前期具有较大的惯性系数，更好地进行全局搜索；而在迭代后期急速下降并保持一个较小的值，使算法倾向于局部搜索。笔者提出的S型生命系数可以很好地平衡算法的全局搜索能力与局部搜索能力，满足算法各个阶段的需求［23］。Sigmoid函數是基础的S型激活函数，故在此引入的S型生命曲线为Sigmoid函数（图1）。

图1 符合S型生命曲线函数

第t代的生命曲线系数ω的计算式为：

ω=ω+（ω+ω）/（1+exp（-（2S·（T-t）/T-S）））（13）

其中，ω与ω为惯性权重的最大值与最小值，分别为0.8与0.2；T为最大迭代次数；t为当前的迭代次数。本研究选取［S，S］范围内S型生命曲线的自适应系数函数，其中S为10，S为-10。

综上所述，带有S型生命曲线自适应系数的雄性蜉蝣的位置更新公式如下：

v=ω·v+ae（pbest-x）+ae（gbest-x），f（x）>f（gbest）ω·v+d·r            ，f（x）≤f（gbest）

（14）

带有S型生命曲线自适应系数的雌性蜉蝣的位置更新公式如下：

v=ω·v+ae（x-y），f（y）>f（x）ω·v+fl·r    ，f（y）≤f（x）  （15）

2.3 蜉蝣的稚虫迁徙机制

蜉蝣稚虫在生长发育过程中，要不断蜕皮，并且稚虫在缺氧条件下能够移动到更多氧环境的栖息地生活。在此现象启发下，本研究利用父母蜉蝣交配产生基因优秀的子代蜉蝣，根据优秀子代蜉蝣在稚虫期寻氧迁徙活动，自主地从缺氧环境迁移到氧气充沛的环境中，寻找更适宜的栖息地。S-AMA稚虫迁徙公式如下：

OffSpring=OffSpring+m·（Levy·gbest-OffSpring） （16）

其中，OffSpring为第t代的稚虫i的位置；m为迁徙系数，控制种群四处寻找有氧环境的能力，取［0，1］范围内的随机数；Levy为莱维飞行；gbest为目前蜉蝣所能到达的最优位置，即当前全局最优位置，因为不光是稚虫迁徙机制在更新位置，还有雌雄蜉蝣各自在更新位置，所以只说稚虫寻到氧气最充沛的位置不全面。

稚虫通过向氧气充沛的地方靠近，来寻找更加合适的栖息地。莱维飞行能够增加稚虫群体迁徙的范围，使其能在目前最适合的位置周围扰动，增加寻找到最优栖息地的概率。通过式（16）的应用，子代能够进一步提升自己的优秀度，增加寻优精度，提高跳出局部最优的可能性。

莱维飞行是模拟自然界中一种鸟类飞行的运动，它和随机游走的布朗运动不同，拥有小概率大步伐、大概率小步伐的特征，能够使种群在后期进化中既拥有较好的局部寻优能力又同时拥有强力跳出局部最优值的能力［24］。莱维飞行的运动可表示为：

Levy=γ·     （17）

σ=（18）

其中，γ为莱维飞行的飞行尺度；u，v是（0，1）内的随机值；β′是莱维飞行中的默认常数，设置为1.5；J（）为伽玛函数；σ为标准差。

2.4 算法时间复杂度分析

对于MA算法来说，设搜索空间维度为D，雄性蜉蝣数量为N，雌性蜉蝣数量为N，子代蜉蝣交配数量为N，交配过程的复杂度记为O（N）。最大迭代次数为T。初始化过程的复杂度为O（1），标准MA的时间复杂度T（n）=O（1+T（ND+ND+ND））。

S-AMA增加了混沌初始化、S型生命系数自适应惯性权重和稚虫迁徙机制。混沌初始化与S型生命系数自适应惯性权重都分别嵌入在初始化与速度更新公式中，所以复杂度都为O（1），加入稚虫迁徙机制，增加了对子代蜉蝣的进化公式，使其进行迭代更新，其复杂度为O（N）。则过滤低次项后改进的算法时间复杂度为 T（n）=O（1+T （N D+N D+N （D+1）），可以看出，算法改进后，并未明显提升时间复杂度。

3 實验分析与性能评估

为了验证S-AMA算法的性能，采用标准测试函数进行实验。实验环境采用Intel（R）Core（TM）I5-10th CPU，内存8 GB，操作系统为64位WIN11计算机。编程语言MATLAB（R2020b）。使用23个标准测试函数［25］对S-AMA进行性能测试，详见表1，在这些函数中，F1～F7为单峰函数，仅有一个全局最优解，用来测试算法的局部开发能力和收敛速度；F8～F13为多维度多峰函数，具有多个局部最优值和一个全局最优值，用来测试算法的全局搜索能力与跳出局部最优的能力；F14～F23为固定维数的多峰测试函数，用来检测算法平衡探索与开发能力之间的性能。

3.1 对比算法与参数设置

本次选择6种算法进行对比，其中有针对MA的最新改进算法IVMA［14］、LMA［13］，性能较为优秀并且较新的群启发式算法HHO［6］、GWO［8］，以及传统群优化算法PSO［4］。为了更加直观有效地对比各算法的优劣，设定参数尽量统一，种群规模N=50，维度D=30，最大迭代次数Tmax=500，其他参数设置见表2。各算法独立运行30次，选取平均值、标准差、最优值、Wilcoxon秩和检验作为评价标准，其中平均值与标准差越小算法性能和稳定性越佳。

3.2 求解精度分析

S-AMA及对比算法的实验结果见表3，其中Best为最优适应度值、Mean为平均值、Std为标准差，红色数据是最佳实验结果。F1～F7为单峰函数。可以看到S-AMA在F1～F4中都能达到最好的寻优结果以及寻优精度，在F5～F7中寻优结果也位于前三；在F8～F13的多峰函数中，S-AMA在大多数情况下都找到了最优值，仅在F10中稳定性稍弱于HHO，但也寻到了最优值，可见S-AMA具有优秀的跳出局部最优能力和探索能力，整体效果最优。对于其他多峰固定维度函数，除了函数F23的标准差没有达到最优，其余皆为最优，充分说明S-AMA算法具有突出的平衡探索与开发能力，能在寻到最优的基础上保持最佳的稳定性。

3.3 收敛曲线分析

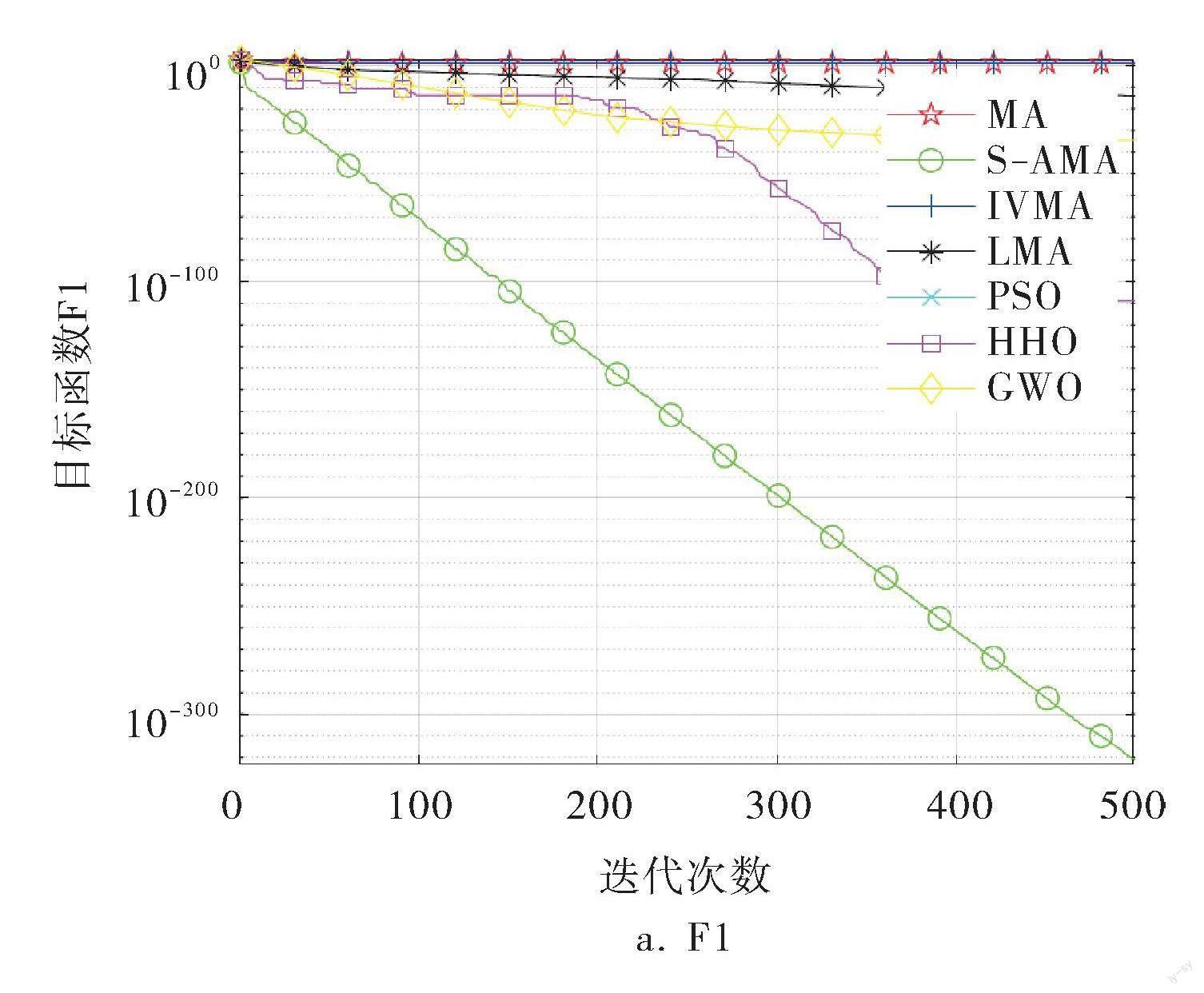
各种算法的部分函数收敛曲线如图2所示，从中可以更加直观地看出差异性。在单峰测试函数F1～F4中，可以看到S-AMA的寻优精度远远强于其他所有算法，仅在F3中，S-AMA在中期收敛略慢于HHO，但到迭代后期，收敛精度远优于HHO；而在多峰测试函数F8～F11中可以看到，S-AMA能够以极快的速度收敛到最优值，远远超出其他函数的效率，仅在F10中，寻优精度略逊于HHO；而在F13中，也是在后期拥有了最好的寻优精度。通过图像收敛曲线（图2）可以看到，S-AMA的初期收敛速度远胜于其他算法，说明引入的混沌映射产生的种群多样性对于算法的前期探索奠定了良好的种群基础；到了后期，曲线持续下滑，则是由于引入的S型生命曲线以及稚虫迁徙机制发挥了不错的效果。从收敛曲线分析可知，3种改进策略对算法的优化都有不错的效果。

图2 各种算法的部分函数收敛曲线

综上所述，S-AMA在寻优速率与寻优精度上综合强于其他算法。

3.4 Wilcoxon秩和检验

为了精确分析实验结果，采用Wilcoxon秩和检验来检验算法结果之间是否具有显著性差别。秩和检验在5%的显著水平下进行，当检测值p＜0.05时，可以证明两种算法的性能存在着显著差异，否则证明两种算法的寻优性能并没有显著差异。

将S-AMA算法与要对比的6种算法各自独立运行30次，参数种群个数N=30、维度D=30，测试23个标准测试函数判断S-AMA与6种对比算法所得结果的显著性区别。Wilcoxon统计的检验值p见表4，其中，红色数据表示算法间差异性较小，性能相当；N/A表示数据无效，即实验样本数据相同，算法性能相当。根据p值判断，当p＜0.05时，说明所对比的两种算法有显著性差异。表4中的红色数据表示算法之间没有显著性差异，仅出现很少的次数，表明S-AMA与其余对比算法之间在绝大部分情况下均具有显著性差异。

综合分析表3、4和图2可知，具有稚虫迁徙机制的自适应混沌蜉蝣优化算法（S-AMA）的全局和局部寻优能力都得到加强，寻优能力优于MA以及IVMA、LMA和PSO，并且也优于性能优良的较为新颖的HHO、GWO。说明S-AMA具有优秀的收敛精度、收敛速度和鲁棒性。

4 结束语

笔者提出一种具有稚虫迁徙机制的S型自适应混沌蜉蝣优化算法。改进后的蜉蝣算法经过标准函数的测试后，有效证明了其收敛速度和收敛精度有所提升。蜉蝣算法目前已经能够应用到动态网络社区发现问题，以及线性天线阵列的模式合成优化等问题中，算法整体性能的提升，可进一步提高蜉蝣算法在工程优化领域中应用的可能性。然而算法性能的进步总是伴随着稳定性的下降，改进后的蜉蝣算法若想要真正融入且扩散到各个领域，仍然需要研究在保证算法寻优稳定性的前提下提高算法整体的寻优性能，尽可能降低其优化误差。因此，下一步的研究方向应该使用不同的现实数据集来测试改进的蜉蝣算法，继续发现其优缺点，逐步改进，使其尽可能完善，并最终应用到各领域中，发挥其价值。

参 考 文 献

［1］ 张发展，贺毅朝，刘雪静，等.新颖的离散差分演化算法求解D{0-1}KP问题［J］.计算机科学与探索，2022，16（2）：468-479.

［2］ QIAN N.On the momentum term in gradient descent learning algorithms［J］.Neural Networks，1999，12（1）：145-151.

［3］ 孙秋野，陈会敏，杨家农，等.牛顿类潮流计算方法的收敛性分析［J］.中国电机工程学报，2014，34（13）：2196-2200.

［4］ 李浩，楊海潇，张兰，等.改进离散蜉蝣算法的多目标动态网络社区发现［J］.计算机科学与探索，2023，17（4）：942-952.

［5］ NAIK M K，PANDA R，ABRAHAM A.Normalized square difference based multilevel thresholding technique for multispectral images using leader slime mould algorithm［J/OL］.Journal of King Saud UniversityComputer and Information Sciences，［2021-02-04］.https：//doi.org/10.1016/j.jksuci.2020.10.030.html.

［6］ XIA K W，WANG T，ABUBAKAR U.Pattern Synthesis of Uniform and Sparse Linear Antenna Array Using Mayfly Algorithm［J］.IEEE Access，2021（9）：77954-77971.

［7］ LIU Z K，JING P，WANG J Z，et al.Ensemble forecasting system for short-term wind speed forecasting based on optimal sub-model selection and multi-objective version of mayfly optimization algorithm［J］.Expert Systems with Applications，2021，177：114974.

［8］ KENNEDY J，EBERHART R.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Piscataway，NJ：IEEE，1995：1942-1948.

［9］ ZERVOUDAKIS K，TSAFARAKIS S.A mayfly optimization algorithm［J］.Computers & Industrial Engineering，2020，145：106559-106577.

［10］ HEIDARI A A，MIRJALILI S，FARIS H，et al.Harris hawks optimization：Algorithm and applications［J］.Future Generation Computer Systems，2019，97：849-872.

［11］ LI S M，CHEN H L，WANG M J，et al.Slime mould algorithm：A new method for stochastic optimization［J］.Future Generation Computer Systems，2020，111：300-323.

［12］ MIRJALILI S，MIRJALILI S M，LEWIS A.Grey wolf optimizer［J］.Advances in Engineering Software，2014，69：46-61.

［13］ OLPERT D H，MACREADY W G.No free lunch theorems for optimization［J］.IEEE Transactions on Evolutionary Computation，1997（1）：67-82.

［14］ 陈嘉豪，童楠，符强.基于Logistic映射的蜉蝣优化算法［J］.计算机时代，2021（10）：6-10.

［15］ 陈伟超，符强.基于倒位变异的蜉蝣优化算法［J］.计算机系统应用，2021，30（8）：157-163.

［16］ 王义，张达敏.基于黄金正弦与自适应融合的蜉蝣优化算法［J］.计算机应用研究，2021，38（10）：3072-3077.

［17］ 王克逸，符强，陈嘉豪.偏移进化蜉蝣优化算法［J］.计算机系统应用，2022，31（3）：150-158.

［18］ 王义，张达敏，邹诚诚.增强全局搜索和自适应蜉蝣算法［J］.哈尔滨工业大学学报，2022，54（11）：137-150.

［19］ SHAO D，XU S C，DU A M.Dynamic friction modelling and parameter identification for electromagnetic valve actuator［J］.Journal of Central South University，2018，25（12）：3004-3020.

［20］ 闫乐乐，李辉.基于复合混沌序列的动态密钥AES加密算法［J］.计算机科学，2017，44（6）：133-138.

［21］ 张诣.Logistic混沌映射［J］.电脑知识与技术，2008，35（4）：2538-2539.

［22］ SHI Y，EBERHART R.A modified particle swarm optimizer［C］//1998 IEEE International Conference on Evolutionary Computation Proceedings.Piscataway，NJ：IEEE，1998：69-73.

［23］ 路復宇，童宁宁，冯为可，等.自适应杂交退火粒子群优化算法［J］.系统工程与电子技术2022，44（11）：3470-3476.

［24］ RAMBABU M，BHOOKYA N.GMPPT by using PSO based on Levy flight for photovoltaic system under partial shading conditions［J］.IET Renewable Power Generation，2020，14（7）：1143-1155.

［25］ YAO X，LIU Y，LIN G M.Evolutionary programming made faster［J］.IEEE Transactions on Evolutionary Computation，1999（3）：82-102.

（收稿日期：2023-05-16，修回日期：2023-05-26）

S-type Adaptive Mayfly Algorithm Based on Larval Migration Mechanism

ZHANG Heng-qia，b， QIAN Qiana，b

（a. Faculty of Information Engineering and Automation；  b. Yunnan Key Laboratory of Computer

Technology Applications ， Kunming University of Science and Technology ）

Abstract   Considering Mayfly algorithms（MA） poor searching ability， shortcomings in the individual information utilization of excellent offspring and the troubles to fall into local convergence in the middle and late calculation which affects the optimization effect， S-type adaptive mayfly algorithm based on larval migration mechanism （S-AMA） was proposed to solve above problems. Firstly， the S-AMA has Logistic chaotic mapping used to initialize both male and female mayfly populations and increase the diversity of the populations. Secondly， it has the Mayfly life cycle modeled and the S-type life coefficient added to replace the original gravity inertia coefficient to dynamically adjust the balance between the exploration ability and development ability of the algorithm； finally， through considering the life cycle in oxygen-deficient environment of a mayfly， a larval migration mechanism was introduced to strengthen the ability of the superior offspring to get out of local optimum and improve the convergence accuracy of the algorithm so as to enhance the convergence accuracy of the algorithm and search the region near the optimal solution more fully. In the experimental part， S-AMA was applied to the standard function test set， and the optimization contrast experiment and Wilcoxon rank sum test were performed respectively. The results show that the S-AMA algorithm has better optimization ability， convergence speed and robustness than the comparison algorithms. In the experiment， making use of standard function test set to compare the searching ability of the S-AMA with some other algorithms and implement the Wilcoxon rank sum test shows that， as compared to the contrast algorithm， the S-AMA has good optimization ability， convergence speed and strong robustness.

Key words   S-AMA， larval migration mechanism， chaotic mapping， S-type life coefficient， Levy flight