基于改进AFSA算法的智慧农业监测网络研究
2024-04-25闫好明
闫好明,刘 洋
(南阳农业职业学院,河南 南阳 473000)
智慧化农业生产主要通过数据采集、传输、处理、调控等智慧化手段来实现资源合理利用、生产成本降低、产量与品质提高的目标。其实现方法一般是利用传感器与嵌入式技术,采集农业生态环境相关数据,通过无线通信技术将收集到的数据经过网关传给服务器平台,实现数据的智能采集和农业环境变量科学调控[1]。在智能农业生产监测过程中,需要处理的一个重点就是如何根据实际情况选择合适的优化策略,把传感器节点部署到所监测的农业范围内,以最大限度增加覆盖率或减少节点数量,从而提高监控区域的网络服务质量。人工鱼群算法在全局情况下寻优能力更强,对于初值的要求不高且易于实现,能较好地解决农业监测环境下的网络覆盖问题[2],但视野固定会使算法后期收敛缓慢,易陷入局部最优,需要进一步优化。本文针对农业监测环境下无线传感器网络最优覆盖问题,提出了一种改进型人工鱼群算法,并通过覆盖问题仿真分析其可靠性。
1 人工鱼群算法
人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)是一种自上而下的新型寻优方式,由我国学者李晓磊于2003年提出,是集群智能思想的具体应用,具有全局范围内收敛性好、对初始值要求小等优势[3]。鱼通常可以自己去找,或者跟着其他鱼去寻找水中食物丰富的区域。因此,在寻找到的这个水域中,鱼通常是最多的,而且食物也是最丰富的。人工鱼群算法就是利用鱼类寻求食物浓度最高水域的这一特征,构造个体模型,模拟鱼群在水中觅食、聚集、追尾及随机这4种基本行为。鱼类的这4 种行为都与寻找最优问题的求解密切相关,如何以一种简单而有效的方式来构建和实现这些行为求取最优解,将是算法应用中需要思考的关键问题。
2 农业监测网络覆盖问题模型建立
2.1 传感器模型选择
传感器节点的监测模型体现了提供覆盖的节点的感知能力,是研究网络覆盖控制的基础[4]。由于传感器节点在各种应用环境中的功能和物理特性具有多样性,难以对传感器节点进行统一描述,所以采用布尔感知模型作为传感器模型,该模型是将传感器节点覆盖问题理想化。如果待监测信息点与传感器节点之间的欧式距离小于传感器可监测半径,则认为该信息点在节点可监测范围内,该信息点被节点监测到的概率为1,否则设为0。因此,布尔感知模型又可称为二进制感知模型[5]。
布尔圆盘模型为理想传输环境下的节点感知模型,也叫全向感知模型。在无线传感器网络布置的二维平面上,以节点S为圆心,以Rs为半径的圆形为节点的传感覆盖范围。由于模型简单实用,所以常用来分析传感网络的覆盖性能。
节点S的坐标假定为(x0,y0),传感半径Rs,任意目标点Q的坐标(x,y),S与Q之间的欧式距离为d,则圆盘模型的覆盖函数如式(1)所示,模型表示如图1所示。
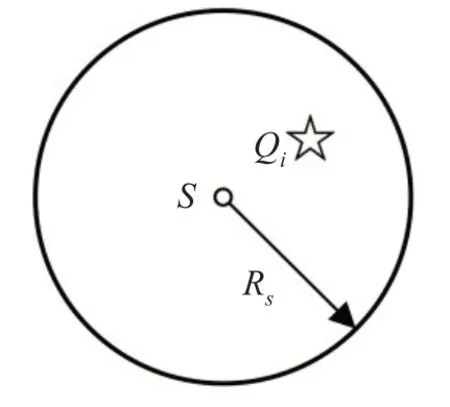
图1 布尔圆盘模型(全向感知模型)Fig.1 Boolean disk model(omnidirectional perception model)
2.2 网络覆盖模型
由于农业监测环境的确定性,所以对网络覆盖问题分析采用网格化办法。传感器节点采用布尔感知模型,如果网格点与传感器节点之间的欧式距离小于传感器可监测半径,便认为该网格点可以被节点监测到[6]。当监测环境中的全部网格点都可以被至少一个节点监测到时,该农业监测网络可以覆盖整个农业待监测区域,获取区域范围内的全部环境信息。
在节点有移动能力的情况下,通过预先设定的算法实现节点对网络的自组织和自适应部署。利用随机、确定或移动的方式,传感器网络可以在监测区域内分布节点。节点的可移动性分为两类,一类是所有节点都可以移动,节点能量消耗较大;另一类是在固定网络中增加一定数量可移动节点,以增强固定无线传感器网络的覆盖和节点间的连接,从而提高网络的覆盖性能。
2.3 农业监测网络覆盖问题模型建立
在农业环境下,监测范围A是一个二维平面,将其划分成单位长度为1 的(m×n)个网格,在此区域内投放参数设置相同的移动传感器节点。设传感器数目为N,有效监测半径均为RS,则传感器节点集可以表示为S{S1,S2,S3,...,SN},其中Si={xi,yi,RS},表示以节点坐标(xi,yi)为圆心,以RS为半径的监测圆。将目标Q(x,y)被传感器节点Si所能监测到的事件定义为Hi,则事件发生的概率P{Hi}即为目标点(x,y)被传感器节点Si所覆盖的概率Pcov(x,y,Rs)。
当目标点(x,y)到节点的距离小于传感器有效监测半径RS时,就认为该目标点在传感器节点覆盖范围,可以被该节点监测到并收集相关数据。故Pcov()x,y,Rs也可称为节点RS对目标点Q的感知度。
在节点集中只要有一个传感器节点可以监测到目标点(x,y)的信息,就可以认为该目标点被节点集所覆盖。因此,目标点被节点集所覆盖的概率为Hi的并集,假设所有的随机事件Hi是相互独立的,则传感器节点集S的覆盖率如下:
监测范围A数字离散化后共m×n个像素,用Δx×Δy来表示每个像素的面积,假设其面积为1。每个像素能否被有效监测用节点集覆盖率Pcov()x,y,Rs来衡量,则将节点集S的区域覆盖率Rarea( )S定义为节点集S的覆盖面积Aarea( )S与监测区积As之比,即为:
最终目标就是在监测范围内找到一组最优的节点分布使得覆盖率最大。
3 基于改进AFSA算法的覆盖问题仿真
3.1 基本人工鱼群算法改进
传统人工鱼群算法虽然对于初值和参数设定要求不高,但由于鱼类个体视野和步长的选择具有随机性,搜索精度难以提高,所以算法收敛速度减慢。由于鱼群聚集愈多,鱼食浓度愈高,所以当前范围内最优值的结果是以最优解域临近范围内鱼群聚集较多的中心为目标。根据鱼群活动情况的不同,聚集中心会不断变化,故在算法迭代时,可能受到局部最优值干扰,忽略最优解。因此,需要对其进行改进来达到寻优精度更高、算法收敛速度更快、更加适合实际应用的目的。
设鱼类个体的当前状态信息为X=(x1,x2,…,xn),探索下一个状态信息为Xv=(x1v,x2v,…,xnv),其表示公式如下:
求极值问题时可表示为:
式中:Rand()为随机数产生函数,Rand() ∈(0,1);Step为可移动步长;Yv为Xv目标函数值;Y为X状态的目标函数值。
当前鱼类个体的状态信息和视野中目标点的状态信息决定了算法中的移动步长。
3.2 改进人工鱼群算法执行
步骤1:结合无线传感器网络环境、传感器节点参数等,对人工鱼群的参数进行初始化设置,主要包括种群规模即传感器节点个数N、鱼类个体视野即传感器节点可监测范围Visual、移动步长即传感器节点可移动范围Step、拥挤度因子δ、重复次数即每个节点移动尝试次数Try_number,设置变异因子pm、最优人工鱼状态变化次数keepTimes,视步系数a,最大迭代次数值MAXgen,公告板。选取农业监测区域范围,在其范围内随机生成N条人工鱼坐标信息。
步骤2:结合式(6),计算鱼群算法中各个个体当前状态的食物浓度值即农业监测网络覆盖率的值,用Yavg、Yi来表示。并在公告板中记录最小的Yi值和当前人工鱼的状态信息。
步骤3:对鱼类个体执行觅食、聚群、追尾等三种基本活动的状态信息和目标函数结果进行评价比较,判断当前个体值Yi是否≥鱼群整体值Yavg,若是则执行步骤4 适应选择视野,否则以初始化视野转到步骤5,继续执行。
步骤4:测量每条人工鱼自身到其他人工鱼的距离,并求出平均值结合视步系数a确定传感器节点即鱼类个体的监测范围和可移动区间,继续执行步骤5。
步骤5:对比传感器节点视野范围内的目标函数值,若优于公告板中值则以自身状态取代,并将keep-Times值设为0,转到步骤7 继续执行;不然keepTimes+1,判断keepTimes值是否已达到MAXbest,若是则执行步骤6,否则转到步骤7执行。
步骤6:查找目标函数值较差的全部人工鱼即传感器节点位置信息,对每个传感器节点生成随机数值Rand(1),Rand(1)∈(0,1)。若Rand(1)>pm,则用pm对其进行变异,即用历史最优节点状态来替换该节点状态。直到所有具有较差目标值的个体替换完成,令keepTimes=0;否则传感器节点状态信息保持不变;继续执行步骤7。
步骤7:在上述步骤基础上,对于覆盖问题模型不断迭代求解,计算鱼类个体最佳分布信息值和所求目标函数值。当其迭代次数达到设定最大值时,则判断算法求解结束,并在公告牌中更新并输出当前传感器节点的分布信息和覆盖率最大值。反之则不断进行迭代过程,每次次数加1,直到达到设定最大值为止。
4 覆盖问题仿真
4.1 基本AFSA算法仿真覆盖分析
在MATLAB R2020a 平台进行覆盖问题模型的仿真,设农业监测环境目标区域范围为50 m×50 m,节点可监测半径为5 m,传感器节点数目为35 个,最大迭代次数为200次,鱼类个体的视野为5 m,个体最大尝试次数为10 次,拥挤度因子为0.618。初始情况下,将传感器节点任意抛洒在监测区域内,在仿真软件中模拟其分布情况和覆盖效果。传感器节点随机分布情况如图2所示。

图2 AFSA-WSN节点初始分布Fig.2 Initial distribution of AFSA-WSN nodes
在上述仿真环境条件下,采用基础人工鱼群算法对农业监测节点覆盖问题进行仿真求解。对图2 中初始条件下传感器节点的随机分布位置进行优化后,最终得到的节点分布和覆盖效果如图3 所示。对比图2和图3可以看出,采用人工鱼群算法对传感器节点分布进行优化后,节点分布更加均匀合理,覆盖程度大,对于目标区域所需数据的监测更加完整。结合输出结果可以看出,随着迭代次数的增加,节点覆盖率由初始69%左右增加到88%,达到大幅度提升。
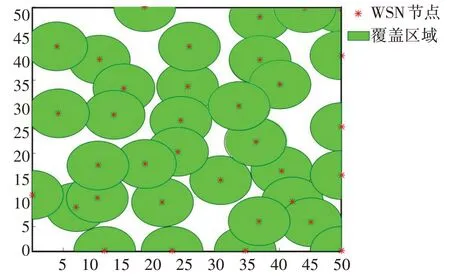
图3 人工鱼群算法优化后传感器节点分布情况Fig.3 Distribution of sensor nodes after optimization by artificial fish swarm algorithm
4.2 改进AFSA算法仿真覆盖分析
改进后的人工鱼群算法对传感器节点网络覆盖优化效果如图4、图5所示。对比图3可以看出,改进后的算法使传感器节点在监测区域内的分布位置更加合理均衡,而常规人工鱼群算法求解结果存在许多重复覆盖区域,覆盖盲区也比较多。

图4 改进AFSA-WSN传感器节点初始分布情况Fig.4 Improvement of the initial distribution of AFSA-WSN sensor nodes
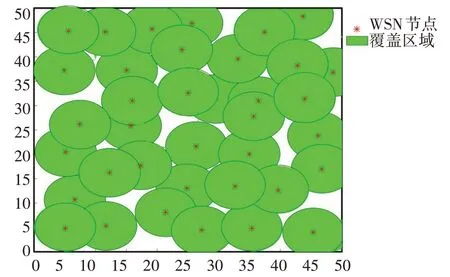
图5 改进AFSA-WSN最终传感器节点分布情况Fig.5 Improvement of the final sensor node distribution of AFSA-WSN
对比了在相同的仿真环境和基本参数设置情况下,常规鱼群算法和改进后算法针对农业监测网络覆盖问题的优化迭代过程。对比最终优化结果,常规人工鱼群算法在200 次迭代后监测系统对于目标区域的覆盖率约为88%,而改进后的鱼群算法的覆盖率达到97%以上,如图6 所示。此外,改进后的人工鱼群算法收敛速度更快,由此可见改进人工鱼群算法更好地实现对农业监测网络覆盖问题的优化。通过观察优化后的节点分布情况可知,相较优化前的基本算法,其在监测区域内的分布更为合理,节点利用率更高。将两种算法仿真结果经20 次统计后取平均值,对照情况如表1 所示。从中可以看出,在相同迭代次数下,改进后的人工鱼群算法能取得更高的覆盖率,说明其求解速度更快、效果更优。
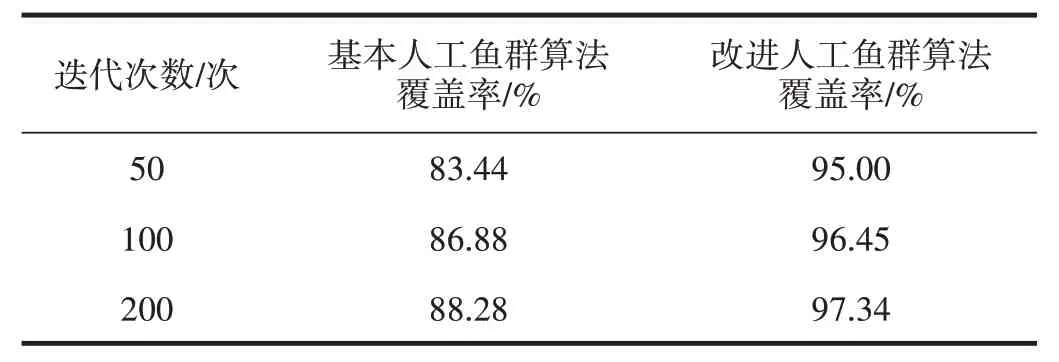
表1 改进AFSA算法与AFSA算法仿真结果对比(20次统计)Tab.1 Comparison of simulation results between improved AFSA algorithm and AFSA algorithm(20 statistics)
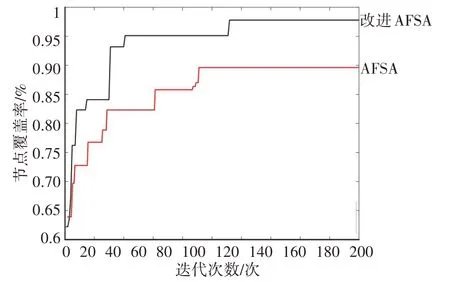
图6 改进AFSA与AFSA算法优化过程对比Fig.6 Improvement of the AFSA and AFSA algorithm optimization process comparison
5 结语
针对无线传感器网络节点的覆盖问题,本文采用传统人工鱼群算法和改进人工鱼群算法进行了优化研究,以实现网络传感器应用的高覆盖率。将人工鱼群算法思想应用到农业环境监测覆盖方面,提出了具体的求解步骤,并通过MATLAB 仿真软件进行了验证。根据传统人工鱼群算法中存在的不足,提出了改进方法和求解步骤,并将MATLAB 仿真结果与基础人工鱼群算法和经典智能优化算法相对比,证明了改进后的方法更优。
